ПАРОИЗОЛЯЦИОННЫЕ МАТЕРИАЛЫ
БИТУМ МАТЕРИЛЫ С НЕОРГАНИЧЕСКОЙ БЕЗОСНОВНЫЕ - легкоплавкие до 50С (НЕГНИЮЩЕЙ) ОСНОВОЙ МАТЕРИАЛЫ - (коэф. теплопроводности 0.35) (гидрозол- асбестовый картон, (изол, бризол-
БИТУМНЫЕ наружных покрытий толщина 1мм, прокатыванием МАТЕРИАЛЫ С ОРГАНИЧЕСКОЙ фольгоизол- алюминиевая фольга через вальцы ОСНОВОЙ (пергамин- кровельный толщиной 0.2 мм покрывается смеси нефтяных картон,пропитанный легкоплавким с одной стороны битумно-резиновым битумов с напол- битумом с толщиной листов 0.5мм составом толщина листов 4мм, нителем в виде рубероид- кровельный картон, стеклорубероид, стеклозол- основа асбестовых волокон пропитанный легкоплавким стекловолокнистая ткань, на которую и талька и с дроб- битумом и с двух сторон наносят битум или битумно-резиновую ленной резиной. покрытый слоем тугоплавкого массу, толщина листов 2-3 мм) Толщина –2мм, бутума, толщина 1.5мм, отличаются коэффициент паропроницаемости высокой - 0.3760) пластичностью при низких темп.
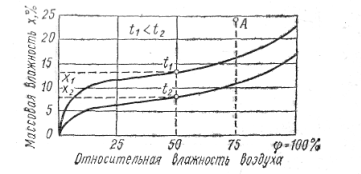
Теплоизоляционные органические материалы - пленочно – сотовый материал - пенопласт полистирольный - пенопласт фенолформальдегидный - пенопласт пенополиуретановый - пенопласт поливинилхлоридный - пробковые плиты - рипор - рукав гибкий изолирующий - торфяные плиты - феноформалит - фласт - плиты лигноперлитовые Теплоизоляционные неорганические материалы - АТМ-1 теплоизоляционный материал - керамзит - Плиты жесткие минераловые - газобетон - морские плиты - пенобетон - пеностекло - перлит высушенный - перлитобитумные плиты - перлитофосфогелевые плиты - стекловата - шлак 20. Увлажнение материалов в ограждающих конструкциях. Формы связи влаги с пористыми телами. Основные уравнения, описывающие процесс увлажнения материалов. Характер графиков t х , Pх, Pх’’, φх, x в однородных и неоднородных ограждениях. Поглощение влаги материалом ведет прежде всего к ухудшению тепловых свойств материала. Объясняется это тем, что вода может занимать в материале часть объема ячеек и пор, вытесняя из них газ. Так как теплопроводность воды λw — 0,58 (Вт/мК) примерно в 25 раз больше теплопроводности неподвижного воздуха, то наличие воды в материале вызывает существенное повышение теплопроводности теплоизоляционного материала. При низких температурах вода в порах материала может замерзнуть, что приведет к еще большему возрастанию теплопроводности материала, так как теплопроводность льда λл = 2,2 Вт/(мК) почти в 100 раз больше теплопроводности неподвижного воздуха. Зависимость теплопроводности материала от объемной влажности может быть выражена эмпирической формулой λ;, = λ;с.м + Δ λ*w где λ;с.м — коэффициент теплопроводности материала в воздушно-сухом состоянии. Δ λ; — приращение коэффициента теплопроводности на каждый процент увеличения объемной влажности; w — объемная влажность, %. Величину Δ λ; органических материалов при положительных температурах принимают равной 3,5*10-3, а при отрицательных температурах 4*10-3 Вт/(мК); неорганических материалов— соответственно 2,3*10-3 и 3,5*10-3 Вт/(мК). Содержащий влагу изоляционный материал может подвергаться гниению, в нем могут образовываться грибки и плесени, что приводит к разрушению материала и сокращению срока его службы. По классификации академика П. А. Ребиндера, все формы связи капиллярно-пористых тел с поглощенной влагой делятся на три большие группы: 1) химическая связь; 2) физико-химическая; 3) физико-механическая. Химическая связь характеризуется наибольшей прочностью и совершенно точными соотношениями между количествами сухого материала и присоединенной влаги, не изменяющимися при изменении внешних условий. Присоединение воды происходит в процессах гидратации и кристаллизации (образование кристаллогидратов). Химически связанная влага не удаляется даже при нагревании материала до 120—150° С. Формам физико-химической связи свойственны различные, но определенные соотношении между количествами сухого материала и влаги, соответствующие условиям внешней среды. Из форм физико-химической связи наибольшее значение имеет адсорбционно-связанная влага (гигроскопическая влага). Поступление гигроскопической влаги в материал и ее продвижение в материале происходит в парообразном состоянии. Формы физико-механической связи еще менее прочные, и им соответствуют неопределенные соотношения между количествами сухого материала и поглощенной воды, которые, однако, могут иметь предельные значения. Поглощение влаги при таких формах связи происходит при непосредственном соприкосновении материала с капельной влагой. Влагой в формах физико- механической связи являются капиллярная влага, перемещающаяся в микро- (r < 0,1 мкм) и в макрокапиллярах (r > 0,1 мкм), а также влага смачивания, удерживающаяся в порах материалов в результате прилипания воды к стенкам оболочек пор. Обе формы физико-механической связи вызваны наличием поверхностного натяжения у жидкостей. Содержание влаги в материале в состоянии равновесия приобретает некоторое постоянное значение, называемое равновесной гигроскопической влажностью или равновесной влажностью материала. Материалы, имеющие значительную равновесную влажность, называются гигроскопичными. Равновесную влажность материалов определяют опытным путем после выдержки (в течение 1 сут) образцов в атмосфере влажного воздуха различной установленной влажности, Результаты опытов изображаются графически в виде кривых равновесной влажности или изотерм сорбции влаги (рис. 3.3), поскольку процесс сорбции обычно исследуется при постоянной температуре. Ордината любой точки кривой дает величину равновесной влажности материала, соответствующей данной влажности воздуха. Равновесная влажность материала, отвечающая насыщенному воздуху, называется максимальной гигроскопической влажностью. Область в диаграмме выше кривой равновесной влажности является областью капиллярной влажности. Если, например, при t1 и влажности воздуха φ = 75% материал имеет влажность, определяемую ординатой точки А, то можно утверждать, что в материале имеется еще и капиллярная влага. Равновесная влажность материала убывает с повышением температуры (x2<; x1).__
рх = рн-(w/μ)δх (3.11а) Пренебрежение сопротивлением влагопереходу позволяет принимать парциальное давление пара на наружной поверхности ограждения равным давлению пара в воздухе, соприкасающемся с данной поверхностью, т. е. рн. Из последней зависимости можно заключить, что падение парциального давления пара в однородном ограждении происходит по линейному закону (прямая линия в координатах р — δ). Кроме того, видно, что падение давления происходит интенсивнее при прохождении потока большей величины и в материалах, обладающих меньшим коэффициентом паропроницаемости. Знание температуры tx в слое х — х и парциального давления пара рх позволяет найти влажность воздуха и в этом слое φх = рх/ р”х и соответствующую равновесную влажность материала. Результаты расчета могут быть показаны на графиках t — δ и р — δ. Поскольку уравнение для tx позволяет определить температуру в каждом слое ограждения, то по этим значениям температур Влажность материала при относительной влажности воздуха могут быть найдены и соответствующие давления насыщенного водяного пара р”х в слоях ограждения. Так как изменение температуры по толщине однородного ограждения происходит по линейному закону, то изменение давления будет соответствовать логарифмическому закону связи между давлением и температурой насыщенного пара. При построении такой диаграммы могут встретиться два случая. Первый случай изображен на рис. 3.4, а для однородного ограждения и на рис. 3.4, б — для неоднородного. Его особенность заключается в том, что линия парциального давления рх проходит ниже линии р”х и нигде с нею не пересекается. Это значит, что водяной пар в ограждении нигде не становится насыщенным и, следовательно, конденсации влаги в ограждении не происходит. В данном случае увлажнение изоляции не угрожает. Линия φх= f (δх) протекает с наличием максимума там, где больше всего сближаются линии рх и р”х. Характерным является то, что максимум влажности воздуха и, следовательно, влажности (например, массовой — х) материала оказывается вблизи от холодной поверхности ограждения, но не у самой холодной поверхности.__
Такое же построение может быть выполнено и для неоднородного ограждения, состоящего из нескольких материалов с различным паропроницанием. В многослойном ограждении парциальное давление пара в различных слоях падает с неодинаковой скоростью, вследствие чего в плоскостях соприкосновения слоев различных материалов прямые рх — f (δх) получают переломы, образуя ломаную линию [см. и линию tx = f (δх)]. Особенностью второго случая оказывается пересечение линий рх и р”х (рис. 3.5, а), т. е. на некоторых участках ограждения пар, диффундирующий через ограждение, становится насыщенным, что вызывает его частичную конденсацию внутри ограждения. Часть толщины ограждения, где происходит конденсация пара, называется зоной конденсации.
Образование зоны конденсации (десублимации). Определение места расположения этой зоны в однородных и неоднородных ограждениях. Уравнения, описывающие эти процессы. Количества влаги, оседающее в зоне конденсации.
Часть толщины ограждения, где происходит конденсация пара, называется зоной конденсации. Было бы неверно считать зоной конденсации участок а — b между точками пересечения линий рх и р”х прежде всего потому, что отрезок ab прямой de теперь неправильно характеризует давление пара. Дело в том, что не существует пара, который бы имел давление выше, чем давление насыщенного пара того же вещества при той же температуре. Это значит, что в зоне конденсации пар должен иметь давление, равное давлению насыщенного пара, т. е. изменять свое состояние по линии acb. Линия dacbe не может быть графиком изменения давления пара в однородном ограждении, так как в точках а и b появились резкие изменения линий (переломы), что характерно только для неоднородных (многослойных) ограждений. Поскольку плавный переход от прямой линии к кривой может быть осуществлен только по касательной, то действительным графиком падения давления пара в ограждении может быть линия afcge, которая состоит из отрезков касательных df и ge, проведенных из точек d и е, к линии р”х = f (δх), и участка fcg самой линии р”х = f (δх) между точками касания fug. Последний участок ширины ограждения fcg и является действительной зоной конденсации. Графический метод нахождения зоны конденсации прости нагляден, но может быть недостаточно точным. Более точно зону конденсации можно установить аналитическим методом. Так, для определения координат точки g — правой границы зоны конденсации — необходимо решить уравнение (pg — рпм)/(δ— δх) = tg α или (pg — рпм)/(δ— δх) = dр”х/dδх при δх = δg. Для его решения надо найти р”х = f (δх), используя аналитические зависимости р”х = f1 (tx) и tx = f2 (δх), В качестве первой из них целесообразно привлечь довольно точную зависимость давления водяного пара надо льдом (мбар), данную Ф. Леви в виде lg р”х — 11,35 lg (tr + 140) — 23,9591 и справедливую в интервале от 0° до —40° С. Так как для однородной стенки tx = t'H — (δх/λ) q, то искомая функция lg р”х = 11,53 lg (t'H + 140 — (δх/λ) q) — 23,9591. (3.12) Решение уравнения (3.12) выполняется с помощью ЭВМ. Левая граница зоны конденсации - точка f — находится аналогично. Можно определить, какое количество влаги остается (конденсируется) в ограждении. Рисунок показывает, что наличие зоны конденсации изменило характер линии рх = f (δх) На участке касательной до зоны конденсации наклон ее больше наклона касательной после зоны конденсации. Из выражения (3.11а) следует, что в однородном ограждении разница в наклонах линии рх = f (δх) означает уменьшение потока влаги после зоны конденсации. Разница между потоками влаги до зоны конденсации и после нее определяет количество влаги (кг/с), которое конденсируется на 1 м2 поверхности ограждения. Можно обозначить это количество через Δw= w 1 — w 2, Тогда Δw= ((pн – pf))/Hdf) – ((pg — рпм)/Hge].__
|