Белгородский региональный институт повышения квалификации и профессиональной переподготовки специалистов
0.0181427 7.3. Пошук локального мінімуму аналітичної функції за допомогою вбудованих функцій системи Маthematica Система Mathematica надає вбудовану функцію пошуку локального мінімуму аналітичної функції. Вона має вигляд: FindMinimum [f (х), {х, x0}] де: f (х) - аналітична функція аргументу х; x0 - значення аргументу поблизу локального мінімуму. Функція FindMinimum [f (х), {х, x0}] знаходить координати всіх мінімумів функції f (х) шляхом її повторень стільки разів, скільки є локальних мінімумів. При цьому щоразу змінюється значення х0. Технологія відшукання мінімуму функції проста і полягає у виконанні наступних дій: 1. Побудова графіка аналітичної функції f (х) з метою визначення кількості екстремальних точок і вибору значень х0. 2. Введення вбудованою функції FindMinimum [f (х), {х, x0}] 3. Отримання рішення шляхом натискання комбінації клавіш <Shift> + <Еnter>. Якщо аналітична функція має максимум, то технологія залишається колишньою. Необхідно лише змінити знак функції f (х) на зворотний, помноживши її на -1. Розглянемо технологію визначення координат мінімуму аналітичної функції на прикладах. Приклад 7,7 Необхідно визначити координати екстремумів наступної аналітичної функції: x^4-13x^3 +35 x^2 +13 x-36. Процедури вирішення задачі наведено на рис. 7.7. З рис. 7.7 видно, що координатами точок мінімуму і максимуму є: [-0,17, -37], [2.63, 51.64], [7.29, -293.36]. Слід мати на увазі, що ординату максимуму необхідно помножити на -1. Цей метод порівняно з класичним має ту перевагу, що відгуком тут є координата мінімуму (х і y) і обчислення значень y не вимагається. Його недолік в тому, що він не дозволяє обчислити одночасно координати всіх екстремальних точок. f= х^4-13 х^3+35 х ^2+13 х -36 Рlot[f,{х,-2,10}] - 36+ 13х + 35х2 - 13 х3 + х4
FindMinimum[f,{x,-0.5}] {-37.1338, {х->-0.169441}} FindMinimum[-f,{x, 2}] {-51.6363, {х->2.63205}} FindMinimum[f,{x, 7}] {-293.358,{х->7.28739}} Крім функції FindMinimum [f (х), {х, x0}] система Mathematica має наступні чотири функції, що дозволяють відшукати локальний мінімум аналітичної функції: □ NMaximize [f, х] - шукає єдиний локальний максимум функції f (х); □ NMinimize [f, х] - шукає єдиний локальний мінімум функції f (х); □ NMaximize [{f, zху}, {х, у,... }] - шукає локальний максимум функції f (х), визначений умовою zху; □ NMinimize [{f, zху}, {х, у,...}] - шукає локальний мінімум функції f (х), визначений умовою zху. Технологія визначення локального максимуму (мінімуму) за допомогою приведених функцій практично не відрізняється від технології визначення локального мінімуму функцією FindMinimum [f (х), {х, х0}]. Наведемо приклади визначення екстремальних точок за допомогою цих функцій. Приклад 7,8 Необхідно знайти координати максимуму (мінімуму) аналітичних функцій: хе-x +1, 3х - 9x + 3. Спочатку побудуємо графік функції і визначимо, чи має функція екстремальні точку і яка вона (максимум або мінімум). По виду графіка виберемо вбудовану функцію. Рішення виконаємо в послідовності наведених функцій. Видно, що в результаті рішення отримані координати екстремальних точок, відповідні графіками. При цьому функції NMaximize [f, х] і NMinimize [f, х] не вимагають завдання аргументу поблизу локального максимуму (мінімуму), як це було у випадку використання функції FindMinimum [f (х), {х, x0}]. Розглянемо тепер випадок, коли аналітична функція має кілька екстремумів. Приклад 7,9 Необхідно визначити координати екстремальних точок наступних аналітичних функцій: ln (5-3х) + х2 -3, х5-5x4-4x3 +31 х2 + 2x-30. Рішення наведено на рис 7.9. Обговоримо результати вирішення завдань. При визначенні за допомогою функцій NMaximize [f, х], і NMinimize [f, х] координат екстремальних точок аналітичної функції, що має багато максимумів і мінімумів, виникає ряд проблем. У нашому прикладі функції мають кілька екстремальних точок: перша функція містить один максимум і один мінімум, друга - два максимуми і два мінімуми. Вирішуючи перше завдання, система визначила координати мінімуму і не знайшла координат максимуму (рішення абсурдно). У другій функції система знайшла тільки один максимум і один мінімум, що знаходяться зліва у графіка. Визначити координати інших екстремумів не вдається. У цьому істотний недолік функцій NMaximize [f, х] і NMinimize [f, х]. Існують функції NMinimize [{f, zху...}, {х, у,...}], NMinimize [{f, zху...}, {х, у,...}]. Ці функції знаходять координати екстремальних точок аналітичних функцій багатьох аргументів при обмеженнях zху.... f=х Ехр[-х]+1 Рlot[f,{х,0,5}] 1+ e-xх
NMaximize [f,х] {1.36788,{х->1.}} f1=З^х-9 х+3 Рlot[f1, {х,0,5}] 3+3Х- 9 х NMinimize [f1,х] {-6.03739, { х->1. 91439}}
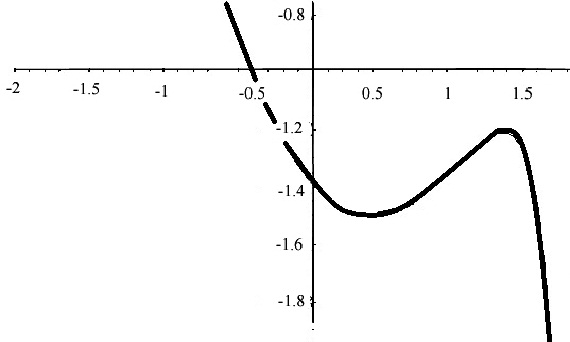
f2=Log[5-3x]+x^2-3 Plot[f2,{x,-2,3}] -3+x2+Log[5-3x]
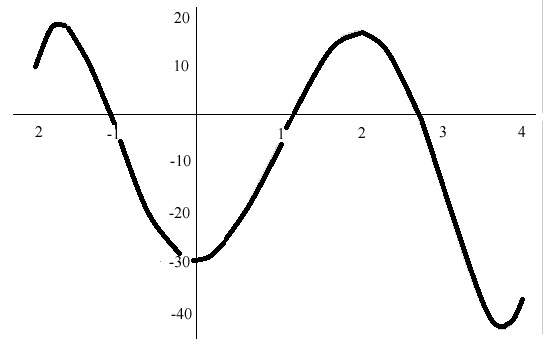
NMaximize[f2,х] {9. 65572578174896 × 10919, {х -> -9.82635526619558× 10459}} NMinimize [f2, х] {-1.50504,{х->0.392375}} fЗ=х^5-5 х^4-4 х^3+31 х^2+2 х-30 Рlot[f3,{х,-2,4}] -30 + 2 х + 31 х2 - 4 х3 - 5 х4 + х5
NMaximize[f3,х] {19.8942,{х->-1.68837}} NMinimize[f3,х] {-30.0321,{х->-0.0320697}} Наведемо приклади визначення координат функцій багатьох змінних, при обмеженнях на їх аргументи. Приклад 7,10 Необхідно визначити координати точок максимуму і мінімуму наступних функцій: sin x - ex+y, x+y <1; 2 х -4(х + у), х + у <5; 4(х + у +z) – 2x+y, х + у + z <7. У першої та другої функцій визначимо координати мінімуму, у третьої - максимуму. NMinimize[{Sin[х]-Exp[х+у],х+у<1},{x,у}] {-3.71828,{х→-1.5708,у→2.5708}} NMinimize[{2^x-4 (х+у),х+у<5},{х,у}] {-20., {х→-50.3938,у→55.3938}} NMaximize [ (4 (х+у+z)-2^ (х+у, х+у+z<7}, {х, у,z}] {28.,{x→1.13 548,у→-49.229, z→57.3645}}
7.4. Відшукання глобального максимуму (мінімуму) аналітичної функції Завдання пошуку глобального максимуму (мінімуму) є завданням математичного програмування. Серед цих завдань найбільш часто доводиться вирішувати завдання лінійного програмування. Завдання лінійного програмування формулюється таким чином. Задана наступна лінійна функція незалежних змінних x1, х2,..., xn: a1 x1 + a2 x2 +... + an xn, де a i - числа, звані коефіцієнтами лінійної функції, i = 1,2,..., п. Відомо також кілька рівнянь і нерівностей з незалежними змінними які є x1, х2,..., xn. Такими рівняннями (нерівностями) можуть бути: a1 x1 + a2 x2 +... + an xn = b (а1х1 + а2х2 +... + аn хn ≤ b), х i ≥ 0, i = 1,2,..., п і ряд інших. Серед безлічі варіантів, що задовольняють умовам обмеження, необхідно знайти сукупність змінних x1, х2,..., xn, при яких лінійна функція отримує максимальне (мінімальне) значення. Функція a1 x1 + a2 x2 +... + an xn в теорії математичного програмування називається цільовою функцією, а сукупність рівностей і нерівностей - обмеженнями. Сформульована задача лінійного програмування зустрічається на практиці дуже часто при вирішенні оптимізаційних завдань в техніці, управлінні, економіці. Система Мathematica має вбудовані функції вирішення завдань математичного програмування. Ці функції мають вигляд: СоnstrainedМах [f, {0}, {x1, х2,..., хn}] СоnstrainedMin [f, {0}, {x1, х2,..., хn}] LinearPrograming [с, m, b] У цих функціях прийняті наступні позначення: □ f - цільова функція; □ Q-вектор обмежень; □ X i -шукані незалежні змінні; □ з - мінімізована величина; □ m - обмеження; □ b - величина обмежень. Функція СоnstrainedМах [f, {0}, {x1, х2,..., хn}] шукає глобальний максимум, тобто такі значення хi, при яких виконуються всі обмеження Q, а цільова функція має максимальне значення. Функція СоnstrainedMin [f, {0}, {x1, х2,..., хn}] шукає глобальний мінімум, тобто такі значення хi, при яких виконуються всі обмеження о, а цільова функція має мінімальне значення. Функція LinearPrograming [с, m, b] шукає вектор х. с при умовах m. х> = b, х> = 0. Рішення такого складного завдання, як відшукання глобального максимуму (мінімуму), в системі Маthematica гранично просто: 1. Введення функції СоnstrainedМах [f, {0}, {x1, х2,..., хn}]. 2. Отримання рішення шляхом натискання комбінації клавіш <Shift> + <Enter>. Покажемо технологію відшукання глобального максимуму і мінімуму на конкретних прикладах. Приклад 7,11 Існує три технології випуску деякої продукції. Для її виготовлення необхідно мати три види сировини. Кожна з технологій вимагає певної кількості сировини даного виду, яке мається в обмеженій кількості. Обсяг виробленого продукту залежить від технології виготовлення і відомий для кожної з технологій. Необхідно знайти таку технологію, при якій обсяг випущеної продукції максимальний. Вихідні дані виробництва наведено в табл. 7.1.
Технологія виробництва допускає зміну способу виробництва протягом робочого дня. 7.4.1. Математичне формулювання задачі Позначимо x1, х2, х3 - частки робочого часу, що витрачається на виробництво заданого об'єму готового продукту за умови забезпечення сировиною, відповідно, за першої, другої і третьої технологіях. Обмеженнями при вирішенні цього завдання є: х1 ≥ 0, х2 ≥ 0, x3 ≥ 0; х1 + х2 + х3 ≤ 1; 2х1 + х2 +2 х3 ≤ 2; 3х1 + 2х2 + х3 ≤ 2; 2х1 + 3х2 + х3 ≤ 2. Обговоримо прийняті обмеження. Перше обмеження очевидне: долі робочого часу не можуть бути негативними. Друге припущення означає, що сумарний робочий час не повинен перевищувати повного робочого дня. Третє, четверте і п'яте допущення означають, що витрата сировини не повинна перевищувати ліміту (двійка для кожної сировини і технології). При будь-якій технології буде випущено продукту 30x1 +22 х2 +24 x3. Ця функція і є цільовою. У результаті рішення задачі потрібно визначити значення х1, х2, х3 і максимальне значення випущеного продукту, тобто визначити оптимальну технологію виробництва. У нашому випадку функція глобального максимуму буде мати вигляд: СоnstrainedMax [30 х1 +22 х2 +24 х3, {х1> = 0, х2> = 0, х3> = 0, 2 х1 + x2 + 2х3 <= 2, 3 х1 +2 х2 + хЗ, <= 2, 2 х1 + 3 х2 + х3, <= 2}, {х1, х2, х3}] Рішення завдання наведено на рис. 7.11. СоnstrainedMax[30*х1+22*х2+24*х3, { х1>=0, х2>=0, х3>=0, х1+х2+х3,<=1, 2 х1+ x2+ 2х3<=2, 3 х1+2 х2+хЗ<=2, 2 х1+3 х2+х3<=2}, {х1, х2, х3}] {27, {x1→ Видно, що підприємством за зміну буде випущено 27 одиниць продукції по першій і третій технологіям. Випуску продукції по другій технології не повинно бути. Класичною задачею лінійного програмування є транспортна задача. Наведемо і ми такий приклад. приклад 7,12 Є чотири складу товарів і три їх споживача. Відома також кількість товарів на кожному складі, потреби кожного споживача, а також вартість доставки товару до кожного споживача. Необхідно скласти оптимальний план перевезень, при якому сумарна вартість перевезень буде мінімальною. Вихідні дані задачі наведені в табл. 7.2.
Таблиця 7.2. Дані про перевезення товарів зі складів до споживачів
У таблиці позначено: □ С1, С2, С3, С4 - склади; □ П1, П2, П3 - споживачі; □ Zc - кількість товарів на складі; □ Zn-кількість товарів, необхідних споживачу. Цифри в таблиці означають вартість перевезень в умовних одиницях зі складу Сi, до споживача Пj, i = 1, 2, 3, 4, j = 1, 2, 3. У даному випадку цільовою буде наступна функція: 2n11 +4 n12 + n13 +4 n21 + n22 +2 n23 + 2n31 + 3n32 + 2n33 + n41 +2 n42 +3 n43, де nij - кількість товару, планованого для перевезення зі складу Ci, споживачеві Пj. Сформулюємо обмеження Q. Оскільки числа не можуть бути негативними, то n11 ≥ 0, n21 ≥ 0,..., n42 ≥ 0, n43 ≥ 0. Сумарна кількість продуктів на складах і потреби споживачів можна представити наступними рівняннями: n11 + n12 + n13 = 9; n21 + n22 + n23 = 7; n31 + n32 + n33 = 7; n41 + n42 + n43 = 7; n11 + n21 + n31 + n41 = 12; n12 + n22 + n32 + n42 = 10; n13 + n23 + n33 + n43 = 8. Сукупність нерівностей та цих рівнянь утворюють обмеження Q. Завдання полягає в тому, щоб знайти такі значення nij цільової функції, при яких сумарні витрати на перевезення були б мінімальними. Скористаємося функцією СоnstrainedMin [f, {0}, {x1, х2,..., хn}]. СоnstrainedMin [ 2*n11+4*n12+1*n13+4*n21+1*n22+2*n23+ 2*n31+3*n32+2*n33+1*n41+2*n42+3*n43, {n11>=0,n12>=0,n13>=0, n21>=0,n22>=0,n23>=0, n31>=0,n32>=0,n33>=о, n41>=0,n42>=0,n43>=0, n11+n12+n13==9,n21+n22+n23==7, n31+n32+n33==7, n41+n42+n43==7, n11+n21+n31+n41==12, n12+n22+n32+n42==10, n13+n23+n33+n43==8}, {n11,n12,n13,n21,n22,n23,n31,n32,n3 3, n41, n42,n43}] {41, {n11→1,n12→0,n13→8,n21→0,n22→7,n23→0 n31→4,n32→3,n33→0,n41→7,n42→0,n43→0} } Видно, що всі товари зі складів доставлені споживачам. Однак далеко не всі споживачі отримали товари з причини високої вартості перевезень. Белгородский региональный институт повышения квалификации и профессиональной переподготовки специалистов
Некоторые подходы к формированию системы оценки качества образования Выполнила: Цыбина Л.Н,
|




 , x2→0, x3→
, x2→0, x3→ 




