Нормализация.Мантисса в числах с ПЗ обычно представляется в нормализованной форме. Это означает, что на мантиссу налагаются такие условия, чтобы она по модулю была меньше единицы < 1), а первая цифра после точки отличалась от нуля. Полученная таким образом мантисса называется нормализованной. Для применяемых в ВМ систем счисления можно записать: · двоичная: · восьмеричная: · шестнадцатеричная: Если первые цифр мантиссы равны нулю, для нормализации ее нужно сдвинуть относительно запятой на i разрядов влево с одновременным уменьшением порядка на i единиц. В результате такой операции число не изменяется.
В примере для шестнадцатеричной системы после нормализации старшая цифра в двоичном представлении содержит впереди три нуля (0001). Это несколько уменьшает точность представления чисел по сравнению с двоичной системой при одинаковом числе двоичных разрядов, отведенных под мантиссу. Если для записи числа с ПЗ используется база 2 (q = 2), то часто применяют еще один способ повышения точности представления мантиссы, называемый приемом скрытой единицы. Суть его в том, что в нормализованной мантиссе старшая цифра всегда равна единице (для представления нуля используется специальная кодовая комбинация), следовательно, эта цифра может не записываться, а подразумеваться. Запись мантиссы начинают с ее второй цифры, и это позволяет задействовать дополнительный значащий бит для более точного представления числа. Следует отметить, что значение порядка в данном случае не меняется. Скрытая единица перед выполнением арифметических операций восстанавливается, а при записи результата — удаляется. Таким образом, нормализованная мантисса 0,101000(1) при использовании способа «скрытой единицы» будет иметь вид 0,010001 (в скобках указана цифра, не поместившаяся в поле мантиссы при стандартной записи). Для более существенного увеличения точности вычислений под число отводят несколько машинных слов, например два. Дополнительные биты, как правило, лужат для увеличения разрядности мантиссы, однако в ряде случаев часть из них может отводиться и для расширения поля порядка. В процессе вычислений может получаться ненормализованное число. В таком случае ВМ, если это предписано командой, автоматически нормализует его.
Сдвиг В дополнение к побитовым логическим операциям, практически во всех АСК предусмотрены команды для реализации операций логического, арифметического и циклического сдвигов (рис. 2.32).
Рис. 2.32. Варианты операций сдвига
При логическом сдвиге влево или вправо (см. рис. 2.32, а), сдвигаются все разряды слова. Биты, вышедшие за пределы разрядной сетки, теряются, а освободившиеся позиции заполняются нулями. При арифметическом сдвиге (см. рис. данные трактуются как целые числа со знаком, причем бит знака не изменяет положения. При сдвиге вправо освободившиеся позиции заполняются значением знакового разряда, а при сдвиге влево - нулями. Арифметические сдвиги позволяют ускорить выполнение некоторых арифметических операций. Так, если числа представлены двоичным дополнительным кодом, то сдвиги влево и вправо эквивалентны соответственно умножению и делению на 2. При циклическом сдвиге (см. рис. 2.32, в) смещаются все разряды слова, причем значение разряда, выходящего за пределы слова, заносится в позицию, освободившуюся с противоположной стороны, то есть потери информации не происходит. Одно из возможных применений циклических сдвигов - это перемещение интересующего бита в крайнюю левую (знаковую) позицию, где он может быть проанализирован как знак числа. 9. Упакованные данные. SIMD – команды. В последних версиях АСК, предусматривающих особые команды обработки мультимедийной информации, помимо упакованных целых чисел используются и упакованные числа с плавающей запятой. Так, в уже упоминавшейся технологии 3DNow! фирмы AMD имеются команды, служащие для увеличения производительности систем при обработке трехмерных приложений, описываемых числами с ПЗ. Каждая такая команда работает с двумя операндами с плавающей запятой одинарной точности. Операнды упаковываются в 64-разрядные группы, как это показано на рис. 2.25.
Рис. 2.25. Формат упакованных чисел с плавающей запятой в технологиях 3DNow!, SSE, SSE2 В микропроцессорах фирмы Intel, начиная с Pentium III, для аналогичных целей поддержаны команды, реализующие технологию SSE, также ориентированную на параллельную обработку упакованных чисел с ПЗ. Здесь числа объединяются в группы длиной 128 бит, и это позволяет упаковать в группу четыре 32-разрядных числа с ПЗ (числа с одинарной точностью). Позже, в технологии SSE2, которую можно считать дальнейшим развитием SSE, появился формат, где в группу из 128 бит упаковываются два 64-разрядных числа с ПЗ, то есть числа, представленные с двойной точностью. SIMD – команды Название данного типа команд представляет собой аббревиатуру от Single Instruction Multiple Data — буквально «одна инструкция — много данных». В отличие от обычных команд, оперирующих двумя числами, SIMD-команды обрабатывают сразу две группы чисел (в принципе их можно называть групповыми командами). Операнды таких команд обычно представлены в одном из упакованных форматов. Идея была выдвинута в Институте точной механики и вычислительной техники им. С. А. Лебедева в 1978 году в рамках проекта С 1992 года команды типа SIMD становятся неотъемлемым элементом АСК микропроцессоров фирм Intel и AMD. Поводом послужило широкое распространение мультимедийных приложений. Видео, трехмерная графика и звук в ВМ представляются большими массивами данных, элементы которых чаще всего обрабатываются идентично. Так, при сжатии видео и преобразовании его в формат MPEG один и тот же алгоритм применяется к тысячам битов данных. В трехмерной графике часто встречаются операции, которые можно выполнить за один такт: интерполирование и нормировка векторов, вычисление скалярного произведения векторов, интерполяция компонентов цвета и т. д. Включение SIMD-команд в АСК позволяет существенно ускорить подобные вычисления. Первой на мультимедийный бум отреагировала фирма Intel, добавив в систему команд своего микропроцессора Pentium 57 SIMD-команд. Название ММХ (MultiMedia eXtention - мультимедийное расширение) разработчики обосновывали тем, что при выборе состава новых команд были проанализированы алгоритмы, применяемые в различных мультимедийных приложениях. Команды ММХ обеспечивали параллельную обработку упакованных целых чисел. При выполнении арифметических операций каждое из чисел, входящих в группу, рассматривается как самостоятельное, без связи с соседними числами. Учитывая специфику обрабатываемой информации, команды ММХ реализуют так называемую арифметику с насыщением: если в результате сложения образуется число, выходящее за пределы отведенных под него позиций, оно заменяется наибольшим двоичным числом, которое в эти позиции вмещается. На рис. 2.33 показано сложение двух групп четырехразрядных целых чисел, упакованных в 32-разрядные слова.
Следующим шагом стало создание новых наборов работающих также с операндами, представленными в виде упакованных чисел с плавающей запятой. Такие команды в соответствующих приложениях повышают производительность процессора примерно вдвое. Первой подобную технологию в середине 1998 года предложила фирма AMD в микропроцессоре К6-2. Это мультимедийное расширение включало в себя 21 и получило название 3DNow!. Расширение 3DNow! в дополнение к целочисленной информации типа ММХ позволяло оперировать парой упакованных чисел в формате с плавающей запятой. Полугодом позже фирма Intel ввела в свои микропроцессоры так называемые потоковые обозначив их аббревиатурой SSE - Streaming SIMD Extension (потоковая обработка по принципу «одна команда - много данных»). Сначала это были 70 команд в микропроцессоре Pentium III. Команды дополняли групповые целочисленные операции ММХ и расширяли счет групповых опе раций с 32-разрядными вещественными числами. В зависимости от типа чисел (целые или вещественные) команды SSE делятся на три категории: • работа с упакованными группами целых чисел, которые могут иметь размер байта, слова, двойного слова или квадрослова (количество чисел в группе зависит от их разрядности и от разрядности всей группы — 64 или 128); • оперирование одной парой 32-разрядных или 64-разрядных чисел с плавающей запятой (обычная или двойная точность); • обработка четырех пар вещественных чисел обычной точности или двух пар вещественных чисел двойной точности. Дальнейшее развитие технологии SSE вылилось в SSE2 и получило реализацию в Pentium 4. Этот вариант включает в себя 271 команду и позволяет выполнять групповые арифметические и логические операции, сдвиги, сравнения чисел, перегруппировку и извлечение отдельных чисел, различные варианты пересылок. За один такт обрабатываются четыре 32-разрядных числа с плавающей запятой, упакованных в 128-разрядное слово. Новый импульс получила и технология 3DNow!, более совершенный вариант которой получил название Enhanced 3DNow!. Этот набор команд близок к SSE2.
|
(1 >|q\- S);
(1 > |q\ =?);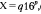
(1 >\q\ = 1/16).
