Преподаватель: Валентинов В.А.
Специальность: 080100.62 - Экономика
Группа: 1
Дисциплина: Эконометрика
Логин:05ps1391772
Начало тестирования: 2013-02-18 00:32:13
Завершение тестирования: 2013-02-18 00:32:18
Продолжительность тестирования: 0 мин.
Заданий в тесте: 31
Кол-во правильно выполненных заданий: 0
Процент правильно выполненных заданий: 0 %
 ЗАДАНИЕ N 1 отправить сообщение разработчикам
ЗАДАНИЕ N 1 отправить сообщение разработчикам
Тема: Спецификация эконометрической модели
Ошибки спецификации эконометрической модели имеют место вследствие …

|
| | неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора
|
|
|
| | недостоверности или недостаточности исходной информации
|
|
|
| | неоднородности данных в исходной статистической совокупности
|
|
|
| | недостаточного количества данных
|
Решение:
Спецификацией модели называется отбор факторов, включаемых в модель, и выбор математической функции для  . Поэтому к ошибкам спецификации относятся не только неправильный выбор той или иной математической функции для
. Поэтому к ошибкам спецификации относятся не только неправильный выбор той или иной математической функции для  , но и недоучет в уравнении регрессии какого-то существенного фактора, то есть использование парной регрессии вместо множественной.
, но и недоучет в уравнении регрессии какого-то существенного фактора, то есть использование парной регрессии вместо множественной.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 45.
Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2 т. 2-е изд., испр. – Т. 2: Айвазян С.А. Основы эконометрики. – М.: ЮНИТИ-ДАНА, 2001. – С. 20–30.
 ЗАДАНИЕ N 2 отправить сообщение разработчикам
ЗАДАНИЕ N 2 отправить сообщение разработчикам
Тема: Отбор факторов, включаемых в модель множественной регрессии
Дана матрица парных коэффициентов корреляции.

Коллинеарными являются факторы …
Решение:
Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если  . В нашей модели только коэффициент парной линейной регрессии между факторами
. В нашей модели только коэффициент парной линейной регрессии между факторами  и
и  больше 0,7.
больше 0,7.  , значит, факторы
, значит, факторы  и
и  коллинеарны.
коллинеарны.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 113.
Магнус, Ян Р. Эконометрика: нач. курс: [учеб. для студентов вузов по экон. специальностям] / Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий; Акад. нар. хоз-ва при Правительстве РФ. – М.: Дело, 2005. – С. 98–100.
 ЗАДАНИЕ N 3 отправить сообщение разработчикам
ЗАДАНИЕ N 3 отправить сообщение разработчикам
Тема: Фиктивные переменные
При исследовании зависимости потребления мяса от уровня дохода и пола потребителя можно рекомендовать …

|
| | использовать фиктивную переменную – пол потребителя
|

|
| | разделить совокупность на две: для потребителей женского пола и для потребителей мужского пола
|
|
|
| | использовать фиктивную переменную – уровень дохода
|
|
|
| | исключить из рассмотрения пол потребителя, так как данный фактор нельзя измерить количественным образом
|
Решение:
При построении регрессионной модели может возникнуть ситуация, когда необходимо включить в уравнение помимо количественных переменных переменные, отражающие некоторые атрибутивные признаки (пол, образование, регион и т.п.). Такого рода качественные переменные называются «фиктивными» (dummy) переменными. Они отражают неоднородность исследуемой статистической совокупности и используются для более качественного моделирования зависимостей в таких неоднородных объектах наблюдения. При моделировании отдельных зависимостей по неоднородным данным можно также воспользоваться способом разделения всей совокупности неоднородных данных на несколько отдельных совокупностей, количество которых равно количеству состояний dummy-переменной. Таким образом правильными вариантами ответов являются: «использовать фиктивную переменную – пол потребителя» и «разделить совокупность на две: для потребителей женского пола и для потребителей мужского пола».
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 121–127.
 ЗАДАНИЕ N 4 отправить сообщение разработчикам
ЗАДАНИЕ N 4 отправить сообщение разработчикам
Тема: Линейное уравнение множественной регрессии
Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …
Решение:
Коэффициент детерминации  равен доле дисперсии, объясненной регрессией, в общей дисперсии. Величина (
равен доле дисперсии, объясненной регрессией, в общей дисперсии. Величина ( ) показывает долю остаточной дисперсии в общей или дисперсию, вызванную влиянием остальных, не учтенных в модели факторов.
) показывает долю остаточной дисперсии в общей или дисперсию, вызванную влиянием остальных, не учтенных в модели факторов.
 . Значит,
. Значит, 
Магнус, Ян Р. Эконометрика: нач. курс: [учеб. для студентов вузов по экон. специальностям] / Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий; Акад. нар. хоз-ва при Правительстве РФ. – М.: Дело, 2005. С.46–50.
 ЗАДАНИЕ N 5 отправить сообщение разработчикам
ЗАДАНИЕ N 5 отправить сообщение разработчикам
Тема: Оценка параметров линейных уравнений регрессии
В эконометрической модели уравнения регрессии величина отклонения фактического значения зависимой переменной от ее расчетного значения характеризует …

|
| | ошибку модели
|
|
|
| | величину коэффициента регрессии
|
|
|
| | значение свободного члена уравнения
|
|
|
| | нулевое значение независимой переменной
|
Решение:
Одним из типов эконометрических моделей является уравнение регрессии, которое может быть записано в виде математического выражения  , где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); f – тип функциональной зависимости (математическая функция);
, где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); f – тип функциональной зависимости (математическая функция); 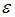 – случайные факторы. При этом
– случайные факторы. При этом  , тогда
, тогда  , где
, где  – фактическое значение зависимой переменной,
– фактическое значение зависимой переменной,  – расчетное значение зависимой переменной,
– расчетное значение зависимой переменной,  – ошибка модели. Поэтому правильный ответ – «ошибку модели».
– ошибка модели. Поэтому правильный ответ – «ошибку модели».
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 7–10.
 ЗАДАНИЕ N 6 отправить сообщение разработчикам
ЗАДАНИЕ N 6 отправить сообщение разработчикам
Тема: Предпосылки МНК, методы их проверки
Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле  , где
, где  – значение коэффициента автокорреляции остатков модели. Минимальная величина значения
– значение коэффициента автокорреляции остатков модели. Минимальная величина значения  будет наблюдаться при ________ автокорреляции остатков.
будет наблюдаться при ________ автокорреляции остатков.

|
| | положительной
|
|
|
| | отрицательной
|
|
|
| | нулевой
|
|
|
| | бесконечно малой
|
Решение:
Значение коэффициента автокорреляции остатков модели  рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если
рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если  , то
, то  ; если
; если  , то
, то  . Поэтому значение
. Поэтому значение  меняется от 0 до 4. Минимальное значение
меняется от 0 до 4. Минимальное значение  равно 0 для случая, когда
равно 0 для случая, когда  , то есть для положительной автокорреляции остатков.
, то есть для положительной автокорреляции остатков.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 436 – 442.
Бывшев, В.А. Эконометрика: учеб. пособие / В.А. Бывшев. – М.: Финансы и статистика, 2008 – С 189 – 194.
 ЗАДАНИЕ N 7 отправить сообщение разработчикам
ЗАДАНИЕ N 7 отправить сообщение разработчикам
Тема: Свойства оценок параметров эконометрической модели, получаемых при помощи МНК
Из несмещенности оценки параметра следует, что среднее значение остатков равно …

|
| |
|
|
|
| |
|
|
|
| | -1
|
|
|
| | 
|
Решение:
Желательными свойствами оценок параметров регрессионной модели являются состоятельность, несмещенность и эффективность. Понятие несмещенности оценки формулируется следующим образом: «Оценка 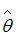 параметра
параметра  называется несмещенной, если математическое ожидание
называется несмещенной, если математическое ожидание  »; где
»; где  – истинное значение параметра, вычисленное для генеральной совокупности. Математическое ожидание
– истинное значение параметра, вычисленное для генеральной совокупности. Математическое ожидание  в том случае, если
в том случае, если  .
.
Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2 т. 2-е изд., испр. – Т. 2: Айвазян С.А. Основы эконометрики. – М.: ЮНИТИ-ДАНА, 2001. – С. 63.
Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 77–82.
 ЗАДАНИЕ N 8 отправить сообщение разработчикам
ЗАДАНИЕ N 8 отправить сообщение разработчикам
Тема: Обобщенный метод наименьших квадратов (ОМНК)
Пусть y – издержки производства,  – объем продукции,
– объем продукции,  – основные производственные фонды,
– основные производственные фонды,  – численность работников. Известно, что в уравнении
– численность работников. Известно, что в уравнении  дисперсии остатков пропорциональны квадрату объема продукции
дисперсии остатков пропорциональны квадрату объема продукции  .
.
Применим обобщенный метод наименьших квадратов, поделив обе части уравнения на  После применения обобщенного метода наименьших квадратов новая модель приняла вид
После применения обобщенного метода наименьших квадратов новая модель приняла вид  . Тогда параметр
. Тогда параметр  в новом уравнении характеризует среднее изменение затрат на единицу продукции при увеличении …
в новом уравнении характеризует среднее изменение затрат на единицу продукции при увеличении …

|
| | фондоемкости продукции при неизменном уровне трудоемкости продукции
|
|
|
| | трудоемкости продукции при неизменном уровне фондоемкости продукции
|
|
|
| | производительности труда при неизменном уровне фондовооруженности труда
|
|
|
| | фондовооруженности труда при неизменном уровне производительности труда
|
Решение:
Пусть y – издержки производства,  – объем продукции,
– объем продукции,  – основные производственные фонды,
– основные производственные фонды,  – численность работников. Известно, что в уравнении
– численность работников. Известно, что в уравнении  дисперсии остатков пропорциональны квадрату объема продукции
дисперсии остатков пропорциональны квадрату объема продукции  .
.
После применения обобщенного метода наименьших квадратов новая модель приняла вид  . Новая модель имеет дело с новыми переменными
. Новая модель имеет дело с новыми переменными  – затраты на единицу продукции,
– затраты на единицу продукции,  – фондоемкость продукции,
– фондоемкость продукции,  – трудоемкость продукции. В новой модели параметр
– трудоемкость продукции. В новой модели параметр  показывает среднее изменение затрат на единицу продукции
показывает среднее изменение затрат на единицу продукции  с увеличением на единицу фондоемкости продукции
с увеличением на единицу фондоемкости продукции  при неизменном уровне трудоемкости продукции
при неизменном уровне трудоемкости продукции  .
.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 206.
 ЗАДАНИЕ N 9 отправить сообщение разработчикам
ЗАДАНИЕ N 9 отправить сообщение разработчикам
Тема: Оценка тесноты связи
Для регрессионной модели вида 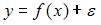 получена диаграмма
получена диаграмма

Такое графическое отображение называется …

|
| | полем корреляции
|
|
|
| | диаграммой детерминации
|
|
|
| | полем детерминации
|
|
|
| | коррелограммой
|
Решение:
Графическое отображение совокупности точек с координатами  на плоскости для зависимости
на плоскости для зависимости  от
от  называется полем корреляции, или диаграммой рассеяния. Поэтому верный ответ – «полем корреляции».
называется полем корреляции, или диаграммой рассеяния. Поэтому верный ответ – «полем корреляции».
 ЗАДАНИЕ N 10 отправить сообщение разработчикам
ЗАДАНИЕ N 10 отправить сообщение разработчикам
Тема: Оценка качества подбора уравнения
Если общая сумма квадратов отклонений  , и остаточная сумма квадратов отклонений
, и остаточная сумма квадратов отклонений  , то сумма квадратов отклонений, объясненная регрессией, равна …
, то сумма квадратов отклонений, объясненная регрессией, равна …

|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| | 0,25
|
Решение:
Общая сумма квадратов отклонений складывается из суммы квадратов отклонений, объясненных регрессией, и остаточной сумма квадратов отклонений.

Значит, сумма квадратов отклонений, объясненная регрессией, равна разности общей сумме квадратов отклонений и остаточной суммы квадратов отклонений.
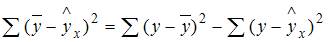
Получается  .
.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 137.
 ЗАДАНИЕ N 11 отправить сообщение разработчикам
ЗАДАНИЕ N 11 отправить сообщение разработчикам
Тема: Проверка статистической значимости эконометрической модели
При расчете скорректированного коэффициента множественной детерминации пользуются формулой  , где …
, где …

|
| | n – число наблюдений; m – число факторов, включенных в модель множественной регрессии
|
|
|
| | m – число наблюдений; n – число факторов, включенных в модель множественной регрессии
|
|
|
| | n – число параметров при независимых переменных; m – число факторов, включенных в модель множественной регрессии
|
|
|
| | n – число параметров при независимых переменных; m – число наблюдений
|
Решение:
Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и имеет вид  , где n – число наблюдений, m – число факторов, включенных в модель множественной регрессии.
, где n – число наблюдений, m – число факторов, включенных в модель множественной регрессии.
Магнус, Ян Р. Эконометрика: нач. курс: [учеб. для студентов вузов по экон. специальностям] / Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий; Акад. нар. хоз-ва при Правительстве РФ. – М.: Дело, 2005. C. 67–70.
 ЗАДАНИЕ N 12 отправить сообщение разработчикам
ЗАДАНИЕ N 12 отправить сообщение разработчикам
Тема: Оценка значимости параметров эконометрической модели
Для уравнения множественной регрессии вида  на основании 14 наблюдений рассчитаны оценки параметров и записана модель:
на основании 14 наблюдений рассчитаны оценки параметров и записана модель:  (в скобках указаны значения t -статистики соответствующие параметрам регрессии). Известны критические значения Стьюдента для различных уровней значимости
(в скобках указаны значения t -статистики соответствующие параметрам регрессии). Известны критические значения Стьюдента для различных уровней значимости



Для данного уравнения при уровне значимости α=0,05 значимыми являются параметры …
Решение:
Чтобы оценить значимость параметров регрессии используется t -критерий Стьюдента. Для каждого коэффициента регрессии  формулируется нулевая гипотеза
формулируется нулевая гипотеза  при альтернативной гипотезе
при альтернативной гипотезе  . Затем рассчитывается фактическое значение t -статистики, которое сравнивается с критическим значением Стьюдента
. Затем рассчитывается фактическое значение t -статистики, которое сравнивается с критическим значением Стьюдента  для требуемого числа степеней свободы и уровня значимости. Если
для требуемого числа степеней свободы и уровня значимости. Если  , коэффициент
, коэффициент  значим; если
значим; если  коэффициент
коэффициент  незначим. В нашем случае при уровне значимости 0,05 значимыми является параметры
незначим. В нашем случае при уровне значимости 0,05 значимыми является параметры 
Эконометрика. Под ред. Елисеевой И.И., М.: Финансы и статистика, 2005. С.160–165.
Кремер, Н.Ш. Эконометрика: учеб. для студентов вузов / Н. Ш. Кремер, Б. А. Путко; ред. Н. Ш. Кремер. – М.: ЮНИТИ, 2002. – С.40–52.
 ЗАДАНИЕ N 13 отправить сообщение разработчикам
ЗАДАНИЕ N 13 отправить сообщение разработчикам
Тема: Нелинейные зависимости в экономике
Если с увеличением масштабов производства удельный расход сырья сокращается, то моделирование целесообразно проводить на основе …

|
| | равносторонней гиперболы
|
|
|
| | степенной функции
|
|
|
| | параболы второй степени
|
|
|
| | показательной функции
|
Решение:
Равносторонняя гипербола обычно используется в эконометрике для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции, поскольку она позволяет учесть эффект масштаба, что с увеличением объемов выпускаемой продукции удельные показатели расходов сырья, материалов или топлива обычно падают.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 82.
Бывшев В.А. Эконометрика: учеб. пособие / В.А. Бывшев. – М.: Финансы и статистика, 2008. – С.331–346.
 ЗАДАНИЕ N 14 отправить сообщение разработчикам
ЗАДАНИЕ N 14 отправить сообщение разработчикам
Тема: Виды нелинейных уравнений регрессии
Гиперболической моделью не является регрессионная модель …
Решение:
Одним из видов нелинейных зависимостей в эконометрике являются гиперболические зависимости в виде функции, в которых независимая переменная находится в знаменателе дроби в степени (–1), (–2) и т.д. Как правило, в таких моделях параметры являются линейными. Рассмотрим уравнения:

 которые представляют одну и ту же модель, так как
которые представляют одну и ту же модель, так как  и оба уравнения они отражают гиперболическую зависимость y от x.
и оба уравнения они отражают гиперболическую зависимость y от x.
В уравнении  независимая переменная x представлена в степени (–1) и (–2), и это тоже гиперболическая модель.
независимая переменная x представлена в степени (–1) и (–2), и это тоже гиперболическая модель.
А в уравнении  переменная х представлена в степени 1, и это линейное уравнение регрессии с коэффициентом регрессии
переменная х представлена в степени 1, и это линейное уравнение регрессии с коэффициентом регрессии  . Поэтому уравнение
. Поэтому уравнение  не является гиперболической моделью.
не является гиперболической моделью.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 77.
 ЗАДАНИЕ N 15 отправить сообщение разработчикам
ЗАДАНИЕ N 15 отправить сообщение разработчикам
Тема: Линеаризация нелинейных моделей регрессии
Для линеаризации нелинейной функции  может быть применен метод …
может быть применен метод …

|
| | логарифмирования и замены переменных
|
|
|
| | разложения функции в ряд Тейлора
|
|
|
| | потенцирования и замены переменных
|
|
|
| | обращения и замены переменных
|
Решение:
Функция  является внутренне линейной и с помощью логарифмирования может быть преобразована к виду
является внутренне линейной и с помощью логарифмирования может быть преобразована к виду  , которая является линейной относительно логарифмов переменных. Сделав замену переменных
, которая является линейной относительно логарифмов переменных. Сделав замену переменных  ,
,  ,
,  ,
,  , получим линейную функцию
, получим линейную функцию  . Поэтому для линеаризации используется сначала логарифмирование, затем замена переменных.
. Поэтому для линеаризации используется сначала логарифмирование, затем замена переменных.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 96–99.
Бывшев В.А. Эконометрика: учеб. пособие / В.А. Бывшев. – М.: Финансы и статистика, 2008. – С.331–346.
 ЗАДАНИЕ N 16 отправить сообщение разработчикам
ЗАДАНИЕ N 16 отправить сообщение разработчикам
Тема: Оценка качества нелинейных уравнений регрессии
По 20 регионам страны изучалась зависимость уровня безработицы y (%) от индекса потребительских цен x (% к предыдущему году) и построено уравнение в логарифмах исходных показателей:  . Коэффициент корреляции между логарифмами исходных показателей составил
. Коэффициент корреляции между логарифмами исходных показателей составил  . Коэффициент детерминации для модели в исходных показателях равен …
. Коэффициент детерминации для модели в исходных показателях равен …
Решение:
Коэффициент детерминации для модели в исходных показателях в данном случае будет равен коэффициенту детерминации для модели в логарифмах исходных показателей, который вычисляется как квадрат коэффициента корреляции, то есть 0,64.
Бывшев В.А. Эконометрика: учеб. пособие / В.А. Бывшев. – М.: Финансы и статистика, 2008. – С.331–346.
 ЗАДАНИЕ N 17 отправить сообщение разработчикам
ЗАДАНИЕ N 17 отправить сообщение разработчикам
Тема: Временные ряды данных: характеристики и общие понятия
Совокупность значений экономического показателя за несколько последовательных моментов (периодов) времени называется …

|
| | временным рядом
|
|
|
| | тенденцией
|
|
|
| | коррелограммой
|
|
|
| | автокорреляционной функцией
|
Решение:
Совокупность значений экономического показателя за несколько последовательных моментов (периодов) времени называется временным рядом.
Эконометрика: учеб. / И.И. Елисеева [и др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 296.
 ЗАДАНИЕ N 18 отправить сообщение разработчикам
ЗАДАНИЕ N 18 отправить сообщение разработчикам
Тема: Структура временного ряда
Автокорреляцией уровней ряда называется корреляционная зависимость между …

|
| | последовательными уровнями ряда
|
|
|
| | уровнями двух рядов
|
|
|
| | компонентами, образующими уровни ряда
|
|
|
| | факторами, формирующими уровень ряда
|
Решение:
Автокорреляцией уровней ряда называется корреляционная зависимость между последовательными уровнями ряда.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 298.
 ЗАДАНИЕ N 19 отправить сообщение разработчикам
ЗАДАНИЕ N 19 отправить сообщение разработчикам
Тема: Аддитивная и мультипликативная модели временных рядов
Для аддитивной модели временного ряда Y = T + S + E лаг модели равен 4 и известны значения трех скорректированных сезонных компонент:  ,
,  ,
,  .
.  равна …
равна …
Решение:
Для аддитивной модели временного ряда Y = T + S + E сумма скорректированных сезонных компонент равна нулю.  .
.
Значит, 
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 312–316.
 ЗАДАНИЕ N 20 отправить сообщение разработчикам
ЗАДАНИЕ N 20 отправить сообщение разработчикам
Тема: Модели стационарных и нестационарных временных рядов и их идентификация
Для временного ряда известны характеристики: 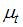 – среднее и
– среднее и  – дисперсия. Если временной ряд является стационарным, то …
– дисперсия. Если временной ряд является стационарным, то …
Решение:
При моделировании временных рядов рассматривается отдельный класс – стационарные временные ряды. Основные характеристики стационарного временного ряда состоят в том, что среднее 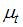 и дисперсия стохастического процесса, сгенерировавшего конкретный временной, не зависят от времени t, то есть
и дисперсия стохастического процесса, сгенерировавшего конкретный временной, не зависят от времени t, то есть  ;
;  .
.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 335 – 336.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 284–288.
 ЗАДАНИЕ N 21 отправить сообщение разработчикам
ЗАДАНИЕ N 21 отправить сообщение разработчикам
Тема: Общие понятия о системах уравнений, используемых в эконометрике
Модель равенства спроса и предложения, где предложение  и спрос
и спрос  являются линейными функциями цены p, состоит из уравнений …
являются линейными функциями цены p, состоит из уравнений …
Решение:
В модели предложение  и спрос
и спрос  являются линейными функциями цены p. Значит, уравнение для предложения
являются линейными функциями цены p. Значит, уравнение для предложения  будет иметь вид
будет иметь вид  , а уравнение для спроса
, а уравнение для спроса  –
–  . Так как рассматривается модель равенства спроса и предложения, значит, первые два уравнения должны быть дополнены третьим:
. Так как рассматривается модель равенства спроса и предложения, значит, первые два уравнения должны быть дополнены третьим:  .
.
Модель будет иметь вид
 ,
,
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С.341–355.
 ЗАДАНИЕ N 22 отправить сообщение разработчикам
ЗАДАНИЕ N 22 отправить сообщение разработчикам
Тема: Классификация систем уравнений
Установите соответствие между классом и видом системы эконометрических уравнений:
(1) система одновременных уравнений
(2) система рекурсивных уравнений
(3) система независимых уравнений
Решение:
Рассмотрим каждую из систем эконометрических уравнений.
(3) – система независимых уравнений. В такой системе в правой части уравнений стоят только независимые переменные, которые не могут находиться в левой части других уравнений системы. Поэтому для системы (3) правильным вариантом ответа является система

(1) – система одновременных (взаимозависимых) уравнений. В правой части уравнений такой системы одновременно с независимыми переменными стоят и зависимые переменные, которые в других уравнениях находятся в левой части и являются функциями набора зависимых и/или независимых переменных. Порядок следования зависимых переменных y в правой части уравнений не зависит от количества предыдущих уравнений. Поэтому для системы (1) правильным вариантом ответа является система 
(2) является системой рекурсивных уравнений. В такой системе в правой части уравнений стоят как зависимые, так и независимые переменные; при этом каждое последующее уравнение в правой части включает зависимые переменные y только предыдущих уравнений системы. Поэтому для системы (2) правильным вариантом ответа является система 
Система  содержит ошибку, так как в левой час
содержит ошибку, так как в левой час

 ЗАДАНИЕ N 1 отправить сообщение разработчикам
ЗАДАНИЕ N 1 отправить сообщение разработчикам
 . Поэтому к ошибкам спецификации относятся не только неправильный выбор той или иной математической функции для
. Поэтому к ошибкам спецификации относятся не только неправильный выбор той или иной математической функции для 
 и
и 

 . В нашей модели только коэффициент парной линейной регрессии между факторами
. В нашей модели только коэффициент парной линейной регрессии между факторами  , значит, факторы
, значит, факторы 

 равен доле дисперсии, объясненной регрессией, в общей дисперсии. Величина (
равен доле дисперсии, объясненной регрессией, в общей дисперсии. Величина ( ) показывает долю остаточной дисперсии в общей или дисперсию, вызванную влиянием остальных, не учтенных в модели факторов.
) показывает долю остаточной дисперсии в общей или дисперсию, вызванную влиянием остальных, не учтенных в модели факторов.  . Значит,
. Значит, 
 , где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); f – тип функциональной зависимости (математическая функция);
, где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); f – тип функциональной зависимости (математическая функция); 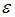 – случайные факторы. При этом
– случайные факторы. При этом  , тогда
, тогда  , где
, где  – фактическое значение зависимой переменной,
– фактическое значение зависимой переменной,  – расчетное значение зависимой переменной,
– расчетное значение зависимой переменной,  – ошибка модели. Поэтому правильный ответ – «ошибку модели».
– ошибка модели. Поэтому правильный ответ – «ошибку модели». , где
, где  – значение коэффициента автокорреляции остатков модели. Минимальная величина значения
– значение коэффициента автокорреляции остатков модели. Минимальная величина значения  будет наблюдаться при ________ автокорреляции остатков.
будет наблюдаться при ________ автокорреляции остатков. рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если
рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если  , то
, то  ; если
; если  , то
, то  . Поэтому значение
. Поэтому значение  равно 0 для случая, когда
равно 0 для случая, когда  , то есть для положительной автокорреляции остатков.
, то есть для положительной автокорреляции остатков.
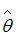 параметра
параметра  называется несмещенной, если математическое ожидание
называется несмещенной, если математическое ожидание  »; где
»; где  .
. – численность работников. Известно, что в уравнении
– численность работников. Известно, что в уравнении  дисперсии остатков пропорциональны квадрату объема продукции
дисперсии остатков пропорциональны квадрату объема продукции  .
. После применения обобщенного метода наименьших квадратов новая модель приняла вид
После применения обобщенного метода наименьших квадратов новая модель приняла вид  . Тогда параметр
. Тогда параметр  в новом уравнении характеризует среднее изменение затрат на единицу продукции при увеличении …
в новом уравнении характеризует среднее изменение затрат на единицу продукции при увеличении … – затраты на единицу продукции,
– затраты на единицу продукции,  – фондоемкость продукции,
– фондоемкость продукции,  – трудоемкость продукции. В новой модели параметр
– трудоемкость продукции. В новой модели параметр  показывает среднее изменение затрат на единицу продукции
показывает среднее изменение затрат на единицу продукции 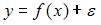 получена диаграмма
получена диаграмма
 на плоскости для зависимости
на плоскости для зависимости  от
от  называется полем корреляции, или диаграммой рассеяния. Поэтому верный ответ – «полем корреляции».
называется полем корреляции, или диаграммой рассеяния. Поэтому верный ответ – «полем корреляции». , и остаточная сумма квадратов отклонений
, и остаточная сумма квадратов отклонений  , то сумма квадратов отклонений, объясненная регрессией, равна …
, то сумма квадратов отклонений, объясненная регрессией, равна …
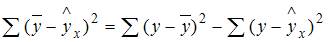
 .
. , где …
, где … на основании 14 наблюдений рассчитаны оценки параметров и записана модель:
на основании 14 наблюдений рассчитаны оценки параметров и записана модель:  (в скобках указаны значения t -статистики соответствующие параметрам регрессии). Известны критические значения Стьюдента для различных уровней значимости
(в скобках указаны значения t -статистики соответствующие параметрам регрессии). Известны критические значения Стьюдента для различных уровней значимости






 формулируется нулевая гипотеза
формулируется нулевая гипотеза  при альтернативной гипотезе
при альтернативной гипотезе  . Затем рассчитывается фактическое значение t -статистики, которое сравнивается с критическим значением Стьюдента
. Затем рассчитывается фактическое значение t -статистики, которое сравнивается с критическим значением Стьюдента  для требуемого числа степеней свободы и уровня значимости. Если
для требуемого числа степеней свободы и уровня значимости. Если  , коэффициент
, коэффициент  значим; если
значим; если  коэффициент
коэффициент 





 которые представляют одну и ту же модель, так как
которые представляют одну и ту же модель, так как  и оба уравнения они отражают гиперболическую зависимость y от x.
и оба уравнения они отражают гиперболическую зависимость y от x.  . Поэтому уравнение
. Поэтому уравнение  может быть применен метод …
может быть применен метод … является внутренне линейной и с помощью логарифмирования может быть преобразована к виду
является внутренне линейной и с помощью логарифмирования может быть преобразована к виду  , которая является линейной относительно логарифмов переменных. Сделав замену переменных
, которая является линейной относительно логарифмов переменных. Сделав замену переменных  ,
,  ,
,  ,
,  , получим линейную функцию
, получим линейную функцию  . Поэтому для линеаризации используется сначала логарифмирование, затем замена переменных.
. Поэтому для линеаризации используется сначала логарифмирование, затем замена переменных. . Коэффициент корреляции между логарифмами исходных показателей составил
. Коэффициент корреляции между логарифмами исходных показателей составил  . Коэффициент детерминации для модели в исходных показателях равен …
. Коэффициент детерминации для модели в исходных показателях равен …
 ,
,  ,
,  .
.  равна …
равна … .
.
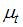 – среднее и
– среднее и  – дисперсия. Если временной ряд является стационарным, то …
– дисперсия. Если временной ряд является стационарным, то …



 ;
;  .
. и спрос
и спрос  являются линейными функциями цены p, состоит из уравнений …
являются линейными функциями цены p, состоит из уравнений …




 ,
,








