Схемы из функциональных элементов
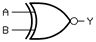
Различают схемы без памяти (комбинационные схемы) и схемы с памятью (последовательные схемы). Одной из математических моделей комбинационных схем являются схемы из функциональных элементов (СФЭ). Другими моделями являются контактные схемы (C. Shannon, 1937) и двоичные решающие диаграммы (C. Lee, 1959). По сути, указанные формализмы являются разными способами представления функций алгебры логики (ФАЛ). Напомним определение СФЭ. Определение. Базисом называется непустое множество функций алгебры логики. Определение. Схемой из функциональных элементов (СФЭ) в базисе B называется размеченный ориентированный граф без циклов, в котором 1) вершины, являющиеся истоками, помечены символами переменных и называются входами (разным вершинам соответствуют разные переменные); 2) каждая вершина, в которую входит k ³ 1 дуг, помечена функцией из базиса B, зависящей от k переменных (такие вершины называются функциональными элементами или вентилями); 3) некоторые вершины выделены как выходы (входные вершины могут быть и выходными). Определение. Сложностью СФЭ называется число входящих в нее ФЭ. Часто в качестве базиса используют {Ù, Ú, Ø}. Соответствующие ФЭ называются дизъюнктором (вентиль ИЛИ), конъюнктором (вентиль И) и инвертором (вентиль НЕ). Графически вентили изображаются следующим образом (стандарт ANSI).
Легко заметить, что для обозначения отрицания используется маленький кружок. Такие кружки можно рисовать не только на выходе вентиля, но и на его входах (если требуется инвертировать соответствующий входной сигнал). Задание. Изобразить графически схемы, реализующие следующие функции: 1) мультиплексор 2-в-1 (if sel then out=in0 else out=in1); 2) мультиплексор 4-в-1. Домашнее задание. Изобразить графически схемы, реализующие следующие функции: 1) демультиплексор 1-в-2 (if sel then out0=in else out1=in); 2) демультиплексор 1-в-4.
|