Методические указания по теме. Задача 1. Имеются следующие данные о возрастном составе студентов группы заочного отделения ВУЗа (лет): 19; 19; 19; 20; 20; 20; 20; 20; 20; 20; 20; 20; 21;
Задача 1. Имеются следующие данные о возрастном составе студентов группы заочного отделения ВУЗа (лет): 19; 19; 19; 20; 20; 20; 20; 20; 20; 20; 20; 20; 21; 21; 21; 22; 23; 23; 24; 25; 25; 25; 26; 27; 29. Для анализа распределения студентов по возрасту требуется: 1) построить интервальный ряд распределения и его график; 2) рассчитать модальный, медианный и средний возраст, установить его типичность с помощью коэффициентов вариации; 3) проверить распределение на нормальность с помощью коэффициентов асимметрии и эксцесса. Решение. Для построения интервального ряда из дискретного используется формула Стерджесса, с помощью которой определяется оптимальное количество интервалов (n): n = 1 +3,322 lg N, (10) где N – число величин в дискретном ряде. В нашей задаче n = 1 + 3,322 lg 25 = 1 + 3,322*1,398 = 5,64. Так как число интервалов не может быть дробным, то округлим его до ближайшего целого числа, т.е. до 6. После определения оптимального количества интервалов определяем размах интервала по формуле: h = H / n, (11) где H – размах вариации, определяемый по формуле (12). H = Хмах –Хmin, (12) где Xмax и Xmin — максимальное и минимальное значения в совокупности. В нашей задаче h = (29 – 19)/6 = 1,67. Интервальная группировка данных приведена в первом столбце таблицы 1, которая содержит также алгоритм и промежуточные расчеты. Таблица 1. Вспомогательные расчеты для решения задачи
На основе этой группировки строится график распределения возраста студентов (рис.2).
Рис.2. График распределения возраста студентов. Мода – это наиболее часто повторяющееся значение признака. Для интервального ряда с равными интервалами величина моды определяется по формуле (13):
где ХMo – нижнее значение модального интервала; fMo – число наблюдений или объем взвешивающего признака (вес признака) в модальном интервале; fMo-1 – то же для интервала, предшествующего модальному; fMo+1 – то же для интервала, следующего за модальным; h – величина интервала изменения признака в группах. В нашей задаче чаще всего повторяется (12 раз) первый интервал возраста (до 20,67), значит, это и есть модальный интервал. Используя формулу (13), определяем точное значение модального возраста: Мо = 19 + 1,667*(12-0)/(2*12-4-0) = 20 (лет). Медиана – это такое значение признака, которое приходится на середину ранжированного ряда. Таким образом, в ранжированном ряду распределения одна половина ряда имеет значения признака больше медианы, другая – меньше медианы. Для интервального ряда с равными интервалами величина медианы определяется так:
где XMe – нижняя граница медианного интервала; h – его величина (размах); В нашей задаче второй интервал возраста (от 20,67 до 22,33) является медианным, так как на него приходится середина ряда распределения возраста. Используя формулу (14), определяем точное значение медианного возраста: Ме = 20,67 + 1,667*(12,5-12)/4 = 20,878 (года). Средняя величина – это обобщающий показатель совокупности, характеризующий уровень изучаемого явления или процесса. Средние величины могут быть простыми и взвешенными. Простая средняя рассчитывается при наличии двух и более статистических величин, расположенных в произвольном (несгруппированном) порядке, по общей формуле (15). Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием общей формулы (16).
При этом обозначено: Xi – значения отдельных статистических величин или середин группировочных интервалов; m - показатель степени, от значения которого зависят виды средних величин. Используя формулы (15) и (16) при разных показателях степени m, получаем частные формулы каждого вида (см. таблицу 2). Таблица 2. Виды степенных средних и их применение
Выбор вида формулы средней величины зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять. Показатель степени m в общей формуле средней величины оказывает существенное влияние на значение средней величины: по мере увеличения степени возрастает и средняя величина (правило мажорантности средних величин), то есть В нашей задаче, применяя формулу (18) и подставляя вместо Коэффициенты вариации рассчитываются как отношение среднего отклонения к средней величине. Поскольку среднее отклонение может определяться линейным и квадратическим способами, то соответствующими могут быть и коэффициенты вариации. Среднее линейное отклонение определяется по формулам (29) и (30):
Среднее квадратическое отклонение определяется как корень квадратный из дисперсии, то есть по формуле (31):
Дисперсия определяется по формулам (32) или (33):
В нашей задаче, применяя формулу (30), определим ее числитель и внесем в расчетную таблицу. В итоге получим среднее линейное отклонение: Л = 54,937/25 = 2,198 (года). Разделив это значение на средний возраст, получим линейный коэффициент вариации: Применяя формулу (33), получим в итоге дисперсию: Д = 164,018/25 = 6,561. Извлечем из этого числа корень и получим в результате среднее квадратическое отклонение: В качестве показателей асимметрии используются: коэффициент асимметрии – нормированный момент третьего порядка (34) и коэффициент асимметрии Пирсона (35):
Если значение коэффициента асимметрии положительно, то в ряду преобладают варианты, которые больше средней (правосторонняя скошенность), если отрицательно – левосторонняя скошенность. Если коэффициент асимметрии равен 0, то вариационный ряд симметричен. В нашей задаче Для характеристики крутизны распределения используется центральный момент 4-го порядка:
Для образования безразмерной характеристики определяется нормированный момент 4-го порядка
Для приближенного определения эксцесса может быть использована формула Линдберга (38):
где В нашей задаче числитель центрального момента 4-го порядка рассчитан в последнем столбце расчетной таблицы. В итоге по формуле (37) имеем: Ex = (2780,498/25)/2,5614–3 = 111,220/43,017–3 = -0,415. Так как Ex<0, то распределение низковершинное. Это подтверждает и приблизительный расчет по формуле (38): в интервале 21,967
|

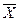


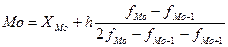 , (13)
, (13) , (14)
, (14) – сумма наблюдений (или объема взвешивающего признака), накопленная до начала медианного интервала; fMe – число наблюдений или объем взвешивающего признака в медианном интервале.
– сумма наблюдений (или объема взвешивающего признака), накопленная до начала медианного интервала; fMe – число наблюдений или объем взвешивающего признака в медианном интервале.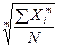 ; (15)
; (15) 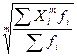 . (16)
. (16) 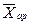 =
=  (17)
(17)
 (18)
(18)
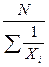 (19)
(19)
 (20)
(20)
 (21)
(21)
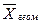
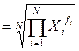 (22)
(22)
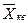 =
= 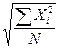 (23)
(23)
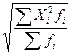 (24)
(24)
 =
= 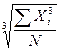 (25)
(25)
 (26)
(26)
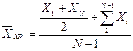 (27)
(27)
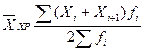 (28)
(28)
 <
<  <
<  <
<  , то
, то 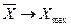 , а если
, а если  , то
, то  .
.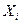 середины интервалов возраста ХИ, определяем средний возраст студентов:
середины интервалов возраста ХИ, определяем средний возраст студентов: 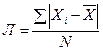 –простое; (29)
–простое; (29) 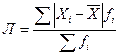 – взвешенное. (30)
– взвешенное. (30)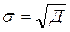 . (31)
. (31) –простая; (32)
–простая; (32)  –взвешенная. (33)
–взвешенная. (33)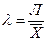 = 2,198/21,967 = 0,100. По значению этого коэффициента для рассмотренной группы студентов делаем вывод о типичности среднего возраста, т.к. расчетное значение коэффициента вариации не превышает критериального (0,100 < 0,333).
= 2,198/21,967 = 0,100. По значению этого коэффициента для рассмотренной группы студентов делаем вывод о типичности среднего возраста, т.к. расчетное значение коэффициента вариации не превышает критериального (0,100 < 0,333). =
=  = 2,561 (года).Разделив это значение на средний возраст, получим квадратический коэффициент вариации:
= 2,561 (года).Разделив это значение на средний возраст, получим квадратический коэффициент вариации: 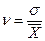 = 2,561/21,967 = 0,117. По значению этого коэффициента для рассмотренной группы студентов можно сделать вывод о типичности среднего возраста, т.к. расчетное значение коэффициента вариации не превышает критериального (0,117 < 0,333).
= 2,561/21,967 = 0,117. По значению этого коэффициента для рассмотренной группы студентов можно сделать вывод о типичности среднего возраста, т.к. расчетное значение коэффициента вариации не превышает критериального (0,117 < 0,333).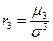 ,(34)
,(34) 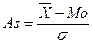 .(35)
.(35) =
=  =383,636/25 = 15,345;
=383,636/25 = 15,345;  =2,5613= 16,797;
=2,5613= 16,797; 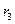 =15,345/16,797 = 0,914 > 0, значит, распределение студентов по росту с правосторонней асимметрией. Это подтверждает и значение коэффициента асимметрии Пирсона: As = (21,967-20)/2,561 = 0,768.
=15,345/16,797 = 0,914 > 0, значит, распределение студентов по росту с правосторонней асимметрией. Это подтверждает и значение коэффициента асимметрии Пирсона: As = (21,967-20)/2,561 = 0,768.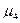 =
= 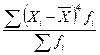 .(36)
.(36)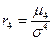 , который и характеризует крутизну (заостренность) графика распределения. При измерении асимметрии эталоном служит нормальное (симметричное) распределение, для которого
, который и характеризует крутизну (заостренность) графика распределения. При измерении асимметрии эталоном служит нормальное (симметричное) распределение, для которого  =3. Поэтому для оценки крутизны данного распределения в сравнении с нормальным вычисляется эксцесс распределения (37):
=3. Поэтому для оценки крутизны данного распределения в сравнении с нормальным вычисляется эксцесс распределения (37):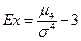 .(37)
.(37)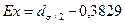 ,(38)
,(38)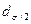 – доля количества вариант, лежащих в интервале, равном половине
– доля количества вариант, лежащих в интервале, равном половине 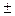 0,5*2,561, то есть от 20,687 до 23,248 находится примерно 21,4% студентов. Таким образом, Ex = 0,214 – 0,3829 = –0,169.
0,5*2,561, то есть от 20,687 до 23,248 находится примерно 21,4% студентов. Таким образом, Ex = 0,214 – 0,3829 = –0,169.


