Расчет статистических показателей
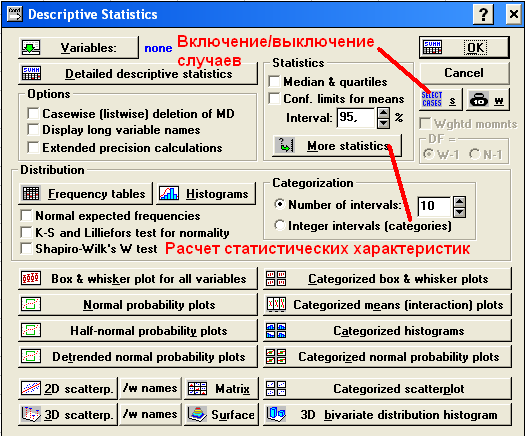
Расчет основных статистических показателей проводиться в модуле Basic Statistic. Из статистических процедур следует выбрать Descriptive statistics (Описательные статистики). Чтобы выбрать статистики, подлежащие вычислению, в окне Descriptive statistics (Описательные статистики) следует воспользоваться кнопкой More statistics (Большинство статистических характеристик) (рис. 1).
Рисунок 1. Кнопка для указания статистических характеристик После нажатия этой кнопки появится окно, в котором следует указать статистические характеристики, подлежащие расчету (рис. 2). Указание характеристик производится путем проставления флажка напротив подлежащей вычислению характеристики. Чтобы выбрать все предложенные для расчета характеристики, необходимо нажать кнопку All.
Рисунок 2. Выбор статистических характеристик, подлежащих вычислению На рисунке 2: Valid N - объем выборки; Mean - средняя арифметическая; Среднее значение случайной величины представляет собой наиболее типичное, наиболее вероятное ее значение, своеобразный центр, вокруг которого разбросаны все значения признака. Sum - сумма; Median - медиана; Медианой является такое значение случайной величины, которое разделяет все случаи выборки на две равные по численности части. Standard Deviation - стандартное отклонение; Стандартное отклонение (или среднее квадратическое отклонение) является мерой изменчивости (вариации) признака. Оно показывает, на какую величину в среднем отклоняются случаи от среднего значения признака. Особенно большое значение имеет при исследовании нормальных распределений. В нормальном распределении 68% всех случаев лежит в интервале + одного отклонения от среднего, 95% - + двух стандартных отклонений от среднего и 99,7% всех случаев - в интервале + трех стандартных отклонений от среднего. Variance - дисперсия; Дисперсия является мерой изменчивости, вариации признака и представляет собой средний квадрат отклонений случаев от среднего значения признака. В отличии от других показателей вариации дисперсия может быть разложена на составные части, что позволяет тем самым оценить влияние различных факторов на вариацию признака. Дисперсия - один из существеннейших показателей, характеризующих явление или процесс, один из основных критериев возможности создания достаточно точных моделей. Standard error of mean - стандартная ошибка среднего; Стандартная ошибка среднего это величина, на которую отличается среднее значение выборки от среднего значения генеральной совокупности при условии, что распределение близко к нормальному. С вероятностью 0,68 можно утверждать, что среднее значение генеральной совокупности лежит в интервале + одной стандартной ошибки от среднего, с вероятностью 0,95 - в интервале + двух стандартных ошибок от среднего и с вероятностью 0,99 - среднее значение генеральной совокупности лежит в интервале + трех стандартных ошибок от среднего. 95% confidence limits of mean - 95%-ый доверительный интервал для среднего; Интервал, в который с вероятностью 0,95 попадает среднее значение признака генеральной совокупности. Minimum, maximum - минимальное и максимальное значения; Lower, upper quartiles - нижний и верхний квартили; Верхний квартиль это такое значение случайной величины, больше которого по величине 25% случаев выборки. Верхний квартиль это такое значение случайной величины, меньше которого по величине 25% случаев выборки. Range - размах; Расстояние между наибольшим (maximum) и наименьшим (minimum) значениями признака. Quartile range - интерквартильная широта; Расстояние между нижним и верхним квартилями. Skewness -асимметрия; Асимметрия характеризует степень смещения вариационного ряда относительно среднего значения по величине и направлению. В симметричной кривой коэффициент асимметрии равен нулю. Если правая ветвь кривой, начиная от вершины) больше левой (правосторонняя асимметрия), то коэффициент асимметрии больше нуля. Если левая ветвь кривой больше правой (левосторонняя асимметрия), то коэффициент асимметрии меньше нуля. Асимметрия менее 0,5 считается малой. Standard error of Skewness -стандартная ошибка асимметрии; Kurtosis - эксцесс; Эксцесс характеризует степень концентрации случаев вокруг среднего значения и является своеобразной мерой крутости кривой. В кривой нормального распределения эксцесс равен нулю. Если эксцесс больше нуля, то кривая распределения характеризуется островершинностью, т.е. является более крутой по сравнению с нормальной, а случаи более густо группируются вокруг среднего. При отрицательном эксцессе кривая является более плосковершинной, т.е. более пологой по сравнению с нормальным распределением. Отрицательным пределом величины эксцесса является число -2, положительного предела - нет. Standard error of Kurtosis - стандартная ошибка эксцесса. Напротив статистических характеристик, подлежащих вычислению, следует поставить флажок. После нажатия на кнопку OK окна Descriptive statistics на экране появится таблица с результатами расчетов описательных статистик (рис. 3).
Рисунок 3. Рассчитанные статистические характеристики К сожалению, пакет STATISTICA не рассчитывает такие часто применяемые статистики, как коэффициент вариации и относительная ошибка среднего значения (точность опыта). Однако их определение не представляет большого труда. Коэффициент вариации (%) есть отношение стандартного отклонения к среднему значению, умноженное на 100%:
Коэффициент вариации, как дисперсия и стандартное отклонение, является показателем изменчивости признака. Коэффициент вариации не зависит от единиц измерения, поэтому удобен для сравнительной оценки различных статистических совокупностей. При величине коэффициента вариации до 10% изменчивость оценивается как слабая, 11-25% - средняя, более 25% - сильная. Относительная ошибка среднего значения (%) - отношение стандартной ошибки среднего к среднему значению, умноженное на 100%:
Чтобы вычислить другие специфические статистические показатели (мода, среднее геометрическое, гармоническое и т.д.) необходимо выбрать модуль Nonparametric Statistics (Непараметрическая статистика),статистическая процедура Ordinal descriptive statistics (Порядковая описательная статистика). Кнопка Select cases (Выбор случаев) (рис. 1) позволяет поставить условия включения (include if) или исключения (exclude if) случаев (строк файла данных) из статистической обработки. После нажатия этой кнопки появляется окно Case Selection Conditions (Условия выбора случаев), в котором следует указать случаи, исключающиеся из статистической обработки (рис. 4). Операторы, которые могут использоваться при написании выражений, а также примеры самих выражений имеются непосредственно на самом диалоговом окне Case Selection Conditions (Условия выбора случаев) в нижней его части (рис. 4).
Рисунок 4. Окно Case Selection Conditions (Условия выбора случаев) Для визуализации описательных статистик (статистических характеристик) можно построить статистические графики типа коробок. Это делается при помощи кнопки Box & Whisker plot for all variable окна Descriptive statistics (рис. 1). На графике можно отобразить статистики, установив переключатель в одно из 4-х положений (рис. 5):
Рисунок 5. Окно для выбора описательных статистик На рисунке 5: Median/Quart./Range - Медиана / Квартили / Размах; Mean/SE/SD - Среднее / Ошибка среднего / Стандартное отклонение; Mean/SD/1.96SD - Среднее / Стандартное отклонение / Интервал 1,96* стандартного отклонения; Mean/SE/1.96*SE - Среднее /Ошибка среднего /Интервал 1,96 * ошибки среднего. На рисунке 6 показан произвольный график коробок, построенный дляпеременной масса.
Рисунок 6. График коробок
|



 . (1)
. (1) . (2)
. (2)





