Машины Тьюринга
Исторически понятие конечного автомата развилось из близкого понятия, введенного в 1936 году логиком Тьюрингом. Тьюринг рассматривал гипотетическую ╚машину╩, имеющую конечное множество S внутренних состояний и одну бесконечно длинную ленту, разделенную на ячейки, которую машина могла передвигать на одну ячейку вправо или влево за такт. В каждой ячейке машина может записывать символ из конечного алфавита A. Первоначально лента должна быть пустой, кроме конечного числа ячеек заполненных заранее. (Эти заранее заполненные ячейки можно представлять себе как программу запуска машины.) Основная разница между машиной Тьюринга и конечным автоматом состоит в том, что: 1) лента машины Тьюринга бесконечна; 2) машина Тьюринга может двигаться вдоль ленты (или смещать ленту) в любом направлении. Это придает машине бесконечную память, которую можно использовать в ходе вычислений. Сверх того, каждую ячейку можно просматривать многократно. Формальное определение машины Тьюринга существует в нескольких вариантах. Вот один из них. Определение. Машиной Тьюринга называется пятерка объектов [ A, S, n, z, d] следующего типа. A есть конечный алфавит символов, которые могут быть записаны в ячейках и являются одновременно входными и выходными: A = { a 0, a 1,..., an }. S есть конечное множество внутренних состояний S = { s 0, s 1,..., sr }; n - функция из S ╢ A в S; z - функция из S ╢ A в A; d - функция из S ╢ A в {П, Л, ОСТАНОВ}, интуитивный смысл которого станет ясен из дальнейшего. Машина Тьюринга работает следующим образом. Она начинает работу, находясь в начальном состоянии s 0. После считывания первого символа она переходит в новое внутреннее состояние, определяемое функцией n, записывает в ячейке символ, являющийся значением функции z, перемещает ленту направо (П), налево (Л), или остается на месте и прекращает работу (ОСТАНОВ) в зависимости от значения функции d.
На рисунке схематически изображена лента машины Тьюринга и считывающая-записывающая головка. Таким образом, работа машины состоит в повторении следующего цикла: считывание символа из ячейки, впечатывание нового символа, выбор которого определяет функция z, в эту ячейку (может оказаться, что это тот же символ), сдвиг ленты направо или налево либо остановка. Лента бесконечна в обоих направлениях, однако вначале (и, значит, после любого такта) заполнено лишь конечное число ячеек. Пример. Машина Тьюринга, описанная ниже, считывает входную последовательность нулей и единиц, выпечатывает Ч, если число единиц четное, и Н, если нечетно. Строке из нулей и единиц предшествуют и последуют пустые ячейки, обозначаемые #. Символы Ч или Н печатаются в первой пустой ячейке вслед за входной строкой. Алфавит, таким образом, имеет вид A = {#, 0, 1, Ч, Н}. Внутренние состояния: S = { s 0, s 1, s 2}; s 0 - начальное состояние. Машина останавливается по сигналу ОСТАНОВ. n: (s 0, 0) a s 1 z: (s 0, 0) a 0 d: (s 0, 0) a Л (s 0, 1) a s 2 (s 0, 1) a 1 (s 0, 1) a Л (s 1, 0) a s 1 (s 1, 0) a 0 (s 1, 0) a Л (s 1, 1) a s 2 (s 1, 1) a 1 (s 1, 1) a Л (s 2, 0) a s 2 (s 2, 0) a 0 (s 2, 0) a Л (s 2, 1) a s 1 (s 2, 1) a 1 (s 2, 1) a Л (s 0,#) a s 0 (s 0, #) a # (s 0, #) a Л (s 1,#) a s 1 (s 1, #) a Ч (s 1, #) a ОСТАНОВ (s 2,#) a s 2 (s 2, #) a Н (s 2, #) a ОСТАНОВ Удобнее задавать функции n, z, d, пользуясь обозначениями Тьюринга. В этом варианте машина Тьюринга задается конечным множеством пятерок [ si, aj, sr, zl, tn ]. В каждой такой пятерке si - текущее состояние машины; aj - символ, считываемый из ячейки: sr - следующее состояние машины, sr = n (si, aj); zl - символ, печатаемый в ячейке, zl = z (si, aj); tn - одна из команд П, Л, ОСТАНОВ. В этих обозначениях описанная выше машина задается так:
Теорема. Пусть M = [ A, S, Z, n, z] - некоторый конечный автомат. Положим
(L - символ пустой ячейки) и
для всех
Предыдущий раздел Оглавление Следующий раздел
|
П 
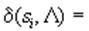ОСТАНОВ
. Тогда машина Тьюринга 
ставит в соответствие входным строкам те же выходные строки, что и M. 
