Рандомизованные деревья
Варианты данных в структурах:
1. В записной книжке указаны фамилии и номера телефонов 10 человек. Определить телефон человека с заданной фамилией. Удалить запись о человеке с заданной фамилией. 2. Известны фамилия и вес каждого из 10 человек. Вывести вес человека с заданной фамилией. Удалить данные о человеке с заданной фамилией. 3. Известны данные о стоимости каждой из 10 моделей автомобилей. Вывести стоимость заданной модели автомобиля. Удалить данные о заданной модели автомобиля. 4. Известны данные о численности населения и площади 10 государств. Определить плотность заданного государства. Удалить данные о заданном государстве. 5. Известны данные о массе и объеме 10 тел, изготовленных из различных материалов. Определить плотность заданного материала. Удалить данные о заданном материале. 6. Даны названия 10 городов и стран, в которых они находятся. Вывести название страны, в которой расположен заданный город. Удалить данные о заданном городе. 7. Известны данные о 10 сотрудниках фирмы (фамилия, зарплата). Вывести зарплату заданного сотрудника. Удалить данные о заданном сотруднике.
Лабораторная работа № 6 Рандомизованные деревья
Количество операций для процедур добавления, удаления и поиска в двоичном дереве поиска определяется высотой дерева. Высота будет минимальной, равной log 2 n, если элементы дерева будут распределены по нему равномерно, то есть дерево будет идеально сбалансированным. На практике очень сложно добиться идеальной сбалансированности, но существует много способов достичь приближенной сбалансированности. Наиболее известны АВЛ-деревья, предложенные Г.М. Адельсоном-Вельским и Е.М. Ландисом; красно-черные деревья; 2–3 деревья, разработанные Хопкрофтом. Во всех перечисленных структурах поиск производится так же, как в обычных деревьях двоичного поиска, а при добавлении и удалении с помощью специальных операций, называемых вращениями, производится перестройка дерева с целью добиться лучшей сбалансированности. Рассмотрим наиболее простой вариант приближенно сбалансированных деревьев – рандомизованные деревья. Заметим, что наименее сбалансированным получается дерево, элементы в которое добавляются в отсортированном порядке (рисунок 8.3 в предыдущей лабораторной работе). Поэтому при добавлении в дерево данных, упорядоченных случайным образом, получится дерево, близкое к сбалансированному. Так как заранее невозможно предсказать, насколько отсортированы добавляемые данные, то будем добиваться сбалансированности дерева, иногда добавляя элементы в корень дерева, а не в его лист. Так, если в дерево добавляется n элементов, то вероятность для каждого элемента оказаться при случайном упорядочении первым и попасть в корень дерева равна 1/ n. Используя генератор случайных чисел, с такой вероятностью и будем помещать элемент в корень рандомизованного дерева. Для определения вероятности требуется знать количество элементов в каждом поддереве. Будем хранить это количество в корне поддерева в поле count и изменять его при добавлении и удалении элементов. Получим следующую структуру данных для хранения узла дерева:
Для работы с рандомизованными деревьями необходимо разработать следующие функции:
Рассмотрим все эти функции подробнее. Для определения количества элементов в поддереве напишем функцию get_count, правильно работающую и с пустыми деревьями:
<если> <t – пусто> <то> <вернуть> 0 <иначе> <вернуть> t.n
Далее необходимо написать процедуру для вставки элемента в корень дерева. Процедура будет рекурсивной: для пустого дерева она просто создаст новый узел, для непустого – рекурсивно добавит узел в корень левого или правого поддерева, а затем выполнит левое или правое вращение, чтобы «поднять» этот добавленный элемент в корень исходного дерева. Например, добавим число 2 в корень дерева, содержащего элементы 1, 3 и 5:
Процедура добавления элемента в корень рандомизованного дерева отличается от процедуры добавления, приведенной в предыдущей лабораторной работе, наличием поворотов (вращений) после добавления элемента в правое или левое поддерево и модификацией поля, хранящего количество элементов в поддереве: <если> (t - пусто) <то> t=new t.data = x t.left = t.right = 0 t.count = 1 <иначе> <если> x<t.data <то> add (t.left,x) t.cоunt = t.cоunt + 1 <левый поворот>; <иначе> add (t.right,x) t.cоunt = t.cоunt + 1 <правый поворот>;
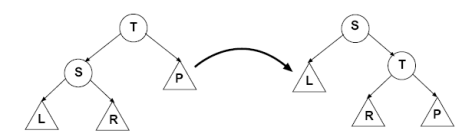
Рассмотрим подробнее левое вращение (поворот), то есть операцию, которая корень левого поддерева делает корнем дерева в целом. Обозначим указатель на корень дерева T, на корень левого поддерева S. Для того, чтобы дерево осталось двоичным деревом поиска, необходимо, чтобы правое поддерево S (на рисунке обозначено буквой R) стало левым поддеревом T. Наглядно левое вращение показано на рисунке:
Рисунок 9.2 – Левое вращение
Процедура левого вращения rot_l с обновлением поля count выглядит так: s=t.left; n1=get_count(t) n2=get_count(s.right)+get_count(t.right)+1; t.left=s.right; s.right=t; s.count=n1; t.count=n2; t=s Аналогично выполняется правое вращение rot_r. Процедура добавления элемента add должна вызывать добавление в корень с вероятностью 1/n. Для этого вычисляется случайное число от 0 до n, и добавление в корень происходит, если оно равно 0. Напомним, что в языке программирования Pascal такое случайное число вычисляется с помощью функции random(n), а в языке программирования С++ с помощью выражения rand()%n. Запишем процедуру добавления элемента в дерево: r = <случайное число от 0 до get_count(t)> <если> r = 0 <то> add_root(t,x) <иначе> <если> x<t.data <то> add(t.left,x) <иначе> add(t.right,x) t.count = t.count +1
Удаление элемента из рандомизованного дерева также должно сохранять сбалансированность. Поэтому всегда заменять удаляемый элемент на наименьший элемент из правого поддерева, как в предыдущей лабораторной работе, нельзя. Если одно из поддеревьев содержит больше элементов, то разумно, чтобы элемент для замены удаляемого извлекался с большей вероятностью именно из этого поддерева. Удаление в рандомизованном дереве основано на операции объединения деревьев. После удаления элемента необходимо объединить его левое и правое поддеревья. Объединение деревьев выполняется рекурсивно: если одно из деревьев пусто, то результат объединения равен другому дереву; если оба дерева не пусты, то в корень объединенного дерева помещаем либо корень левого дерева и присоединяем справа объединение его правого поддерева и второго дерева, либо корень правого дерева и аналогично другое дерево присоединяем слева (см. рисунок 9.3):
Рисунок 9.3 – Объединение деревьев Пусть левое дерево содержит <если> <r– пусто> <то> <вернуть> l <иначе> <если> <l– пусто> <то> <вернуть> r <иначе> n=get_count(r)+get_count(l) s=<случайное число от 0 до n> <если> s<get_count(l) <то> l.right=join(l.right,r); l.count=n; <вернуть> l <иначе> r.left=join(l,r.left); r.count=n; <вернуть> r
Теперь запишем процедуру del удаления элемента с ключом x из рандомизованного дерева t. В процедуре будем использовать логический параметр find, который нужен для сохранения информации о том, что элемент найден, чтобы скорректировать количество элементов в вышестоящих узлах: find = <ложь> <если> <t - не пусто> <то> <если> x<t.data <то> del(t.left,x,find) <если> find <то> t.count = t.count-1 <иначе> <если> x>t.data <то> del(t.right,x,find) <если> find <то> t.count = t.count-1 <иначе> { то есть найден элемент для удаления} s=t t=join(t.left,t.right) <очищение памяти от s> find = <истина>
Поиск элемента и обход дерева осуществляются теми же процедурами, что для обычных двоичных деревьев. Можно показать, что процедуры добавления, удаления и поиска для рандомизованных деревьев выполняются за порядка log 2 n операций.
|

 (а)
(а)
 (б)
(б)
 (в)
(в)
 (г)
(г)

 узлов, а правое
узлов, а правое  узлов. Тогда корень объединения будем выбирать из левого дерева с вероятностью
узлов. Тогда корень объединения будем выбирать из левого дерева с вероятностью 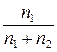 , а из правого – с вероятностью
, а из правого – с вероятностью  . Приведем функцию join объединения деревьев l и r:
. Приведем функцию join объединения деревьев l и r:


