Основные положения. На свариваемый материал процесс дуговой сварки оказывает сильное тепловое воздействие, которое обусловливает структурные и фазовые превращения металла шва и
На свариваемый материал процесс дуговой сварки оказывает сильное тепловое воздействие, которое обусловливает структурные и фазовые превращения металла шва и околошовной зоны. Степень неоднородности металла, вызываемая этими явлениями, снижает механические свойства сварного соединения в целом. Тепловое состояние наиболее полно описывается температурным полем, которое в условиях сварки является нестационарным:
где Т – температура в точке с декартовыми координатами x, y, z в момент времени t. Наиболее полно такое температурное поле, характеризующееся при дуговой сварке высокими скоростями нагрева, охлаждения и градиентом температур, можно теоретически исследовать решением соответствующей краевой задачи дифференциального уравнения теплопроводности [1], [5]. Для решения задач теплопроводности, применительно к дуговой сварке, можно использовать аналитические методы – интегральных преобразований и метод источников (функций Грина), а также численные – метод конечных разностей, конечных элементов и другие. Наиболее простым и удобным для оценки температурных полей при воздействии подвижных источников тепла является предложенный Томсоном метод источников, схематизированный применительно к дуговой сварке и доведенный до простых аналитических зависимостей Н.Н. Рыкалиным. В контрольной работе для оценки температурного поля в массивном изделии при наплавке на его поверхность прямолинейного валика используется схема мощного быcтродвижущегося точечного источника на полубесконечном теле [1]. При этом предполагается, что источник теплоты, движущийся прямолинейно по поверхности полубесконечного тела, имеет бесконечно большую тепловую мощность q и скорость движения u, но конечную погонную энергию q п:
(2)
Остальные допущения являются общими для метода источников – независимость теплофизических свойств от температуры, отсутствие учета теплоты фазовых переходов и др. [1]. При выполнении этих допущений температура в точке с координатами (у, z) в момент времени t определяется по формуле (1)
(3)
Где Для расчета изотерм в уравнении (3) необходимо сделать замену
(4)
Для изотермы в плоскостях ХОY (на поверхности изделия) уравнение (4) упростится:
(5)
где x <0. С помощью неявного задания функции
Рис. 1 Температурное поле мощности быстродвижущего точечного источника на полубесконечном теле: а – основные обозначения; б, в – изотерма Т = Т 0 в плоскости XОY и ZOY соответственно. Вторую точку пересечения изотермы с осью ОХ (точку В,рис. 1, a) легко найти из (5), положив y 0= 0:
(6)
где L при Предварительно следует продифференцировать
(7)
(8)
Очевидно, что максимальная ширина любой изотермы
(9) а в хвостовой:
(10)
Абсциссы точек изотерм удобно задавать в виде массива { хi }, i =1, 2,..., (2 n +1), где
Рассчитав массив абсцисс { xi }, легко по формуле (5) вычислить соответствующий массив ординат { y i}, i =1, 2,..., 2n+1, где у 1= 0,..., у 2n+1= L,
(12)
Очевидно, что ординаты точек yi при одних и тех же абсциссах хi, на ветвях АСВ и АDВ будут различаться лишь знаками (рис. 1, б). Таким образом, имея основные параметры режима сварки I, U и u, зная теплофизические свойства свариваемого металла и задавшись интересуемой температурой T 0, по формулам (6), (7), (11) следует найти { xi }, а по формулам (8), (12) – { yi }. Это позволит, задавшись масштабом, найти точки { xi, yi } в системе координат ХОY и построить очертания контура изотерм T 0. Термические циклы при сварке можно определить в точках, лежащих на поверхности свариваемого изделия и расположенных на перпендикуляре к оси движения источника у I, y II, y III(рис. 1. а). Тогда в формуле (3) z= 0 и
(13)
Общий вид графика термического цикла представлен на рис. 2.
Рис. 2. Определение скорости охлаждения металла по заданному термическому циклу методом графического дифференцирования.
Продифференцировав выражение (13) по времени и применив необходимое условие максимума, находим время tm, достижения максимальной температуры Тm [2]:
(14)
График проходит через начало координат, так как при t ®0 и
(15)
где n =3... 5 и t 0=0, t 1= ht, t 2=2 ht,..., tn=tm. На нисходящей ветви шаг следует выбрать переменным нарастающим, например:
(16)
Таким образом, для построения термического цикла в заданной точке yN необходимо по формулам (14) рассчитать величины tm и Tm, по формулам (15, 16) сформировать массив абсцисс { ti } и по нему с помощью (13) рассчитать массив ординат { Tj }. Важной характеристикой термического цикла сварки является скорость охлаждения металла в заданной точке Н. Н. Рыкалиным получена формула для вычисления скорости охлаждения металла в точках, лежащих на оси шва при выбранной температуре T:
(17)
где T н – начальная температура свариваемого изделия. Т а б л и ц а 1
Варианты и исходные данные
Формула (17) справедлива при наплавке валика на массивное тело для схемы мощного точечного быстродействующего источника, см. формулу (3). При необходимости рассчитать v в точке, не лежащей на оси при заданной температуре T 1, можно воспользоваться графическим дифференцированием графика термического цикла в этой точке (рис. 2).
(18) Задача 1. По описанному выше алгоритму рассчитать координаты точек изотерм Т (х, у, z) =Т 0 и построить ее контур для случая наплавки под флюсом валика на массивный лист из низкоуглеродистой стали. На рисунке указать длину и ширину изотерм. Вариант режима наплавки и значения температур изотерм студенты выбирают из табл. 1 в соответствии с шифром. Задача 2. Рассчитать и построить термический цикл металла околошовной зоны в точке у 0. Определить время пребывания металла в указанной точке выше температуры Т =0,8 T max, рассчитать скорость охлаждения металла при этой температуре на оси шва и в точке у 0 (варианты и исходные данные приведены в табл. 1). Указания. Расчеты целесообразно проводить с использованием компьютера. При составлении программы следует вначале предусмотреть вычисление постоянных величин, входящих в формулы, а исходные данные (абсциссы точек изотерм, значения времени, при которых определяется температура) и результаты (ординаты точек изотерм и значения температуры) лучше формировать в виде массивов чисел.
|

 (1)
(1)

 –тепловая мощность дуги; l – коэффициент теплопроводности;
–тепловая мощность дуги; l – коэффициент теплопроводности;  – коэффициент температуропроводности; t – время, отсчитанное с момента прохождения дугой проекции исследуемой точки на ось x; I, U –ток и напряжение на дуге: h и – эффективный КПД дуги, равный 0,8... 0,9 для автоматической сварки под флюсом. Система координат (x, y, z) является мгновенно неподвижной, начало ее совпадает с положением источника тепла в данный момент времени. Формула (3) позволяет рассчитать как термические циклы сварки – зависимость температуры от времени
– коэффициент температуропроводности; t – время, отсчитанное с момента прохождения дугой проекции исследуемой точки на ось x; I, U –ток и напряжение на дуге: h и – эффективный КПД дуги, равный 0,8... 0,9 для автоматической сварки под флюсом. Система координат (x, y, z) является мгновенно неподвижной, начало ее совпадает с положением источника тепла в данный момент времени. Формула (3) позволяет рассчитать как термические циклы сварки – зависимость температуры от времени  в заданной точке (координаты у и z фиксированы), так и изотермы
в заданной точке (координаты у и z фиксированы), так и изотермы  где T 0 – заданная температура в фиксированный момент времени. Последние наиболее удобно строить в координатных плоскостях YOZ и ХОY или им параллельных (рис. 1). Контур изотермы
где T 0 – заданная температура в фиксированный момент времени. Последние наиболее удобно строить в координатных плоскостях YOZ и ХОY или им параллельных (рис. 1). Контур изотермы  пл в плоскости (ХОY) в первом приближении можно принять за очертания сварочной ванны.
пл в плоскости (ХОY) в первом приближении можно принять за очертания сварочной ванны. . Наличие знака минус связано с тем, что в схемах быстродействующих источников учитывается распространение тепла только позади движущегося источника, т. е. при отрицательных значениях x. Тогда уравнение изотермической поверхности в неявной форме, соответствующее температуре T 0, примет вид:
. Наличие знака минус связано с тем, что в схемах быстродействующих источников учитывается распространение тепла только позади движущегося источника, т. е. при отрицательных значениях x. Тогда уравнение изотермической поверхности в неявной форме, соответствующее температуре T 0, примет вид:

 , решая (5), можно легко построить контур изотермы Т 0. Можно показать, что при
, решая (5), можно легко построить контур изотермы Т 0. Можно показать, что при  имеем
имеем  , т. е. контур изотермы асимптотически проходит через начало координат, хотя в самой точке действия дуги температура неопределенна (бесконечна).
, т. е. контур изотермы асимптотически проходит через начало координат, хотя в самой точке действия дуги температура неопределенна (бесконечна).

 пл является расчетной длиной сварочной ванны. Точку, соответствующую максимальной ширине изотермы Т 0 (x max, y max) легко найти, воспользовавшись необходимым условием экстремума.
пл является расчетной длиной сварочной ванны. Точку, соответствующую максимальной ширине изотермы Т 0 (x max, y max) легко найти, воспользовавшись необходимым условием экстремума. как функцию, заданную неявно выражением (5):
как функцию, заданную неявно выражением (5):

 . В первом приближении контур изотермы задается четырьмя точками
. В первом приближении контур изотермы задается четырьмя точками  , В (– L, 0), С (x max, – y max) и D (х max, y max), как показано на рис. 1, а, б. Для более точного построения изотермы следует задать несколько промежуточных точек в головной части (АСD) и хвостовой (СВD). Хвостовая часть более вытянута по сравнению с головной. Целесообразно задавать в этих частях одинаковое количество n промежуточных точек. Тогда шаг между соседними точками в головной части составит:
, В (– L, 0), С (x max, – y max) и D (х max, y max), как показано на рис. 1, а, б. Для более точного построения изотермы следует задать несколько промежуточных точек в головной части (АСD) и хвостовой (СВD). Хвостовая часть более вытянута по сравнению с головной. Целесообразно задавать в этих частях одинаковое количество n промежуточных точек. Тогда шаг между соседними точками в головной части составит:


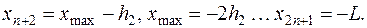 (11)
(11)



 в то же время ось абсцисс является асимптотой графика. Для построения графика термического цикла, точки (на восходящей и нисходящей ветвях) следует располагать с разными шагами по оси абсцисс. На восходящей ветви шаг по времени ht удобно выбрать:
в то же время ось абсцисс является асимптотой графика. Для построения графика термического цикла, точки (на восходящей и нисходящей ветвях) следует располагать с разными шагами по оси абсцисс. На восходящей ветви шаг по времени ht удобно выбрать:


 . Если свариваемая сталь имеет склонность к закалке, то, рассчитав скорость охлаждения по заданному режиму сварки, можно предсказать образование закалочных структур и ширину зоны их залегания.
. Если свариваемая сталь имеет склонность к закалке, то, рассчитав скорость охлаждения по заданному режиму сварки, можно предсказать образование закалочных структур и ширину зоны их залегания.

 Температура T 0, ° C
Температура T 0, ° C




