смешанный процент
ГЛАВА II. НАРАЩЕНИЕ ДЕНЕЖНЫХ СУММ
Содержание:
Оценка доходности инвестиций???????
|
| 2.1. Наращение по простой ставке процентов. Ставка доходности краткосрочных финансовых операций
| | PV – англ. present value –современная ценность,
текущая стоимость.
FV – англ. future value – б удущая стоимость, конечная стоимость.
| Пусть задана исходная (современная) стоимость денегPV. При наращении простых процентов по ставке  за период – каждая следующая сумма больше предыдущей на долю за период – каждая следующая сумма больше предыдущей на долю  от начальной суммы, т.е. на от начальной суммы, т.е. на  .
Наращенную (будущую) сумму денег через .
Наращенную (будущую) сумму денег через  периодов обозначим периодов обозначим  . Тогда, . Тогда,
| к концу 1- промежутка:
| 
| | к концу 2- промежутка:
| 
| | к концу 3- промежутка:
| 
| | …………………..
| ………………………………………………….
| | к концу n- промежутка:
| 
| Последовательность наращенных сумм: 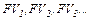 есть арифметическая прогрессия с начальным членом есть арифметическая прогрессия с начальным членом  и разностью и разностью  . .
Таким образом, получили формулу для вычисления наращенной сумму денег по простой ставке  через через  периодов: периодов:
| |
|  , ,
| (2.1.1)
| | I – англ. interest–
сумма процентных денег.
|   сумма процентных денег, начисленных за все процентные периоды n: сумма процентных денег, начисленных за все процентные периоды n:
| 
| (2.1.2)
| | Формула (2.1.1) отражает смысл практических расчётов, связанных с исчислением:
Ø Суммы погашения ссуды, предоставленной под простые проценты;
Ø Размера срочного вклада с процентами.
| |
| Пример 2.1.1.Кредит в размере 100 тыс. руб. выдан на 2 года под 10% годовых. Определите подлежащую возврату сумму, если простой процент начисляется за каждый год, а долг гасится единовременным платежом.
| |
| 
| 
| |
| Ответ: подлежащая возврату сумма составляет 120 000 руб.
| t– англ. англ. time–время.
 – англ. Year–
год. – англ. Year–
год.
| Но такого вида вычисления встречаются редко. Для подобных вычислений чаще пользуются формулой, отражающей принцип расчёта для случаев, когда задана годовая ставка, а срок операции выражен в днях, реже – в месяцах.
Обозначим срок операции через  . Для перевода срока финансовой операции в доли от года используют уравнивающий знаменатель . Для перевода срока финансовой операции в доли от года используют уравнивающий знаменатель  , обозначающий продолжительность года, выраженную в тех же единицах, что и , обозначающий продолжительность года, выраженную в тех же единицах, что и  . Отношение . Отношение 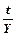 подставим вместо подставим вместо  и получим формулу, которая наиболее часто применяется и является разновидностью Формулы (2.1.1): и получим формулу, которая наиболее часто применяется и является разновидностью Формулы (2.1.1):
| |
|  , ,
| (2.1.3)
| | По вкладам и кредитам на короткий срок, обычно до года, банки, как правило, начисляют простой процент.
| где  время между покупкой и продажей актива в днях (месяцах); время между покупкой и продажей актива в днях (месяцах);
 - количество дней в году (месяцах); - количество дней в году (месяцах);
 цена покупки актива; цена покупки актива;
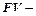 цена продажи актива. цена продажи актива.
  сумма процентных денег, начисленных за время между покупкой и продажей актива: сумма процентных денег, начисленных за время между покупкой и продажей актива:
|
| 
| (2.1.4)
| |
| Формула 2.1.3. используется:
Ø при определении абсолютной величины процентов и наращенной суммы в целом при обслуживании вкладов до востребования;
Ø при обслуживании текущих счетов;
Ø при расчёте суммы долга с процентами при сроке операции менее года и погашения долга единовременным платежом;
Ø при замене и консолидации краткосрочных платежей;
Ø при определении размера процентных платежей при составлении планов погашения задолженности (амортизации).
Заметим, что  и и  в случае измерения их в днях могут быть выражены точно или приближенно (Таблица 1.2.1.). в случае измерения их в днях могут быть выражены точно или приближенно (Таблица 1.2.1.).
| | Actual over
|
| Точное t
фактическое число дней за период
| Приближенное t
-число дней во всех месяцах принимается равным 30.
| |
| Точное Y
фактически дней в году 364 или 365
| Правило (ACT/ACT).
В России по такому принципу ведутся все банковские операции. Этот метод используется многими банками США и Великобритании.
|
| |
| Приближенное Y число дней в году берётся равным 360
| Правило (ACT/360). Распространено во Франции, Бельгии, Испании, Швейцарии, Югославии.
| Правило (30/360). Обычно используют в США, Германии, Дании, Швеции и многих других странах.
| |
| Для точного измерения  пользуются специальной таблицей порядковых номеров дней в году: из номера дня окончания операции вычитают день её начала Как правило, день выдачи и день погашения ссуды считаются за один. Таблица порядковых номеров дней в году приведена в Приложении 1.
Следует учитывать, что применение различных методов подсчёта дней и годовой базы приводят к различным результатам.
Пример.Депозит размером 100 тыс. руб. размещён под 10% годовых с 1.01. по 01.04 текущего года. Начислить проценты по всем трём правилам. пользуются специальной таблицей порядковых номеров дней в году: из номера дня окончания операции вычитают день её начала Как правило, день выдачи и день погашения ссуды считаются за один. Таблица порядковых номеров дней в году приведена в Приложении 1.
Следует учитывать, что применение различных методов подсчёта дней и годовой базы приводят к различным результатам.
Пример.Депозит размером 100 тыс. руб. размещён под 10% годовых с 1.01. по 01.04 текущего года. Начислить проценты по всем трём правилам.
| |
| 
|  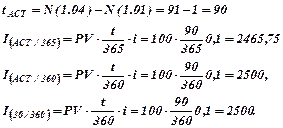
| |
| Пример 2.1.2. Кредит в 100 тыс. руб. взят под 12% годовых 10 сентября. Кой величины достигнет сумма долга к 15 декабря.
| |
| 
| 
| |
| Ответ: сумма долга составит 103200 руб..
| |
| Ставка доходности по краткосрочным финансовым операциям
| |
| Из Формулы (2.1.2) выводится формула доходности краткосрочных финансовых операций в виде ставки простых процентов:
| |
|  ,т.е. ,т.е.
| |
|  , ,
| (2.1.3)
| |
| где  время между покупкой и продажей актива в днях (месяцах); время между покупкой и продажей актива в днях (месяцах);
 количество дней в году (месяцах); количество дней в году (месяцах);
 цена покупки актива; цена покупки актива;
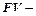 цена продажи актива.
Именно так вычисляется показатель реальной доходности инвестиции со сроком погашения до года. цена продажи актива.
Именно так вычисляется показатель реальной доходности инвестиции со сроком погашения до года.
| |
| Пример 2.1.2.Корпоративные облигации номиналом 10 тыс. д.е. со сроком обращения 6 месяцев продаются в день выпуска по цене 8 тыс. д.е., а через 30 дней – по цене 8,2 тыс. д. е. Определить:
1) Доходность облигаций к погашению;
2) Доходность при досрочной продаже в виде ставки простых процентов (рассматриваемые облигации относятся к ряду таких ценных бумаг, операции с которыми до срока погашения осуществляются ниже номинала).
| |
| 
| 
| |
| Ответ: доходность облигации к погашению составляет 50%, а доходность при досрочной продаже через 30 дней 30%.
| |
| Найти ставку доходности по краткосрочным финансовым операциям возможно и в том случае, если задан курс ценной бумаги, т.е.
 .
Для этого преобразуем Формулу (2.1.3) следующим образом: .
Для этого преобразуем Формулу (2.1.3) следующим образом:
 , т.е. , т.е.
| |
| 
| (2.1.4)
| |
| Пример 1.10.2Курс дисконтной облигации со сроком обращения 91 день в день выпуска –75% от номинала. Оценить доходность к погашению.
| |
| 
| 
| |
| Ответ: 131% годовых.
| |
| Формула простых процентов с плавающей ставкой
| | Плавающий процент- это изменяющаяся ставка в течении срока вклада или кредита.
| В условиях нестабильной экономической конъюнктуры процентные ставки часто меняются. В этом случае общая сумма долга вычисляется по формуле простых процентов с плавающей ставкой:
|  , ,
| (2.1.5)
| | Плавающие проценты – реальность нашей жизни.
| где  - количество дней в году; - количество дней в году;
 цена покупки актива; цена покупки актива;
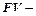 цена продажи актива. цена продажи актива.
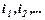 – последовательные значения ставок; – последовательные значения ставок;
 – число дней, в течение которых действуют соответствующие ставки. – число дней, в течение которых действуют соответствующие ставки.
| | Пример 1.1.2. Определите сумму на счете по состоянию на 1 апреля, если вклад сделан 1 января в размере 400 тыс. руб., процентная ставка равнялась 24 % годовых, но с 31 января введена новая ставка–36%. Капитализация процента ежеквартальная.
| |
| 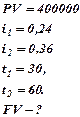
| 
| |
| Ответ: сумму на счете к 1 апреля составит 432000 руб.
| |
| Банки дают кредиты на разных условиях: и суммы разные, и процент не один и тот же, и сроки кредитов, естественно неодинаковы. Каков средний процент?
| | Средний процент –неизменная ставка процента, которая даёт то же результат финансового инструмента, что и плавающий процент.
| Выведем формулу среднего процента при использовании простых процентов: 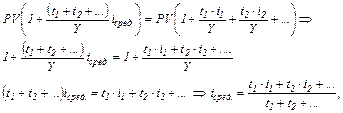
| |
| Таким образом,
|
| |
| 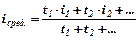
| (2.1.6)
| |
| Средний процент носит в основном справочный характер.
| | | | | | | | | | | | | | | |
|
| 2.1.4. Наращение по сложной процентной ставке
| | Сложный процент – это «процент на процент»
|
Вопрос вычисления сложных процентов является ключевым в финансовой математике.
Так как процент, выплачиваемый по ссуде или вложенному капиталу, присоединяется к основной сумме, в результате чего проценты выплачиваются и на основную сумму, и на полученные проценты. Проиллюстрируем это на примере.
Пример вычисления сложных процентов
Исходная сумма 1000 руб., процентная ставка –10% годовых
| | Сложные проценты (Compound interest) – проценты, получаемые на инвестируемые проценты.
| Срок
| Исходная стоимость
| Проценты по основной сумме, начисленные за исходный срок
| Проценты на процент
| Конечная стоимость
| |
|
| 
| 
|
| |
|
| 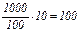
| 
|
| |
|
|
| 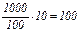
| 
|
| |
|
|
| 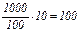
| 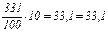
| 1463,1
| |
|
Итак, при наращении по сложной процентной ставке  за период – каждая следующая сумма больше предыдущей на долю за период – каждая следующая сумма больше предыдущей на долю  от предыдущей суммы.
Пусть исходная (современная) стоимость денег PV. Наращенную (будущую) сумму денег через от предыдущей суммы.
Пусть исходная (современная) стоимость денег PV. Наращенную (будущую) сумму денег через  периодов обозначим периодов обозначим  . Тогда, . Тогда,
| к концу 1- периода:
| 
| | к концу 2- периода::
| 
| | к концу 3- периода::
| 
| | …………………..
| ………………………………………………….
| | к концу n- периода:
| 
| Последовательность наращенных сумм:  есть геометрическая прогрессия с начальным членом есть геометрическая прогрессия с начальным членом  и знаменателем прогрессии и знаменателем прогрессии 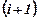 . .
Таким образом, получили формулу для вычисления наращенной сумму денег по сложной процентной ставке:
| |
|  , ,
| (2.2.1)
| |
| где 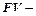 сумма долга (вклада) с процентами; сумма долга (вклада) с процентами;
 номинальная сумма кредита (вклада); номинальная сумма кредита (вклада);
 число периодов (лет); число периодов (лет);
 процентная ставка за период. процентная ставка за период.
| | Прогадал ли индейский вождь?
| Пример.Остров Манхэттен был «куплен» в 1624 г. у индейского вождя за 24 $. Стоимость земли этого острова 350 лет спустя оценивалась в 40 млрд. $. Прогадал ли индейский вождь, еслисредний процент по долгосрочным займам в XX веке в США составлял 6,3%?
| |
| 
| 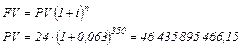
| |
| Для облегчения расчетов сложных процентов составлены таблицы мультиплицирующих множителей наращения.
Коэффициент наращения показывает, во сколько раз возрастает за  периодов сумма, положенная в банк под периодов сумма, положенная в банк под  процентов: процентов:
 Величина
Величина  есть будущая стоимость одной денежной единицы через есть будущая стоимость одной денежной единицы через  периодов при ставке процента периодов при ставке процента  . Таблицы таких множителей приведены в Приложении 2. . Таблицы таких множителей приведены в Приложении 2.
| |
| Пример Какой величины достигнет долг, равный 100 тыс. д.е., через 2 года при 12% годовых по сложной ставке.
| |
| 
| 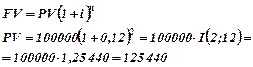
| |
|
При работе со сложными процентами иногда для приближенного оценивания полезно знать следующие правила.
| |
| Формулу (1.4.1) используют и в том случае, когда срок для начисления процентов являются дробным числом.
| |
|
| |
| 2.4. Исчисление процентной ставки, срока платежа и процентов за весь срок
| |
| Из Формулы (2.1.2) выводится формула доходности финансовых операции в виде ставки сложных процентов:
|  
| (2.2.2)
| |
| ПримерФинансовый инструмент размещается на срок 2 года по цене 1 000 000 д.е., а погашается по цене 1 200 000 д.е. Вычислить доходность в виде ставки сложных процентов.
| 
| 
| |
| Ответ: доходность финансового инструмента составит 9,54%.
| | RCY
–«реально накопленная доходность инвестиций»
англ.–realized compound yield
| Именно так вычисляется показатель реальной доходности инвестиции RCY. В этом случае в Формуле (2.2.2) в числителе дроби стоит наращённая сумма всех инвестиций и реинвестированных доходов от них, а в знаменателе – первоначальные вложения. Их соотношение показывает относительный рост за весь срок « » инвестиций, а извлечение корня степени « » инвестиций, а извлечение корня степени « » и вычитание 1 даёт годовые проценты. » и вычитание 1 даёт годовые проценты.
| |
| Проценты за весь срок вычисляются по формуле:
| |
| Сумма процентов за  периодов по сложной процентной ставке вычисляется по формуле: периодов по сложной процентной ставке вычисляется по формуле:
| |
| 
| (2.2.3)
| | Пример Ссуда была выдана на два года — с 1 мая 2006 года по 1 мая 2008 года. Размер ссуды — 10 000 руб. Необходимо распределить начисленные проценты (ставка 14 % АСТ/АСТ) по календарным годам.
| |
| 
|  1 способ:
1) за период с 1 мая до конца 2006 года (244 дня):
1 способ:
1) за период с 1 мая до конца 2006 года (244 дня):
 2) За 2007 год:
2) За 2007 год:
 3) c 1 января до 1 мая 2008 года (121 день):
3) c 1 января до 1 мая 2008 года (121 день):
 2 способ:
2 способ:

| |
| Методы ФЭР позволяют определять необходимый срок окончания или начала финансовой операции и её протяженность, если заданы  . Для этого формула (2.2.4) решаются относительно . Для этого формула (2.2.4) решаются относительно  : :
| 
| (2.2.4)
| |
| К удвоению ваших сбережений за определённый промежуток времени могут быть применены некоторые эмпирические правила. Одно из которых–«правило семидесяти двух»
| |
| Правило 72. Если процентная ставка есть  , то удвоение капитала по такой ставке происходит примерно за , то удвоение капитала по такой ставке происходит примерно за  лет. лет.
| |
| Это правило применяется для небольших ставок.
Пример Через сколько лет произойдёт удвоение капитала при ставке сложных процентов  .Сравнить результаты точного вычисления и вычисления по «правилу 72». .Сравнить результаты точного вычисления и вычисления по «правилу 72».
| |
| 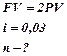
| 1. точное вычисление:

 года. года.
| |
| 2.3. Формула сложных процентов с плавающей ставкой
| |
| Формула (1.4.1) предполагает постоянную ставку на протяжении всего срока начисления процентов. В случае, когда изменение размеров ставок фиксируется в контракте, то формула сложных процентов с плавающей ставкойимеет вид:
| |
|  , ,
| (2.2.5)
| |
| где 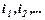 – последовательные значения ставок; – последовательные значения ставок;
 – периоды, в течение которых действуют соответствующие ставки.
Пример У вас есть 10 000 рублей. Сейчас на рынке продаются и покупаются акции фирмы «АБВ» и фирмы «ЭЮЯ» по 1000 рублей каждая. Фирма «АБВ» обещает 10% годового дохода в первый год и 20% - во второй. Фирма «ЭЮЯ» - 15 и 10 соответственно. Какой максимальный дохода за 2 года вы можете получить, купив акции этих компаний? – периоды, в течение которых действуют соответствующие ставки.
Пример У вас есть 10 000 рублей. Сейчас на рынке продаются и покупаются акции фирмы «АБВ» и фирмы «ЭЮЯ» по 1000 рублей каждая. Фирма «АБВ» обещает 10% годового дохода в первый год и 20% - во второй. Фирма «ЭЮЯ» - 15 и 10 соответственно. Какой максимальный дохода за 2 года вы можете получить, купив акции этих компаний?
| |
| 
| Очевидно что максимальный доход будет достигнут если в первый год будут куплены акции«ЭЮЯ»,а во второй «АБВ». Воспользуемся формулой сложных процентов с плавающей ставкой 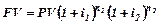
 года. года.
| |
| Соответственно доход составит 3800.
| |
| СРЕДНЯЯ ПРОЦЕНТНАЯ СТАВКА
| | Средний процент –неизменная ставка процента, которая даёт то же результат финансового инструмента, что и плавающий процент.
|  Пример. Вычислите средний процент с 1 июля 1998 г. по 30 июня 2000 г., если капитализация процента совершалась раз в квартал, а процент годовых изменился два раза: с 25% до 21% 1 апреля 1999 г. и 1 января 2000 г. ставка процента уменьшилась на 5 процентных пунктов.Ответ: 21,2%
Пример. Вычислите средний процент с 1 июля 1998 г. по 30 июня 2000 г., если капитализация процента совершалась раз в квартал, а процент годовых изменился два раза: с 25% до 21% 1 апреля 1999 г. и 1 января 2000 г. ставка процента уменьшилась на 5 процентных пунктов.Ответ: 21,2%
| |
|
|
| |
|
| |
| Начисление процентов более одного раза в год. Номинальная я процентная ставка наращения. Непрерывное наращение процентов
| | Сложный процент- это естественно!
| Часто в финансовых операциях в качестве периода наращения процентов используется не год, а, например, месяц, квартал или другой период. В этом случае если годовая (номинальная) ставка равна  , то проценты за один период начисляются по ставке , то проценты за один период начисляются по ставке  , а количество начислений за , а количество начислений за  лет будет равно лет будет равно  . Общая формула для расчета . Общая формула для расчета  по истечении по истечении  лет, при использовании годовой (номинальной) процентной ставки наращения лет, при использовании годовой (номинальной) процентной ставки наращения  , если проценты начисляются , если проценты начисляются  раз в год, будет иметь вид: раз в год, будет иметь вид:
| |
| 
| (2.2.6)
| |
| Исследуем зависимость между  и частотой начисления процента, т.е. и частотой начисления процента, т.е.  . Для этого рассмотрим пример.
Пример 1.2.1.Как изменится величина вклада в размере 1000 рублей при 200% годовых в зависимости от периода капитализации
Решение. . Для этого рассмотрим пример.
Пример 1.2.1.Как изменится величина вклада в размере 1000 рублей при 200% годовых в зависимости от периода капитализации
Решение.
| | Количество капитализаций за год
| Величина вклада
| С капитализацией раз год, т. е. 
| 
| С капитализацией раз в полгода, т. е. 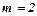
| 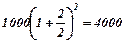
| С капитализацией раз в квартал, т. е. 
| 
| С ежедневной капитализацией, т. е. 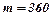
| 
| | Период капитализациипроцента – срок, в конце которого начисляется процент и сумма процента прибавляется к вкладу (причисленный процент).
| Таким образом, при непрерывном начислении процентов доход на вложенный капитал составит почти 738%-100%=638% годовых.
Вывод очевиден, чем чаще начисляются проценты, тем больше  в конце года, при этом, по мере сокращения интервалов начисления, темпы роста в конце года, при этом, по мере сокращения интервалов начисления, темпы роста  снижаются. Пределом является снижаются. Пределом является  при непрерывном начислении, т.е. ежедневное начисление процентов. Величина при непрерывном начислении, т.е. ежедневное начисление процентов. Величина  при непрерывном начислении приближённо, с хорошей степенью точности, вычисляется с помощью второго замечательного предела. Дело в том, что при непрерывном начислении приближённо, с хорошей степенью точности, вычисляется с помощью второго замечательного предела. Дело в том, что
 Тогда при
Тогда при  Формула (2.2.6)преобразуется: Формула (2.2.6)преобразуется:  Итак, формула для расчета
Итак, формула для расчета  по истечении по истечении  лет, при использовании годовой (номинальной) процентной ставки наращения лет, при использовании годовой (номинальной) процентной ставки наращения  , если проценты начисляются непрерывно, будет иметь вид: , если проценты начисляются непрерывно, будет иметь вид:
| 
| (2.2.6)
| |
Сложный процент восстанавливает справедливость. Переоформление вкладов ничего не приносит банкиру, кроме хлопот. Во избежание процедуры изъятия и повторного вклада обе стороны кредитной и депозитной сделки заранее договорились об использовании сложных процентов.
Чаще всего проценты начисляются раз в год, но в условиях высокой инфляции рассматриваются и другие временные сроки.
В кредитных договорах и банковских правилах это звучит примерно так:
«Ежеквартально сумма вклада увеличивается на.. процентов» или
«Проценты по вкладу капитализируются каждые три месяца», или
«Сумма процентов по вкладу прибавляется к основному вкладу раз в три месяца».
| |
| ЭФФЕКТИВНАЯ ПРОЦЕНТНАЯ СТАВКА
| | ARP-
англ. Annual Percentage Rate
эффективная ставка процента
| В качестве эталона «финансового метра» используется эффективная ставка процента (термин принятый в США, Европе и России) или, что то же самое, ARP–годовая ставка процента.
Эффективная ставка ARP – это годовая ставка сложных процентов, которая даёт тот же результат, что и  разовое начисление процентов по ставке разовое начисление процентов по ставке  , т.е. , т.е.
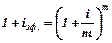 .
Решив данное уравнение относительно .
Решив данное уравнение относительно  и и  , получим: , получим:
| | «ГОДОВАЯ СТАВКА ПРОЦЕНТА
(ARP) –
есть мера действительной стоимости кредита»
из руководства МВА
| 
| (2.2.7)
| 
| (2.2.8)
| Эффективная ставка при  больше номинальной.
Обе ставки эквивалентны в финансовом отношении, т.е. замена в договоре номинальной ставки больше номинальной.
Обе ставки эквивалентны в финансовом отношении, т.е. замена в договоре номинальной ставки  при при  разовом начислении процентов на эффективную ставку разовом начислении процентов на эффективную ставку  не изменит финансовых обязательств участников сторон. не изменит финансовых обязательств участников сторон.
| | 3.
| Сравнение силы роста простых и сложных процентов
| |
| При одной и той же ставке  наращение сложных процентовидет быстрее, чем простых процентов, при длине периода наращения более единичного, и медленнее, если период наращения менее единичного.
Пример. Пусть сумма в 1000 ден. ед. наращивается по ставке 10% простых и сложных процентов. Тогда наращенные суммы таковы: наращение сложных процентовидет быстрее, чем простых процентов, при длине периода наращения более единичного, и медленнее, если период наращения менее единичного.
Пример. Пусть сумма в 1000 ден. ед. наращивается по ставке 10% простых и сложных процентов. Тогда наращенные суммы таковы:
| при   ,
при ,
при   . .
| промежутки
| I кв.
| II кв.
| III кв.
| IV кв.
| 2 год
| 3 год
| 4 год
| 5 год
| | Простые проценты
|
|
|
|
|
|
|
|
| | Сложные проценты
|
| 1048,8
| 1074,1
|
|
|
| 1464,1
| 1610,5
| | Сложный процент даёт рост «вклада» в геометрической прогрессии, а простой процент – в арифметической. При больших сроках разница может быть впечатляющей.
| Графики функций  и и  , в зависимости от , в зависимости от  показаны на Рис. 1.2.
ВСТАВИТЬ РИСУНОК!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! показаны на Рис. 1.2.
ВСТАВИТЬ РИСУНОК!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
| |
|
| |
| 1.6. СМЕШАННАЯ ПРОЦЕНТНАЯ СТАВКА
| | Смешанный процент – это простой процент «внутри» года (или иного срока капитализации) и сложный процент по годам.
| Есть и иная форма сосуществования простого и сложного процентов – это смешанный процент. Смешанный процент начисляется при дробном числе лет (точнее периодов начисления процентов) по формуле:
| 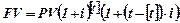 , ,
| (2.3.1)
| |
| где  – целое число лет, – целое число лет,
 – это оставшаяся доля последнего года. – это оставшаяся доля последнего года.
| |
| Пример.Найти во сколько увеличится сумма долга при сроке 2 года и 7 месяцев при 12% годовых.
| |
| 
| 
| |
| ПримерКредит на покупку квартиры в размере 1млн руб. выдан на 5 лет и 6 месяцев под 16,5% сложных годовых. Рассчитайте сумму долга обычным и смешанным методами.
| |
| 
| Сумма долга на конец срока обычным методом сложных процентов определяется:
 в свою очередь, смешанный метод даёт:
в свою очередь, смешанный метод даёт:

| | | | | | | | | | | | | | | | | | | | | | | | | | | | Эталонная эффективная ставка определяется для следующей стандартной схемы кредита: срок кредита год, весь кредит выдаётся в начале года, а погашается вместе с суммой процента в конце года. В этом случае номинальный процент и эффективная ставка процента совпадают?????
| Количество вариантов схем кредитов практически неограниченно. Как же их сравнить между собой?
Ответ очевиден: по доходности. Для этого важно научиться определять доходность некоторым стандартным способом. Этот способ получил название эффективной ставки процента.
Вычисление эффективной ставки является довольно непростой задачей.
ПримерСравнить доходность двух кредитов. Один даётся на 7 лет с условием выплаты 10% в конце каждого года в качестве платы за пользованием кредитом. Это стандартная схема множества долгосрочных кредитов. Другой кредит относится к потребительскому кредитованию, проще говоря, к покупке в рассрочку. Условия покупки таковы: при получении товара оплачивается 40% его стоимости, а через год вносится оставшаяся часть и 10% от стоимости товара в качестве платы за кредит. Доходность какого из вариантов кредита выше для кредитора?
1 вариант 10% годовых
2 вариант  годовых.
Таким образом, одно и то же число, фигурирующее в различных кредитных договорах в качестве процента, часто означает разные действительные цены кредита.
20% годовых вперёдэто совсем не то, что20% послепользования кредитом.
Действительно, при уплате 20% вперёд заёмщик получает на руки 80% кредита и возвращает 100% через год, т.е. платит годовых.
Таким образом, одно и то же число, фигурирующее в различных кредитных договорах в качестве процента, часто означает разные действительные цены кредита.
20% годовых вперёдэто совсем не то, что20% послепользования кредитом.
Действительно, при уплате 20% вперёд заёмщик получает на руки 80% кредита и возвращает 100% через год, т.е. платит  годовых.
В жизни и крупные кредиты и мелкие займы часто получаются, и возвращаются не сразу, а тоже частями, поэтому не зная основ финансовой математики, люди плохо ориентируются в этих своеобразных ценах рынка ссудного капитала.
Важность общего стандарта цен кредитов сложно переоценить. Ведь заёмщиками в рыночной экономике выступают все: владельцы кредитных карт, покупатели в рассрочку, фирмы, государство.
В США даже принят закон – Закон о защите потребительского кредита, который требует информировать заёмщиков об истинной цене кредита, т.е. об эффективной ставке процента, а также о номинальном превышении суммы, уплачиваемой в рассрочку, над ценой приобретаемого товара. Это позволяет защищать граждан от финансовых жуликов, делая понятными «ценники в финансовом мире».
Как вычислять эффективную ставку процента:
1 ) Для кредита с разовым кредитованием и разовым возвратом суммы кредита плюс суммы процента
Пусть годовых.
В жизни и крупные кредиты и мелкие займы часто получаются, и возвращаются не сразу, а тоже частями, поэтому не зная основ финансовой математики, люди плохо ориентируются в этих своеобразных ценах рынка ссудного капитала.
Важность общего стандарта цен кредитов сложно переоценить. Ведь заёмщиками в рыночной экономике выступают все: владельцы кредитных карт, покупатели в рассрочку, фирмы, государство.
В США даже принят закон – Закон о защите потребительского кредита, который требует информировать заёмщиков об истинной цене кредита, т.е. об эффективной ставке процента, а также о номинальном превышении суммы, уплачиваемой в рассрочку, над ценой приобретаемого товара. Это позволяет защищать граждан от финансовых жуликов, делая понятными «ценники в финансовом мире».
Как вычислять эффективную ставку процента:
1 ) Для кредита с разовым кредитованием и разовым возвратом суммы кредита плюс суммы процента
Пусть  сумма кредита, а за сумма кредита, а за 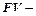 сумма к возврату через время сумма к возврату через время  . Тогда . Тогда  , где , где  .
При этом не важно, меньше или больше года величина .
При этом не важно, меньше или больше года величина  , важно, чтобы время было выражено в годах.
ПримерДопустим на 3 месяца дан кредит под 40% годовых. Соответственно по банковскому обыкновению (на по формуле простых процентов), за три месяца будет начислено 10% годовых. , важно, чтобы время было выражено в годах.
ПримерДопустим на 3 месяца дан кредит под 40% годовых. Соответственно по банковскому обыкновению (на по формуле простых процентов), за три месяца будет начислено 10% годовых.
| | Теперь выясним, какая из форм расчётов (процентов) наиболее выгодна для вкладчика (кредитора) и заёмщика. Для этого произведём вычисления будущей стоимости денег различными рассмотренными выше способами, сравним их и сделаем выводы.
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|
Типы конфликтных личностей (Дж. Скотт) Дж. Г. Скотт опирается на типологию Р. М. Брансом, но дополняет её. Они убеждены в своей абсолютной правоте и хотят, чтобы...
Гносеологический оптимизм, скептицизм, агностицизм.разновидности агностицизма Позицию Агностицизм защищает и критический реализм. Один из главных представителей этого направления...
Функциональные обязанности медсестры отделения реанимации · Медсестра отделения реанимации обязана осуществлять лечебно-профилактический и гигиенический уход за пациентами...
|
РЕВМАТИЧЕСКИЕ БОЛЕЗНИ Ревматические болезни(или диффузные болезни соединительно ткани(ДБСТ))— это группа заболеваний, характеризующихся первичным системным поражением соединительной ткани в связи с нарушением иммунного гомеостаза...
Решение Постоянные издержки (FC) не зависят от изменения объёма производства, существуют постоянно...
ТРАНСПОРТНАЯ ИММОБИЛИЗАЦИЯ
Под транспортной иммобилизацией понимают мероприятия, направленные на обеспечение покоя в поврежденном участке тела и близлежащих к нему суставах на период перевозки пострадавшего в лечебное учреждение...
|
|