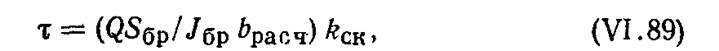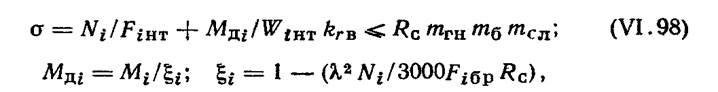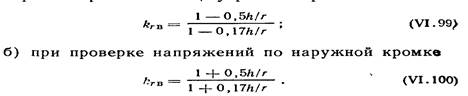Распорная система треугольного очертания
Распорную систему треугольного очертания проектируют с применением прямолинейных клеедощатых элементов, со стальной затяжкой или с опиранием непосредственно на фундаменты. Узлы в этой конструкции решают с эксцентриситетом (см. рис.VI.26),благодаря чему уменьшается расчетный изгибающий момент, который будет При равномерно распределенной нагрузке
К недостаткам эксцентричного решения узлов относится концентрация скалывающих напряжений в зоне опирания, что учитывается введением коэффициента
Рамы Рамные конструкции отличаются от арочных своим очертанием, которое сильно влияет на распределение изгибающих моментов в пролете. При ломаном очертании рамы в жестком карнизном узле при загружении как левой, так и правой половины рамы возникают моменты одного знака. В результате при загружении рамы по всему пролету угловые моменты сильно увеличиваются, что ограничивает длину пролетов, перекрываемых рамами, до 18—30 м. Рамы могут воспринимать горизонтальные нагрузки, обеспечивая поперечную устойчивость здания без защемления стоек и без устройства жестких поперечных стен. Рекомендуется делать рамы трехшарнирными, так как в статически определимых системах не происходит перераспределения усилий при деформировании под длительно действующей нагрузкой, что обеспечивает Соответствие их расчетным усилиям. Дощатоклееные гнутые рамы. Дощатоклееные гнутые рамы (рис. VI.30) выполняют трехшарнирными, что облегчает их изготовление, транспортирование и монтаж. Криволинейность карнизных узлов достигается выгибом слоев (досок) по окружности при изготовлении рам. Радиус кривизны обычно невелик и составляет 2—4 м. Так как по условиям гнутья отношение радиуса кривизны к толщине слоя (R/8) не может быть меньше 150, то толщина слоев для изготовления дощатоклееных гнутых рам после фрезерования будет составлять не более 1,6— 2,5 см. Следовательно, дощатоклееные гнутые рамы более трудоемки в изготовлении, чем арки и требуют большего расхода древесины и клея. Кроме того, расчетное сопротивление изгибу уменьшается умножением на коэффициент гнутья, меньший единицы. Сечение рамы делают прямоугольным, а высоту сечения — переменной по длине, что достигается уменьшением числа досок в пакете с внутренней стороны рамы. Постепенное плавное изменение высоты сечения (рис. VI.30, а) предпочтительнее с архитектурной точки зрения, но технологически менее выгодно. Менее сложно и трудоемко изготовление дощатоклееных гнутых рам с применением ступенчатого изменения высоты сечения (рис, VI.30,б), которые разработаны для пролетов 12и 18 м (рис. VI.31). Рамы работают на сжатие и поперечный изгиб. В связи с переменностью высоты сечения нормальные напряжения следует проверять в различных местах рамы по длине. Нормальные напряжения находят по формулам для сжато-изгибаемого стержня:
где N,, Mi — нормальная сила и изгибающий момент в рассматриваемом сечении; F,6P и №1НТ — площадь и момент сопротивления рамы в рассматриваемом сечении; К — гибкость рамы, постоянная для всех сечений рамы; krB — коэффициент к расчетному сопротивлению, учитывающий криволинейносгь эпюры напряжений (рис. VI 32).
Коэффициент krB определяют по формулам: а) при проверке напряжений по внутренней кромке
|

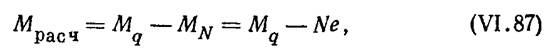 где Mq — момент от поперечной нагрузки; MN — разгружающий момент от продольной силы; е — эксцентриситет.
где Mq — момент от поперечной нагрузки; MN — разгружающий момент от продольной силы; е — эксцентриситет. Клееный элемент проверяют на прочность и устойчивость плоской формы деформирования по обычным формулам расчета сжато-изгибаемых элементов.
Клееный элемент проверяют на прочность и устойчивость плоской формы деформирования по обычным формулам расчета сжато-изгибаемых элементов.