Задача №3.
Дано: m = 0,3 кг
V0 = 4 м/с
Найти: VB, VC, VD, Nc.
Рассмотрим участок BC и применим для него теорему об изменении кинетической энергии (Изменение кинетической энергии системы равно сумме работ всех сил, действующих на систему)
Следовательно,
Для нахождения F̅ + R̅ + φ̅ = 0 Сила инерции по модулю равна массе тела, умноженной на её ускорение, а по знаку – противоположна. φ̅ = - mw̅ Также, она состоит из касательной и центробежной составляющих. φ̅ = φ̅n +φ̅τ |φ̅τ| =
Рассмотрим участок BC и применим для него теорему об изменении кинетической энергии (Изменение кинетической энергии системы равно сумме работ всех сил, действующих на систему):
Запишем теорему об изменении импульса (Разность импульсов в конечной и начальной точках движения равна сумме всех сил, действующих на точку, умноженную на время прохождения точкой этого участка): mV̅D – mV̅B = Рассмотрим участок BD и применим для него теорему об изменении импульса:
Из этого уравнения мы находим Vd
Этап №3. Определение скоростей точек системы с помощью теоремы об изменении кинетической энергии механической системы. Дано:
Эта задача на данном этапе решается с помощью теоремы об изменении кинетической энергии механической системы (Разность начальной и конечной кинетической энергии системы равна сумме работ внешних сил). Для применения этой теоремы необходимо будет найти суммарную кинетическую энергию системы в начальном и конечном положении. Т.к. в начальном положении система находилась в покое, то кинетическая энергия в этот момент равна нулю. Найдем значение кинетической энергии системы в конечном положении, она равна сумме кинетических энергий всех тел системы: T = T1 + T2 + T3 + T4 + T5 = Исходя из схемы системы, выразим все неизвестные в этом выражении через скорость первого тела: V1 = VA1 = ω2R2, откуда ω2 = VA2 = ω2r2 = ω3R3, откуда ω3 = VB2 = ω3r3 = Момент инерции тел 2,3,4 вычисляется по формуле: Iz = Iz4 =
Если теперь подставить всё это в формулу кинетической энергии и вынести за скобку Mпр = m1 +
Рисунок 2. Силы и реакции опор в системе.
Для составления правой части уравнения теоремы об изменении кинетической энергии, потребуется найти сумму работ всех внешних сил. Выпишем все внешние силы, действующие на систему и работы, которые они совершают: 1) Работа силы тяжести первого тела: A(G1) = m1gS1=4116 2) Работа момента сопротивления второго тела: A(Mc2) = -Mc2ϕ2= 3) Работа момента сопротивления третьего тела: A(Mc3) = -Mc3ϕ3 = 4) Работа силы тяжести четвертого тела: A(G4) =
Связи между перемещениями находим из связей между скоростями: ϕ2 =
Сумма работ всех внешних сил:
Fпр. = 2508,12 Запишем теорему об изменении импульса:
Этап №4. Исследование поступательного, вращательного и плоскопараллельного движений тел при помощи дифференциальных уравнений движения.
Найти: W1, ε2, ε3, ε4, W4, Т23,T34, T45, T40, I4 =?
2) Мысленно разрежем тела друг от друга для получения внешних сил из внутренних. Рассмотрим каждое тело в отдельности: (1) тело:
Укажем все силы, действующие на тело. Составим уравнения. m1W1 = m1g – Т12 200W1 = 200 ˑ 9,8 – Т12 (1) (2) тело:
Укажем все силы, действующие на тело. Составим уравнения: Т21 = - Т12
(3)
Укажем все силы, действующие на тело. Составим уравнения: J3ε3 = - Mc3 - T34r3 + Т32R3 J3 = m3i32 m3i32ε3 = - Mc3 - T34r3 + Т32R3 3,39ε3 = -100 – 0,25T34 – 0,28Т23
(3)
(4) тело:
Укажем все силы, действующие на тело. Составим уравнения: m4W4 = Т45 - T43 - T40 (4)
5
Составим уравнение m5W5 = m5g – Т54 m5W5 = m5g +Т45
Составим уравнения кинематических связей: V1 = ω2R2 W1 = ε2R2 (6) ω2r2 = ω3R3 ε2r2 = ε3R3 (7) ω3r3 = ω42R4 ε3r3 = ε4R4 + r4 (8) Vc2 = ω4R4 W4 = ε4R4 (9)
200W1 = 200 ˑ 9,8 – Т12 (1)
50W4 = Т45 + 50 ˑ 9,8 - T43 - T40 (4) 3,125 ε4 = (50 ˑ 9,8 + T45) ˑ 0,11 – T43 ˑ 0,22 (5) 100W4 = 980 +Т45 (6) W1 = 0,24ε2 (7) 0,19ε2 = 0,28ε3 (8) W4 = 0,11ε4 (10)
Имеем систему из 9 уравнений с 9 неизвестными. Подставляем в (6) уравнение значение W1 = 6,67 м/с (взятое из 5 этапа): ε2 = 27,5 рад/с2 Дальше по цепочке подставляем полученные значения. Из (7): ε3 = 18,7 рад/с2 Из (8): ε4 = 18,7 рад/с2 Из (9): W4 = 2,05 м/с2 Из (1): Т12 = 640 H Из (2): Т32 = 1001,89 H Из (2): Т43 = 514,38 H Из (2): Т45 = 1070 H Из (2): Т40 = 943,12 H
Этап №5. Применение уравнений Лагранжа второго рода к механическим системам с одной степенью свободы. Дано:
Дифференциальное уравнение Лагранжа:
Где Qj – обобщенная сила S – число степеней свободы j = 1,2….S qj – обобщенная координата
Применительно к нашей задаче: S = 1 q = x
Сумма кинетических энергий всех тел будет записана как: T = Уравнение Лагранжа для нашей задачи:
Проделаем следующие операции:
Для определения обобщенной силы, соответствующую обобщенной координаты необходимо записать выражение для элементарной работы всех активных сил на возможные перемещения точек системы. В этом выражении вынести за скобку возможных перемещений обобщенные координаты, и тогда выражение в скобках будет называться обобщенной силой. Проделаем следующие операции:
Для определения обобщенной силы, соответствующей обобщенной координате, необходимо записать выражение для элементарной работы всех активных сил на возможные перемещения точек системы. В этом выражении вынести за скобку возможных перемещений обобщенные координаты, и тогда выражение в скобках будет называться обобщенной силой.
Связь между перемещениями берем из связи между скоростями:
Подставим это в формулу (1):
откуда W1 = Ответ: W1 = 6,67 м/с2.
|

 0,2 c
0,2 c xx
xx

 – сумма работ внешних сил, где h – высота подъема шарика, а Fтр – сила трения.
– сумма работ внешних сил, где h – высота подъема шарика, а Fтр – сила трения.


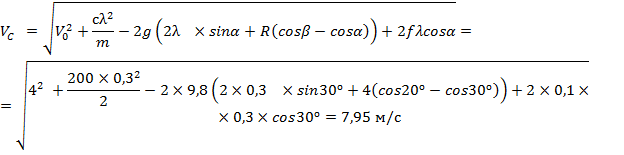
 применим принцип Даламбера (В любой момент времени векторная сумма всех активных сил, всех реакций связей и мысленно приложенной силы инерции равна нулю):
применим принцип Даламбера (В любой момент времени векторная сумма всех активных сил, всех реакций связей и мысленно приложенной силы инерции равна нулю): |φn| =
|φn| =  , где ρ = R = 4.
, где ρ = R = 4.

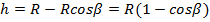
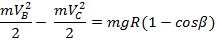
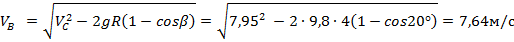





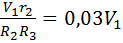
 , откуда ω4 =
, откуда ω4 = 

 =3
=3 , то всё, что останется в скобке, обозначим за приведенную массу. В итоге получим:
, то всё, что останется в скобке, обозначим за приведенную массу. В итоге получим:

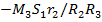
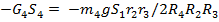



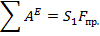

 ,откуда
,откуда 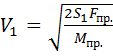 =
=  = 5,3 м/с.
= 5,3 м/с.

 ˑ ε4 = (50 ˑ 9,8 + T45) ˑ R4 – T43 ˑ 2R4
ˑ ε4 = (50 ˑ 9,8 + T45) ˑ R4 – T43 ˑ 2R4 (2)
(2)
 – обобщенная скорость
– обобщенная скорость

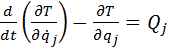 (1)
(1)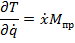

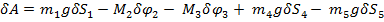

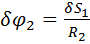



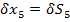
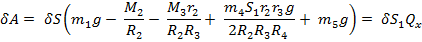
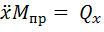
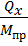 = 6,67 м/с2
= 6,67 м/с2


