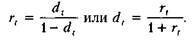Операции наращения и дисконтирования
Гидравлический расчет системы отопления сводится к определению диаметров всех трубопроводов, при которых, используя располагаемое давление, можно обеспечить затекание на каждый участок, в стояк и прибор необходимого количества теплоносителя. Вычертим схему систему отопления с установкой всей необходимой арматуры (вентелей, кранов и т.д.) и стояка с приборами расчетного циркуляционного кольца. Систему отопления разделим на участки с неизменным расходом теплоносителя и постоянным диаметром и прономеруем их. Расчет будем проводить по методу характеристик сопротивления. При этом расчет сводиться к суммированию гидравлических потерь на всех участках системы. Метод характеристик сопротивления определяет гидравлические потери (∆р, кг/м2) на участке трубопровода из соотношения: ∆р = Si * Gi2, (8.1) где Si – характеристика сопротивления участка трубопровода, (кг/м2)/(кг/ч)2, равная потери давления в нем при расходе теплоносителя 1 кг/ч. Определяется по формуле: Si = Sn.m. * li + ∑SMi, (8.2) где Sn.m. – удельная характеристика сопротивления, учитывающая потери давления на трение на 1 погонный метр трубопровода, (кг/м2)/(кг/ч)2; li – длина отдельного участка; ∑SMi – суммарная характеристика сопротивления, учитывающая все местные сопротивление на участке, (кг/м2)/(кг/ч)2; Gi – расход теплоносителя на участке; Gi = Qi / с * (tr – t0), (8.3) Расчет стояка производится, как одного участка, включающего в себя этажи стояка, узлы присоединения, подводящие и отводящие трубопроводы, арматуру. По условиям гидравлической устойчивости вертикального стояка однотрубных систем требуемые потери давления в стояке ∆рСТТР должны составлять 80-90 % от величины располагаемой разности давления ∆рр на входе в систему отопления (от элеватора): ∆рСТТР = (0,8 ÷0,9)* ∆рр, (8.4) Если величина ∆рСТ отличается от ∆рСТТР, необходимо изменить сопротивление стояка, увеличивая или уменьшая диаметр участков стояка. В расчете для зданий с числом этажей 3-5 принимаем: ∆рр = 800÷900 кг/м2. После расчета стояка приступаем к расчету магистральных трубопроводов. Определим полные потери давления: ∆р = ∆рМТ + ∆рСТ Расчет считается законченным, если выполняется условие: ∆р ≤∆рр Если это условие не выполняется, надо изменить ∆рМТ , изменяя диаметр трубопроводов на отдельных участках. Результаты гидравлического расчета сводятся в таблицу 8.
Таблица 8- Гидравлический расчет системы отопления
Т.к. ∆р = 1090кг/м2 ≈ ∆рр = 800÷1200, то можно считать, что гидравлический расчет системы отопления выполнен правильно. Список используемой литературы
1. СНиП 23-01-99 Строительная климатология и геофизика, М.,1999. 2. СНиП 23-02-2003 Тепловая защита, М., 2003. 3. СНиП 41-01-2003. Отопление, вентиляция и кондиционирование воздуха. М, 2003. 4. «Ограждающие конструкции и теплотехническое оборудование жилого здания». Методические указания к курсовой работе по дисциплине «Теплотехника, газоснабжение и вентиляция». Чебоксары – 1983 г.
Операции наращения и дисконтирования Переход к рыночной экономике, укрепление и стабилизация условий функционирования рыночных механизмов сопровождается появлением видов деятельности, имеющих для финансового менеджера предприятия принципиально новый характер. Иными словами, появились новые возможности в отношении и привлечения, и инвестирования финансовых ресурсов. Все эти возможности имеют одну общую черту, являющуюся по сути ключевой, — временная ценность задействованных в финансовой операции средств. Данный параметр можно рассматривать в двух аспектах. Первый аспект связан с обесценением денежной наличности с течением времени. Представим, что предприятие имеет временно свободные денежные средства в размере 5 млн руб., а инфляция составляет 20% в год (т. е. цены увеличиваются в 1,2 раза). Это означает, что уже в следующем году, если хранить деньги «в чулке», они уменьшатся по своей покупательной способности и составят в ценах текущего дня лишь 4,17 млн руб. Второй аспект связан с обращением капитала (денежных средств). Для понимания существа дела рассмотрим пример. Предприятие имеет возможность участвовать в некоторой деловой операции, которая принесет доход в размере 10 млн руб. по истечении 2 лет. Предлагается выбрать вариант получения доходов: либо по 5 млн руб. по истечении каждого года, либо единовременное получение всей суммы в конце периода. Даже на житейском уровне очевидно, что второй вариант получения доходов явно невыгоден по сравнению с первым. Это проистекает из того, что сумма, полученная в конце первого года, может быть вновь пущена в оборот и, таким образом, может принести дополнительные доходы. На первый взгляд, такой вывод очевиден и не требует каких-то специальных знаний, однако проблема выбора моментально усложнится, если немного изменить условие задачи; например, доходы таковы: в первый год — 4 млн руб., а во второй — 5 млн руб. В этом случае уже не очевидно, какой вариант предпочтительнее. Приведенный пример можно усложнять и дальше, вводя дополнительные условия (инфляция, стохастичность величины доходов, выплачиваемых единовременно и периодически, оказание дополнительных услуг и т. п.).
Даже эти простейшие примеры позволяют сделать очевидное предположение: скорее всего практически любая финансовая операция должна учитывать фактор времени, а потому обоснованное принятие решений по поводу привлечения финансовых ресурсов и их инвестирования с необходимостью должно базироваться на некоторых счетных алгоритмах и методах. Суть этих алгоритмов — учет временной стоимости денег и сравнение эффективности альтернативных вариантов операции через систему процентных ставок. Рассматриваемые в совокупности, они являются одним из основных элементов практически любой системы финансового менеджмента. Наиболее интенсивно финансовые расчеты применяются для оценки инвестиционных проектов, в операциях на рынке ценных бумаг, в ссудо-заемных операциях, в оценке бизнеса и др. Проблема «деньги—время» не нова, поэтому уже разработаны удобные модели и алгоритмы, позволяющие ориентироваться в истинной цене будущих доходов с позиции текущего момента. Коротко охарактеризуем их в теоретическом и практическом аспектах.
Логика построения основных алгоритмов проста и основана на следующей идее. Простейшим видом финансовой сделки является однократное предоставление в долг некоторой суммы PV с условием, что через некоторое время t будет возвращена большая сумма FV. Как известно, результативность подобной сделки может быть охарактеризована двояко: либо с помощью абсолютного показателя — прироста (FV — PV), либо путем расчета некоторого относительного показателя. Абсолютные показатели чаще всего не подходят для подобной оценки ввиду их несопоставимости в пространственно-временном аспекте. Поэтому пользуются специальным коэффициентом — ставкой. Этот показатель рассчитывается отношением приращения исходной суммы к базовой величине, в качестве которой, очевидно, можно взять либо PV, либо FV. Таким образом, ставка рассчитывается по одной из двух формул:
В финансовых вычислениях первый показатель имеет следующие названия: «процентная ставка», «процент», «рост», «ставка процента», «норма прибыли», «доходность», а второй — «учетная ставка», «дисконтная ставка», «дисконт».
Очевидно, что обе ставки взаимосвязаны, т. е, зная один показатель, можно рассчитать другой. Оба показателя могут выражаться либо в долях единицы, либо в процентах. Различие в этих формулах состоит в том, какая величина берется за базу сравнения: в формуле (6.1) — исходная сумма, в формуле (6.2) — возвращаемая сумма. Как же соотносятся между собой эти показатели? Очевидно, что rt > dt, а степень расхождения зависит от уровня процентных ставок, имеющих место в конкретный момент времени. Так, если rt = 8%, dt = 7,4%, т.е. расхождение сравнительно невелико; если г, = 80%, то dt = 44,4%, т. е. ставки существенно различаются по величине. В прогнозных расчетах, например, при оценке инвестиционных проектов, как правило, имеют дело с процентной ставкой, хотя обычно это не оговаривается. Объяснение этому может быть таким. Во-первых, анализ инвестиционных проектов, основанный на формализованных алгоритмах, может выполняться лишь в относительно стабильной экономике, когда уровни процентных ставок невелики и сравнительно предсказуемы — в том смысле, что их значения не могут измениться в несколько раз или на порядок, как это имело место в России в переходный период от централизованно планируемой экономики к рыночной экономике. Если вероятна значительная вариабельность процентных ставок, должны применяться другие методы анализа и принятия решений, основанные, главным образом, на неформализованных критериях. При разумных значениях ставок расхождения между процентной и дисконтной ставками, как мы видели, относительно невелики, и потому в прогнозных расчетах вполне может быть использована любая из них. Во-вторых, прогнозные расчеты не требуют повышенной точности, поскольку результатами таких расчетов являются ориентиры, а не точные оценки. Поэтому, исходя из логики подобных расчетов, предполагающих их многовариантность, а также использование вероятностных оценок и имитационных моделей, излишняя точность не требуется.
Следует обратить внимание читателя на следующее весьма важное обстоятельство. В формулах (6.1) и (6.2) пока не акцентируется внимание на продолжительности периода, однако из алгоритма расчета с очевидностью следует, что обе ставки являются функцией времени: чем длительнее период, тем существеннее должно быть различие между суммовыми величинами PV и FV, а потому с изменением продолжительности временного интервала, т. е. продолжительности финансовой операции, должна меняться и ставка. Поскольку финансовые операции могут длиться от нескольких дней до нескольких лет, необходимо всегда помнить следующее правило: процентная ставка в финансовой операции должна быть некоторым образом увязана с продолжительностью операции. Обычно это делается путем задания некоторого базисного интервала, к которому привязывается ставка (год, квартал, месяц, день). Чаше всего характеристика финансовой операции делается с помощью годовой процентной ставки.
Процесс, в котором заданы исходная сумма и ставка (процентная или учетная), в финансовых вычислениях называется наращением, искомая величина — наращенной суммой, а используемая в операции ставка — ставкой наращения. Процесс, в котором заданы ожидаемая в будущем к получению (возвращаемая) сумма и ставка, называется дисконтированием, искомая величина — дисконтированной суммой (иногда используется термин приведенная сумма), а используемая в операции ставка — ставкой дисконтирования. В первом случае речь идет о движении денежного потока от настоящего к будущему, во втором — о движении от будущего к настоящему (рис. 6.1).
Ставка (i) Рис. 6.1. Логика финансовых операций
Итак, в любой простейшей финансовой сделке, предполагающей учет фактора времени с помощью операций наращения и (или) дисконтирования, следующие три параметра являются ключевыми: (а) схема наращения (дисконтирования), (б) используемая ставка, (в) продолжительность базисного периода (т. е. выбранное дробление финансовой операции на базисные периоды): при этом две величины предполагаются заданными, а одна является искомой.
Экономический смысл финансовой операции, задаваемой формулой (6.1), состоит в определении величины той суммы, которой будет или желает располагать инвестор по окончании этой операции. Поскольку из формулы (6.1)
FV = PV + PV *rt (6.3)
и PV *rt > 0,
то видно, что время генерирует деньги.
Разность I = (FV - PV) называется процентом. Это величина дохода от предоставления в долг денежной суммы PV. (Заметим, что в математике процентом называют сотую долю некоторого числа, что, естественно, отличается от экономического понятия «процент».)
На практике доходность является величиной непостоянной, зависящей, главным образом, от степени риска, ассоциируемого с видом бизнеса, в который сделано инвестирование капитала. Связь здесь прямо пропорциональная: чем рискованнее бизнес, тем выше значение доходности. Считается, что наименее рисковы вложения в государственные ценные бумаги или в государственный банк, однако доходность операции в этом случае относительно невысока.
В еличина FV показывает как бы будущую стоимость «сегодняшней» величины PV при заданном уровне доходности.
Поскольку из формулы (6.2)
PV = FV -(1-dt) (6.4)
и (l-dt)< 1,
то опять приходим к выводу, что время генерирует деньги.
Экономический смысл дисконтирования заключается во временном упорядочении денежных потоков различных временных периодов. Одна из интерпретаций ставки, используемой для дисконтирования, такова: ставка показывает, какой ежегодный процент возврата хочет (или может) иметь инвестор на инвестируемый им капитал. В этом случае искомая величина PV показывает как бы текущую, «сего--дняшнюю» стоимость будущей величины FV.
Пример
Предприятие получило кредит на один год в размере 5 млн руб. с условием возврата 10 млн руб. В этом случае с помощью формул (6.1) и (6.2) несложно рассчитать, что процентная ставка равна 100%, а дисконт — 50%.
Итак, наращение и дисконтирование — две взаимообратные операции, согласующиеся логически и алгоритмически. Они обеспечивают сопоставимость величин PV и FV с учетом фактора времени и предполагаемой (или требуемой) нормы прибыли. Наращение позволяет получить оценку той суммы FV, на которую можно рассчитывать в будущем, инвестировав некоторым образом исходную сумму PV. Дисконтирование позволяет дать оценку ценности ожидаемой суммы с позиции более раннего момента времени и учета временной ценности денег. Если PV — дисконтированная величина ожидаемой к получению суммы FV, то наиболее наглядная интерпретация этих оценок такова: PV показывает, сколько инвестор готов заплатить «сегодня» за возможность получения суммы FV «завтра» (т.е. в будущем). В известном смысле PV и АV равны, т.е. инвестору безразлично, обладать ли суммой PV «сегодня» или суммой FV «завтра». PV — это осторожная оценка суммы FV. Связывающая величины PV и FV процентная ставка характеризует уровень эффективности соответствующей финансовой операции, заключающейся в том, что инвестор отказывается от PV «сегодня» в пользу FV «завтра», что автоматически предполагает за это долготерпение некоторое вознаграждение в виде превышения FV над PV. Чем выше ставка и чем большее число базисных периодов между моментами, в который ожидается получение FV и к которому эта величина дисконтируется, тем больше различие между PV и FV. Поскольку продолжительность финансовой операции обычно предопределена, т. е. известно, когда можно ожидать получение FV, осторожность в оценке FV, с позиции предшествующего момента времени, достигается за счет варьирования процентной ставкой, причем чем выше значение ставки, тем меньше значение PV, т. е. более осторожно оценивается ценность ожидаемой в будущем суммы FV.
Заканчивая раздел, уместно напомнить о том, что идея наращения и дисконтирования, в том числе в приложении к экономике, имеет давнюю историю. Таблицы сложных процентов были впервые разработаны и опубликованы математиками Я. Тренченом (Jan Trenchant) и С. Стевином (Simon Stevin, 1548— 1620) соответственно в 1558 и 1582 гг., причем именно Стевин высказал идею о возможности использования чистой дисконтированной стоимости для оценки финансовых инвестиций [The History of Accounting, p. 208]. Однако лишь в конце XIX в. эта идея получила активное развитие в работах экономистов. Так, в 1887 г. американский инженер А. Веллингтон (A. Wellington) опубликовал работу «Экономическая теория размещения железных дорог», в которой предложил подход к обоснованию целесообразности строительства новой дороги на основе сопоставления дисконтированных значений прогнозных притоков и оттоков денежных средств. В 1891 г. английский бухгалтер Ф. Mop (Francis More) впервые предложил оценивать гудвилл исходя из генерируемых им дополнительных доходов [Кат, р. 401—403]. Идея дисконтирования активно использовалась А. Маршаллом (Alfred Marshall, 1842—1924) и И, Фишером (Irving Fisher, 1867—1947) при изложении логики и техники бюджетирования капиталовложений и оценки инвестиционных альтернатив. На наращении и дисконтировании основаны алгоритмы решений на рынках ценных бумаг.
|

 (6.1)
(6.1) (6.2)
(6.2)