Ответ: 0.
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Решение: Решим систему матричным способом, для этого вычислим обратную матрицу
Решим систему методом Крамера. Главный определитель системы:
Запишем и вычислим вспомогательные определители
Ответ: Решим систему методом Гаусса, для этого составим расширенную матрицу системы и упростим ее приведением к треугольному виду.
Таким образом, система равносильна системе
Находим
Ответ: При решении всеми методами одной и той же системы, мы получим один ответ. Задача 3. Выполнить действия:
Решение. Выполним решение по действиям.
Ответ: Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы. Если Пример: Произведение Произведение
|
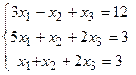
, где 
- алгебраические дополнения к элементам матрицы.
- матрица невырожденная.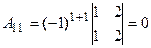
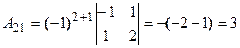
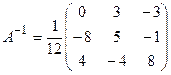
. Разложим определитель по элементам первой строки, пользуясь формулой 
.
Тогда 
~ 
~ 
~ 
, 
, 
=
.
.
.
, 
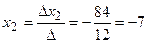
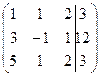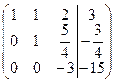
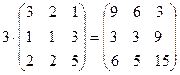, то произведением матрицы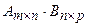 
называется матрица 
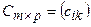, такая, что 
, где 
.
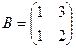
не определено, так как число столбцов матрицы А (3) не совпадает с числом строк матрицы В (2).
определено.
