МЕХАНИКА. определение моментов инерции параллелепипеда методом крутильных колебаний
ЛАБОРАТОРНАЯ РАБОТА № 4
определение моментов инерции параллелепипеда методом крутильных колебаний
САНКТ-ПЕТЕРБУРГ 2003 г.
Цель работы - определить моменты инерции прямоугольного параллелепипеда относительно трех взаимно перпендикулярных осей, проходящих через центр масс, с помощью крутильных колебаний.
Общие сведения
или
где D mi - масса элемента; ri - расстояние от элемента до оси вращения; r - плотность вещества в элементе объема dV, находящегося на расстоянии r от оси вращения. Таким образом, задача нахождения момента инерции сводится к интегрированию. Так как у тела может быть сколько угодно осей вращения, то и моментов инерции может быть бесконечное множество. Наибольший интерес для практики представляют моменты инерции тела относительно трех взаимно перпендикулярных осей О x, О y, О z, проходящих через центр масс. Моменты инерции тела относительно этих осей называются главными моментами инерции:
Моменты инерции однородных тел простейшей формы
Примечание .m- масса тела.
Если тело представляет собой однородный прямоугольный параллелепипед со сторонами а, в, с (рис.2), моменты инерции тела
Здесь оси х, у и z проходят через центр масс перпендикулярно граням со сторонами соответственно bс, ас и аb. Если тело имеет форму куба, то a = b = c и
В общем случае расчет момента инерции представляет собой достаточно сложную задачу, и часто он определяется экспериментально с помощью основного уравнения динамики вращательного движения, методом крутильных колебаний и др. В данной работе момент инерции определяется методом крутильных колебаний. Если тело, висящее на нерастяжимой нити (так, что направление нити проходит через центр тяжести тела), повернуть в горизонтальной плоскости на некоторый угол a, то в результате деформации нити возникнет упругая сила. Она создаст крутящий момент (момент силы) М, возвращающий систему в исходное состояние. В результате возникнут крутильные колебания. Известно, что при небольших отклонениях от равновесия момент М пропорционален углу a. Введя коэффициент пропорциональности D - модуль кручения, зависящий от упругих свойств нити, получим М = - D a. Если пренебречь силами сопротивления, то основной закон динамики вращательного движения можно записать в виде М = - D a = Je. (1) Учитывая, что
уравнение (1) можно привести к виду
Решением уравнения (2) являются функции синуса или косинуса
(здесь
Уравнение (3) тождественно уравнению (2), если
Так как
Так как D неизвестен, для его исключения из формулы (5) следует провести измерения периода колебаний с телом, момент инерции которого относительно оси вращения или легко рассчитывается, или известен. Таким телом может быть, например, куб, момент инерции которого
где m - масса куба, в данном случае m = 0,962 кг; а - длина ребра куба, а = 5,0 см. В установке, используемой для измерений, имеется рамка, конструкция которой позволяет закреплять в ней различные тела, отличающиеся по массе и размерам. Пусть J 0 - момент инерции куба; J р - момент инерции рамки; J - момент инерции параллелепипеда относительно некоторой оси. Тогда на основании формулы (5) получим
где Т р - период колебаний рамки; Т 0 - период колебаний рамки и куба; Т - период колебаний рамки и параллелепипеда. Исключая из уравнений (6) D и J р, запишем
Порядок выполнения работы
Установка состоит из массивного основания со штативом. Кронштейны на штативе служат для закрепления стальной проволоки, на которой подвешена рамка. На среднем кронштейне закреплена стальная плита, являющаяся основанием для фотоэлектрического датчика, электромагнита и шкалы. Положение электромагнита относительно фотоэлектрического датчика указано стрелкой на шкале. Во время колебаний крутильного маятника стрела рамки прерывает световой поток, в результате чего в электронной схеме генерируются импульсы, которые после усиления подаются на электронный секундомер. Последовательность измерений следующая: 1) измерить время t 10 колебаний пустой рамки; вычислить период колебания Т = t/N, где N - число колебаний; 2) повторить измерения не менее 10 раз; 3) установить в рамку куб и повторить пп.1-2 не менее 10 раз; 4) установить в рамку параллелепипед и повторить пп.1-2 не менее 10 раз (период колебаний параллелепипеда измерить для трех взаимно перпендикулярных осей). Результаты, полученные в опыте, следует представить в виде таблицы. Так как в работе производятся многократные измерения, то целесообразно рассчитать средние квадратичные ошибки
где
n - число измерений; Так как
где
где Расчеты погрешностей следует делать для всех трех моментов инерции, а окончательные результаты представить в виде
Средние
Контрольные вопросы
1. В чем заключается физический смысл момента инерции? От чего зависит момент инерции? 2. Как рассчитывается момент инерции? Выведите формулу (5). 3. В чем состоит сущность метода крутильных колебаний? 4. Какими уравнениями описываются крутильные колебания? 5. Какие величины влияют на период колебаний? 6. Почему Т и Т 0 много больше периода рамки? 7. Как рассчитать J 0? 8. Почему у параллелепипеда Jx ¹ Jy ¹ Jz,, а у куба Jx = Jy = Jz? 9. Почему формулу погрешности можно представить в более простом виде (9)?
МЕХАНИКА
ЛАБОРАТОРНАЯ РАБОТА № 5
определение момента инерции с помощью маятника обербека
САНКТ-ПЕТЕРБУРГ 2011 г.
Цель работы - исследовать зависимость момента инерции крестовины с надетыми на нее грузиками от распределения массы относительно оси вращения, проходящей через центр масс. Общие сведения
В основе эксперимента лежит основное уравнение динамики вращательного движения твердого тела
где В динамике вращательного движения различают два понятия: момент силы относительно точки и момент силы относительно оси вращения. Момент силы относительно точки О определяется как векторное произведение
где Момент силы относительно оси вращения есть проекция
Момент инерции тела является мерой инертности тела при вращательном движении, подобно тому как масса тела является мерой инертности тела при поступательном движении. Момент инерции тела зависит от распределения массы тела относительно оси вращения. Для вычисления момента инерции твердого тела относительно данной оси разобьем мысленно тело на большое число весьма малых элементов - материальных точек (рис.1). Тогда момент инерции тела
или
где D mi - масса элемента; ri - расстояние от элемента до оси вращения; r - плотность вещества в элементе объема dV, находящегося на расстоянии r от оси вращения. Таким образом, задача нахождения момента инерции сводится к интегрированию.
Маятник Обербека состоит из крестовины, на стержнях которой находятся грузы. Они могут перемещаться по стержням и закрепляться в нужном положении (рис.2). Крестовина с грузами насажена на вал, на котором укреплены два шкива различного радиуса. На шкив намотана нить, которая переброшена через блок. К ее концу привязана гирька, момент силы тяжести которой уравновешивает момент сил трения (вес этой гирьки в расчетах не учитывается). К концу нити подвешивают груз массой m, под действием силы тяжести которого система приводится в движение. На груз действует сила тяжести P= mg и сила натяжения F, поэтому на основании второго закона Ньютона можно записать
где g - ускорение свободного падения; а - ускорение, с которым движется груз. Крестовина приходит во вращательное движение под действием момента силы натяжения М = Fr о, (3) где r о - радиус шкива. Из уравнений (1)-(3) можно получить
Так как угловое ускорение связано с ускорением а соотношением e = а/r 0, то формулу (4) можно записать в виде
где а = 2 h/t 2; h - путь, пройденный грузом за время t. Таким образом,
Порядок выполнения работы Проверить, что две неподвижные рамки установлены на вертикальной линейке на расстоянии 40 – 50 см друг от друга. Измерить радиус шкива r 0. Последовательность проведения измерений следующая: 1) установить грузы на стержнях на максимальном расстоянии от оси вращения и закрепить их; 2) намотать нить на шкив, установив подвешенный груз на уровне верхней рамки; 3) отпустить груз и измерить время t его движения до нижней рамки (взять не менее трех отсчетов t и вычислить 4) сместить грузы на стержнях на два деления к центру и повторить пп.1-3, измерить расстояние r от оси вращения до центра масс груза; 5) повторить пп.4 для 8-10 положений грузов. Результаты измерений удобно представить в виде табл.1. Таблица 1
__________________ Примечание. J э рассчитывается по формуле (6).
Из теоретических соображений следует, что момент инерции крестовины с четырьмя грузами массой
где J 0 - момент инерции тела при r = 0. Из формулы (7) следует, что J = f (r2). Следовательно, если построить график этой функции в координатах J - r 2, то должна получиться прямая, продолжение которой будет пересекать ось ординат в некоторой точке, соответствующей J 0. Такое построение можно сделать приближенно, «на глаз». Однако математические методы обработки результатов наблюдения позволяют сделать такое построение достаточно точным. Наиболее просто это можно сделать, с помощью метода наименьших квадратов, вычислив J 0 и Для удобства перепишем формулу (7) в виде
где r2 = х и 4 m ' = b. Метод наименьших квадратов позволяет найти J 0 и b:
где Обработку результатов эксперимента удобно вести в форме табл.2. Таблица 2
Рассчитав J 0 и b по формулам (9), следует построить зависимость J от x по формуле (8). Так как через две точки можно провести только одну прямую, то для построения этой прямой можно взять какие-нибудь две удобные точки. Далее по формуле (8) рассчитать момент инерции J p для каждого опыта, заполняя последний столбец табл.1. Среднее квадратичное отклонение
По данным опыта и расчетов следует построить график функции в координатах J - r 2 (8), полученный методом наименьших квадратов, и вычислить доверительный интервал измерения момента инерции в границах
Контрольные вопросы 1. Что такое момент инерции? От чего он зависит? Как можно рассчитать момент инерции? 2. В чем заключается основное уравнение динамики вращательного движения? Что такое момент силы? 3. Что должно измениться в формуле (6), если изменить массу груза m и радиус шкива r 0? 4. Как выглядит график зависимости момента инерции в координатах J - r 2; J - r? Почему результаты опыта лучше обрабатывать в координатах J - r 2? 5. Почему график зависимости J = f (r 2) не проходит через начало координат? Какой смысл имеет величина J 0? 6. Какой смысл имеет тангенс угла наклона графика к горизонтальной оси?
|

 Момент инерции тела является мерой инертности тела при вращательном движении, подобно тому как масса тела является мерой инертности тела при поступательном движении. Момент инерции тела зависит от распределения массы тела относительно оси вращения (см. таблицу). Для вычисления момента инерции твердого тела относительно данной оси разобьем мысленно тело на большое число весьма малых элементов - материальных точек (рис.1). Тогда момент инерции тела
Момент инерции тела является мерой инертности тела при вращательном движении, подобно тому как масса тела является мерой инертности тела при поступательном движении. Момент инерции тела зависит от распределения массы тела относительно оси вращения (см. таблицу). Для вычисления момента инерции твердого тела относительно данной оси разобьем мысленно тело на большое число весьма малых элементов - материальных точек (рис.1). Тогда момент инерции тела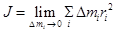
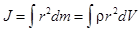 ,
,






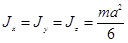 .
.

 . (2)
. (2)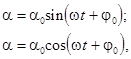
 - амплитудное значение угла отклонения; w - круговая частота;
- амплитудное значение угла отклонения; w - круговая частота;  - начальная фаза), дифференцируя которые два раза по времени, получим
- начальная фаза), дифференцируя которые два раза по времени, получим . (3)
. (3) . (4)
. (4) , где T - период колебаний, то уравнение (4) можно записать в виде
, где T - период колебаний, то уравнение (4) можно записать в виде . (5)
. (5)
 (6)
(6) (7)
(7) для моментов инерции параллелепипеда относительно осей х, у, z. Удобно сначала рассчитать относительную ошибку
для моментов инерции параллелепипеда относительно осей х, у, z. Удобно сначала рассчитать относительную ошибку  . На основании формул теории погрешности (необходимо уметь выводить это соотношение)
. На основании формул теории погрешности (необходимо уметь выводить это соотношение) (8)
(8)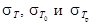 - средние квадратичные ошибки,
- средние квадратичные ошибки,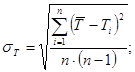
 - среднее значение соответствующего периода колебаний;
- среднее значение соответствующего периода колебаний;  - период, найденный в каждом опыте.
- период, найденный в каждом опыте. , то формулу (8) можно записать в виде
, то формулу (8) можно записать в виде , (9)
, (9) - средняя квадратичная ошибка момента инерции куба,
- средняя квадратичная ошибка момента инерции куба,

 - ошибка при измерении массы,
- ошибка при измерении массы,  - приборная ошибка,
- приборная ошибка,  = 1 мм.
= 1 мм.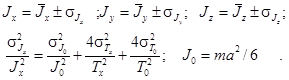
 ,
,  и
и  рассчитать по формуле (7).
рассчитать по формуле (7). (1)
(1) - суммарный момент внешних сил, приложенных к телу относительно оси вращения; J - момент инерции тела относительно той же оси;
- суммарный момент внешних сил, приложенных к телу относительно оси вращения; J - момент инерции тела относительно той же оси;  - угловое ускорение.
- угловое ускорение. ,
, - сила,
- сила,  - радиус-вектор, проведенный из точки О, в точку приложения силы.
- радиус-вектор, проведенный из точки О, в точку приложения силы. на произвольную ось z, которая проходит через точку О:
на произвольную ось z, которая проходит через точку О:

 .
.
 ,
, Из формулы (1) следует, что угловое ускорение e вращающегося тела прямо пропорционально моменту внешних сил М и обратно пропорционально моменту инерции J. Следует подчеркнуть, что момент инерции не зависит ни от момента внешних сил М, ни от углового ускорения.
Из формулы (1) следует, что угловое ускорение e вращающегося тела прямо пропорционально моменту внешних сил М и обратно пропорционально моменту инерции J. Следует подчеркнуть, что момент инерции не зависит ни от момента внешних сил М, ни от углового ускорения. (2)
(2) , (4)
, (4) , (5)
, (5) (6)
(6) );
);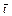
 , если считать грузы материальными точками, можно выразить формулой
, если считать грузы материальными точками, можно выразить формулой (7)
(7)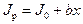 , (8)
, (8) (9)
(9) число опытов; Ji - экспериментальное значение момента инерции J э, полученное для каждого опыта (табл.1).
число опытов; Ji - экспериментальное значение момента инерции J э, полученное для каждого опыта (табл.1).




 .
. .
.


