Термохимические расчеты
Факультет экономики и управления
В основе термохимических расчетов лежит закон Гесса, устанавливающий независимость тепловых эффектов изобарных и изохорных процессов от пути проведения (промежуточных стадий) этих процессов. Использование этого закона дает возможность определять тепловые эффекты таких процессов, которые не удается изучить непосредственно, а также позволяет рассчитывать тепловые эффекты на основе использования стандартных энтальпий образования (
где индексы j и i использованы для обозначения начальных и конечных веществ соответственно. В термодинамической системе знаков положительные значения тепловых эффектов соответствуют эндотермическим процессам (тепло поглощается). Расчет тепловых эффектов при температурах, отличных от стандартной (298 К), проводят с использованием истинных (Сp) или средних (
Связь между этими параметрами задается уравнением:
Величины При расчетах с использованием средних теплоемкостей необходимо применять только те значения Зависимость Cp = f(T) обычно представляют в форме многочлена (полинома) с эмпирическими коэффициентами. Для простых и неорганических веществ:
Для органических веществ:
Для расчета тепловых эффектов применяют уравнение Кирхгоффа с использованием истинных или средних теплоемкостей:
где Значения коэффициентов полиномов Сp = f(T) имеются в справочниках.
|

 ), имеющихся в справочной литературе. В последнем случае расчет стандартного теплового эффекта (
), имеющихся в справочной литературе. В последнем случае расчет стандартного теплового эффекта ( ) некоторого процесса
) некоторого процесса  следует проводить по уравнению:
следует проводить по уравнению: ,
,
 ) теплоемкостей, определяемых соотношениями:
) теплоемкостей, определяемых соотношениями: ;
;  .
.
 .
.
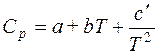

 ,
,
 .
.


