Критерий совместности Кронекера-Капелли
Суть этого метода состоит в том, что посредством последовательного исключения неизвестных матрица системы превращается в треугольную, равносильную данной. Удобнее приводить к трапециевидному виду расширенную матрицу системы, выполняя элементарные преобразования над ее строками. Пример. Решить систему уравнений методом Гаусса:
3x1 – 2x2 + x3 = - 1, 2x1 + x2 – 2x3 = 0. Решение. Выпишем расширенную матрицу данной системы и произведем следующие элементарные преобразования над ее строками: а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2: б) третью строку умножим на (-5) и прибавим к ней вторую:
x1 + x2 – 3x3 = 2, -5x2 + 10x3 = -7, - 10x3 = 13. Из последнего уравнения находим x3 = -1,3. Подставляя это значение во второе уравнение, имеем x2 = -1,2. Далее из первого уравнения получим x1 = - 0,7.
Решение систем линейных уравнений Критерий совместности Кронекера-Капелли Система линейных уравнений имеет вид:
где а ij – коэффициенты при неизвестных, bi – свободные члены м(i = Решением системы называется такая совокупность n чисел (x1=c1, x2=c2,..., xn=cn), при подстановке которых каждое уравнение системы обращается в верное равенство. Система уравнений называется совместной, если она имеет хотя бы одно решение. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. Система называется несовместной, если она не имеет решений. Пример: - система уравнений - система уравнений - система уравнений Запишем систему уравнений в матричной форме AX = B, где Если к матрице системы приписать столбец свободных членов, то получится расширенная матрица системы вида
Вопрос о совместности системы решается следующей теоремой. Теорема Кронекера-Капелли: Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы. Система имеет единственное решение только в том случае, когда ранг матрицы совместной системы равен числу переменных r(A) = n. Если ранг матрицы совместной системы меньше числа переменных, то система неопределенная и имеет бесконечное множество решений.
|

 x1 + x2 – 3x3 = 2,
x1 + x2 – 3x3 = 2,
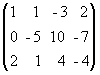 ;
; .
. В результате всех этих преобразований данная система приводится к треугольному виду:
В результате всех этих преобразований данная система приводится к треугольному виду:
 ; j =
; j =  ), xj - неизвестные.
), xj - неизвестные. совместная и определенная, так как имеет единственное решение (10; 0);
совместная и определенная, так как имеет единственное решение (10; 0); несовместная;
несовместная; совместная и неопределенная, так как имеет более одного решения (x1=c, x2=10-2c), где с – любое число.
совместная и неопределенная, так как имеет более одного решения (x1=c, x2=10-2c), где с – любое число. - матрица коэффициентов при неизвестных, называемая матрицей системы,
- матрица коэффициентов при неизвестных, называемая матрицей системы,  - столбец переменных,
- столбец переменных,  столбец свободных членов.
столбец свободных членов. .
.


