Уравнение состояния атмосферы
Всякий газ оказывает механическое воздействие на ограничивающую его поверхность. Это воздействие называется силой. Модуль силы, действующей на единичную, площадку, называется давлением. Если внутри атмосферы выделить любой, сколь угодно малый объем, то на его внешние границы будет оказывать давление внешняя часть атмосферы. В свою очередь, это давление будет уравновешиваться внутренним давлением воздуха, направленным наружу. Термодинамическое состояние атмосферы, являющейся смесью газов, достаточно точно описывается уравнением Клапейрона для идеального газа, т.е. газа, в котором силы внутреннего трения пренебрежимо малы по сравнению с внешними силами. Это уравнение имеет вид:
PV=RT (1.1) где P – атмосферное давление; V – удельный объем газа, т.е. величина, определяемая отношением объема тела к его массе; R – удельная газовая постоянная, зависящая от природы газа; T – температура по абсолютной шкале Кельвина.
В метеорологии принята определенная система измерения различных физических величин. Атмосферное давление на метеорологических станциях измеряется в гектопаскалях (гПа), 1 Па = 1 н/м2. Нормальное атмосферное давление на уровне моря составляет 1013 гПа, что соответствует 760 мм рт. ст. в системе единиц, применявшихся ранее. Диапазон изменения давления по данным наблюдений находится в пределах от 800 до 1100 гПа. Температура воздуха измеряется в градусах шкалы Цельсия (ºC) и обозначается буквой t. В этой шкале нуль приходится на температуру таяния льда, а 100ºC – на температуру паров кипящей воды при давлении 1013 гПа. У земной поверхности температура воздуха колеблется в пределах от 60ºC в тропиках до -90ºC в центральных районах Антарктиды. При расчетах, связанных с термодинамическими процессами используется шкала Кельвина. Нуль шкалы Кельвина соответствует точке полного прекращения движения молекул ºК= -273,15ºC Шаг шкалы Цельсия равен шагу шкалы Кельвина, 1К=1ºC. В формулах абсолютная температура обозначается T, таким образом
T = t +273,15
Уравнение (1.1) можно переписать в виде P = ρ×R×T, где ρ= 1 / V, – плотность воздуха, т.е. величина обратно пропорциональная удельному объему, или r = P/R×T (1.2) Плотность воздуха может быть вычислена из уравнения состояния газа. Численное значение газовой постоянной для сухого воздуха Rd составляет 287,05 Дж/(кг×К). Если имеется влажный воздух с температурой T, давлением P и давлением водяного пара e, то можно найти выражение для его плотности ρ;. Если представить влажный воздух как смесь сухого воздуха и водяного пара, то из общего давления воздуха P на долю сухого воздуха приходится величина P–e. Тогда для сухого воздуха уравнение (1.2) можно записать в виде Молекулярная масса сухого воздуха, вычисленная на основе его газового состава составляет 28,97 кг/кмоль, а молекулярная масса водяного пара 18,02 кг/кмоль, таким образом, отношение молекулярной массы водяного пара к молекулярной массе воздуха равно 0,622. Исходя из этого соотношения для водяного пара, находящегося в смеси с сухим воздухом можно записать
Так как общая плотность влажного воздуха равна сумме плотностей сухого воздуха и водяного пара, то
Ввиду малости величины отношения
поскольку величина
Выражение 1+0,378 Виртуальная температура влажного воздуха есть такая температура, которую должен был бы иметь сухой воздух, чтобы его плотность равнялась плотности влажного воздуха с температурой T, давлением P и влажностью e. Виртуальная температура всегда несколько выше истинной температуры влажного воздуха. Из уравнения (1.6) вытекает, что влажный воздух несколько менее плотен, чем сухой при тех же значениях давления и температуры (рис. 1.2). Разница в плотности не очень велика. Для сухого воздуха при t = 0ºC и P = 1000 гПа ρ = 1,276 кг/м3. При том же давлении и температуре, но при полном насыщении, при e = 6.1 гПа, ρ= 1,273 кг/м3.
Рис. 1.2. Убывание атмосферного давления с высотой в зависимости от температуры воздушного столба
Плотность воздуха в каждой точке атмосферы непрерывно изменяется во времени. Она изменяется и с высотой, поскольку изменяются температура воздуха и атмосферное давление. Падение температуры вызывает увеличение плотности воздуха, однако, атмосферное давление с высотой уменьшается. В результате совместного действия этих двух факторов плотность воздуха с высотой уменьшается не так быстро, как давление. Характер изменения плотности воздуха ρ; при изменении высоты z представлен в табл. 1.2. Таблица 1.2 Изменение плотности воздуха с высотой
Если бы плотность воздуха не изменялась с высотой и на всех уровнях оставалась такой же, как у земной поверхности, то при нормальном атмосферном давлении на уровне моря 1013 гПа, убывающем по линейному закону, определяемому формулой
P2 = P1–ρg( Z 2– Z 1),
где: P1 и P2 – атмосферное давление на уровнях Z1 и Z2 соответственно; g = 9,80665 м/с2 – ускорение силы тяжести; ρ = 1,276 кг/м3 – плотность воздуха, высота атмосферы составила бы примерно 8000 м.
Подразумевается, что при этих условиях в соответствии с уравнением состояния атмосферы, температура в столбе воздуха убывает на 3,42ºC на каждые 100 м увеличения высоты. Такое строение атмосферы называется однородной атмосферой и используется при некоторых приближенных вычислениях, а высота 8000 м называется высотой однородной атмосферы.
|

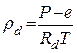 , где Rd – газовая постоянная для сухого воздуха.
, где Rd – газовая постоянная для сухого воздуха.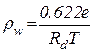 (1.3)
(1.3)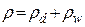 , откуда
, откуда  , или
, или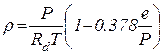 (1.4)
(1.4) ,
,  используя известную алгебраическую формулу
используя известную алгебраическую формулу  , уравнение (1.4) можно записать в виде
, уравнение (1.4) можно записать в виде (1.5)
(1.5)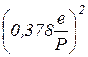 пренебрежимо мала по сравнению с единицей, входящей в формулу (1.5), то
пренебрежимо мала по сравнению с единицей, входящей в формулу (1.5), то 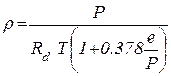 , если обозначить
, если обозначить 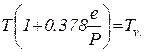 , где Tv – виртуальная температура, то в окончательном виде формула (1.5) принимает вид
, где Tv – виртуальная температура, то в окончательном виде формула (1.5) принимает вид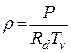 (1.6)
(1.6) называется виртуальным добавком. Уравнение (1.6) позволяет определить состояние влажного воздуха при помощи уравнения состояния сухого воздуха с заменой истинной температуры на ее виртуальную величину.
называется виртуальным добавком. Уравнение (1.6) позволяет определить состояние влажного воздуха при помощи уравнения состояния сухого воздуха с заменой истинной температуры на ее виртуальную величину.



