Статика атмосферы. Барометрическая формула
Если выделить из атмосферы вертикальный столб площадью поперечного сечения равной единице и в нем некоторый элементарный слой dZ, ограниченный снизу высотой Z, а сверху высотой Z+dZ (рис. 1.3), то на нижнюю поверхность выделенного элементарного объема внешний по отношению к нему воздух воздействует с силой давления, направленной снизу вверх. При площади поверхности равной единице эта сила равняется атмосферному давлению P на высоте Z. На верхнюю поверхность, расположенную на высоте Z+dZ, внешний воздух воздействует сверху вниз с силой –(P+dP). Сам элементарный объем воздуха действует силой, направленной вниз. Величина этой силы определяется выражением gρdZ, где g – ускорение силы тяжести, ρ; – плотность воздуха, dZ – элементарный объем при пощади столба равной единице.
Рис. 1.3. Силы, действующие на единичный объем воздуха
Если в горизонтальном направлении атмосферное давление не изменяется, то равнодействующая боковых сил равна нулю. Поскольку выделенный объем находится в состоянии статического равновесия, сумма действующих на него сил должна быть равна нулю, т.е. –(P+dP)+ P–gρdZ = 0, откуда
Если dZ положительно, то dP имеет отрицательное значение, что означает падение атмосферного давления с высотой. Разность давлений на нижней и верхней границе выделенного объема уравновешивается силой тяжести, воздействующей на воздух, заключенный в этом объеме. Уравнение (1.7) называется основным уравнением статики атмосферы. Оно показывает, как изменяется атмосферное давление при малом приращении высоты. Это уравнение можно переписать в виде Величина Правая часть выражения (1.7) представляет собой силу тяжести, действующую на единицу массы и направленную вниз. Таким образом, основное уравнение статики выражает условие равновесия между силами, действующими на единицу массы по вертикали: барическим градиентом и силой тяжести. Для того, чтобы получить выражение, определяющее величину изменения давления при конечном приросте высоты, необходимо проинтегрировать уравнение (1.7) в пределах от высоты Z1 с давлением P1 до высоты Z2 с давлением P2. При интегрировании этого уравнения следует учесть, что плотность воздуха ρ; также является переменной величиной, зависящей от высоты Z. Она может быть выражена через уравнение состояния атмосферы (1.2).
подставив это выражение в уравнение (1.7), получим
или
Результат интегрирования уравнения (1.10) с учетом того, что R и g являются постоянными величинами, примет вид
проинтегрировав левую часть уравнения (1.11) получим
Находящаяся в правой части выражения (1.12) температура воздуха T является переменной величиной, зависящей от высоты Z, так же, как и величина ρ в формуле (1.7). Характер изменения температуры с высотой достаточно сложен и не может быть выражен математическим уравнением. По этой причине ее целесообразно заменить средним значением температуры атмосферного столба Tm, , величина которой может быть определена на основе метеорологических измерений. С учетом такой замены выражение (1.12) примет вид
откуда
После выполнения операции потенцирования предыдущее выражение примет вид
Уравнение (1.15) является интегралом основного уравнения статики атмосферы. Оно называется также барометрической формулой, поскольку связывает изменение атмосферного давления с высотой в зависимости от температуры воздуха. Основное уравнение статики атмосферы основано на допущении о том, что некоторый объем воздуха находится в равновесии по вертикали. В действительности во многих случаях существует некоторая вертикальная составляющая равнодействующая силы тяжести и барического градиента, отличная от нуля. Как правило, эта сила незначительна, поэтому основное уравнение статики выполняется с большой степенью точности, хотя и не абсолютно строго. Барометрическая формула в различных своих вариантах позволяет решать три важные задачи. 1. Если известны атмосферное давление на одном уровне и средняя температура столба воздуха, можно определить атмосферное давление на другом уровне. 2. По известным значениям температуры воздушного столба и атмосферного давления на двух различных уровнях определить разность уровней. Эта задача обычно называется барометрическим нивелированием. 3. По известным разностям уровней и величинам атмосферного давления на этих уровнях определить среднюю температуру столба воздуха. Для практического использования барометрическая формула приводится к рабочему виду. С этой целью натуральные логарифмы пересчитываются в десятичные, абсолютная температура в Кельвинах заменяется на градусы Цельсия, постоянные величины приводятся к единому коэффициенту. При этом для влажного воздуха принимается в расчет удельная газовая постоянная Rd для сухого воздуха, а температура воздушного столба заменяется его виртуальной температурой. Кроме того, в величину атмосферного давления вводятся поправки за широту местности и высоту над уровнем моря. Для метеорологических наблюдений наиболее важным является первый вариант использования барометрической формулы. Ее использование разрешает привести атмосферное давление к уровню моря. Задача заключается в том, что для составления синоптических карт и прогнозов атмосферное давление должно быть приведено к некоторому единому уровню. В этом случае возможно сравнение состояния атмосферы в различных точках земного шара. Для этого атмосферное давление, измеренное на метеорологических станциях и обсерваториях, расположенных на различных высотах, приводится к уровню моря. С этой целью по измеренным значениям температуры воздуха t и атмосферного давления P на метеорологической станции, расположенной на высоте H над уровнем моря, на первом этапе вычисляется некоторая температура, которая могла бы иметь место, если бы эта метеостанция располагалась на уровне моря при H =0. Эта температура носит условный характер, поскольку метеорологическая станция может быть расположена достаточно далеко от моря. Для определения температуры воздуха на уровне моря, соответствующей температуре, измеренной на метеорологической станции, используется среднее значение вертикального градиента температуры, равное 0,6ºС/100 м. Если метеорологическая станция расположена на высоте 600 м над уровнем моря и на ней измерена температура воздуха, равная +20ºС, то на уровне моря соответствующая ей температура составила бы +23,6ºС. В этом случае средняя температура воздушного столба составит +21,8ºС. Эта величина принимается за основу для расчета атмосферного давления на уровне моря. Во избежание большого количества однотипных вычислений на каждой метеорологической станции составляется специальная таблица поправок за приведение атмосферного давления к уровню моря. Барометрическое нивелирование применяется в основном в горных местностях, там, где основные методы геодезии не могут быть использованы ввиду сложности рельефа. После указанных выше преобразований формула барометрического нивелирования принимает вид
где: α – объемный коэффициент расширения воздуха, α; = 1/273,15 = 3,66.10-3 (ºС)-1; P1 и P2 – атмосферное давление в пунктах 1 и 2 соответственно; t – средняя температура воздушного столба (ºС)..
Погрешности барометрического нивелирования в основном связаны с тем обстоятельством, что температура воздуха измеряется только в пунктах измерения атмосферного давления, что не в полной мере отражает реальное изменение температуры между пунктами измерений. Кроме того, не во всех случаях удается обеспечить синхронность измерений в обоих пунктах. Основное уравнение статики атмосферы (1.7) может быть записано в виде
Отношение Подставив в формулу (1.16) численные значения g и R, можно вычислить барическую ступень для различных величин P и T. Если температура воздуха t =0ºС и атмосферное давление P =1000 гПа, барическая ступень составит 8 м. Другими словами, при данных атмосферных условиях, на высоте 8 м от исходной поверхности давление будет меньше на 1 гПа. С увеличением температуры барическая ступень увеличивается на 0,4% на каждый градус. На высоте 5000 м, где P =500 гПа при t =0ºС барическая ступень равна 16 м/гПа. Зная величину барической ступени для различных значений P и t, можно легко производить расчеты по барометрической формуле, если разность высот не очень велика. Атмосферное давление меняется не только с изменением высоты. оно изменяется и на одном и том же уровне в различных точках местности. Кроме того, в каждой точке атмосферное давление непрерывно изменяется во времени. Таким образом, во всей атмосфере постоянно происходит процесс изменения давления. Изменения температуры и влажности воздуха также приводят к изменению давления. Колебания атмосферного давления вызывают движение воздушных масс, которое, в свою очередь, вызывают изменения давления в конкретных точках. Таким образом, весь воздух, находящийся в атмосфере, непрерывно перемещается. В то же время, на основе многолетних наблюдений можно статистически достаточно устойчивую связь между атмосферным давлением и высотой. Для европейской части нашего материка эта зависимость представлена в табл. 1.3. Таблица 1.3 Зависимость атмосферного давления от высоты
График связи атмосферного давления с высотой, построенный по приведенным выше данным представлен на рис. 1.4. Из рассмотрения этого графика со всей очевидностью вытекает, что при возрастании высоты в арифметической прогрессии атмосферное давление убывает в геометрической.
Рис. 1.4. Изменение атмосферного давления с высотой Зная величину атмосферного давления на уровне моря можно вычислить общую массу атмосферы. Поскольку давление есть сила, она по определению равна массе, умноженной на ускорение силы тяжести, массу атмосферы Mатм можно вычислить по формуле
где P = 101300 Па – атмосферное давление на уровне моря; S = 5,101×1014 м2 – площадь поверхности земного шара; g = 9,80665 м/с– ускорение силы тяжести.
Подставив приведенные исходные данные в приведенную выше формулу, получим С учетом того, что материки возвышаются над уровнем Мирового океана и атмосферное давление над ними несколько ниже, реальная масса атмосферы равна 5,157×1015т. Масса Земли Mз =5,98×1021т, откуда
|


 (1.7)
(1.7) .
. называется вертикальным барическим градиентом или вертикальным градиентом давления. Она определяет падение атмосферного давления на единицу высоты. Вертикальный барический градиент является равнодействующей сил давления, действующих на единичный объем воздуха. Разделив его на плотность воздуха ρ; получим
называется вертикальным барическим градиентом или вертикальным градиентом давления. Она определяет падение атмосферного давления на единицу высоты. Вертикальный барический градиент является равнодействующей сил давления, действующих на единичный объем воздуха. Разделив его на плотность воздуха ρ; получим  – вертикальный барический градиент, отнесенный к единице массы и направленный вверх
– вертикальный барический градиент, отнесенный к единице массы и направленный вверх , (1.8)
, (1.8) (1.9)
(1.9) , (1.10)
, (1.10)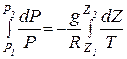 , (1.11)
, (1.11)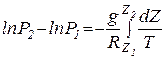 , (1.12)
, (1.12) , (1.13)
, (1.13) , (1.14)
, (1.14) (1.15)
(1.15)
 , где Δh – превышение между пунктами 1 и 2,
, где Δh – превышение между пунктами 1 и 2, , (1.16)
, (1.16) называется барической ступенью. По своей сути барическая ступень является величиной, обратной вертикальному барическому градиенту
называется барической ступенью. По своей сути барическая ступень является величиной, обратной вертикальному барическому градиенту 
 ,
, .
. .
.


