Основные расчетные формулы. Полоса пропускания системы вычисляется по следующим выражениям
Токи контуров Частоты связи Полоса пропускания системы вычисляется по следующим выражениям
Токи на частоте индивидуального резонанса зависят от связи:
РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ
Результаты измерений АЧХ системы двух колебательных контуров при различных значения фактора связи приведены в таблицах 3.1 – 3.4. Таблица 3.1 – Результаты измерений при А=0.
Таблица 3.2 – Результаты измерений при А=0,5.
Таблица 3.3 – Результаты измерений при А=1.
Таблица 3.4 – Результаты измерений при А=2,41.
Вычислим коэффициент прямоугольности для всех приведенных случаев. При А=0:
При А=0,5:
При А=1:
При А=2,41:
Построим график зависимости Зависимости приведены на рисунке 3.1:
Рис. 3.1 – График зависимости
[ Рис. 3.1 – График зависимости
Исследование влияния второго контура на первый
max M при А=1,
при А=0 Построим график зависимости
Рис. 3.2 - График зависимости
При А=0,5:
При А=1:
При А=2,41:
ВЫВОДЫ В результате работы исследовались частотные характеристики двух колебательных контуров в зависимости от связи между ними. Из построенных графиков видно, что при влиянии одного контура на другой полоса пропускания,при увеличении фактора связи А,расширяется. Увеличение фактора связи А приводит к увеличению коэффициента прямоугольности Критическому значению А=1 соответствует оптимальной связи между контурами. Это настройка в полный резонанс. При этом При А>1 нормированное значение тока во втором контуре падает ниже уровня 0,707 на резонансной частоте от максимально возможного значения, что и приводит к разделению АЧХ на два участка. Частотные зависимости для первого и второго контуров похожи.
|

 ,
,  (2.1)
(2.1) (2.2)
(2.2)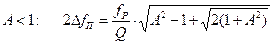 (2.3)
(2.3) (2.4)
(2.4) (2.5)
(2.5)
 ;
; 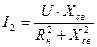 ; (2.6)
; (2.6)

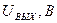



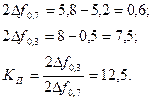
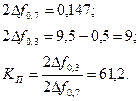
 для разных факторов связи, при которых были сняты данные с прибора Х1-40.
для разных факторов связи, при которых были сняты данные с прибора Х1-40.

 .
.




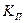 . Это связано с увеличением добротности контура и
. Это связано с увеличением добротности контура и  .
.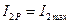 . При А=2,41 АЧХ передаточной функции разделяется на две части.
. При А=2,41 АЧХ передаточной функции разделяется на две части.


