Решаем методом неопределенного множителя Лагранжа.L = T + β[SСПД – S*] β; – параметр Лагранжа Если мы найдем вектор пропускных способностей, который бы минимизировал L, то он же минимизирует T при выполнения ограничений [SСПД – S*]. И этот вектор является искомым решением.
Считаем частную производную от функции, для которой ищем экстремум.
При определенных видах стоимостных функция уравнение (*) решается аналитическим методом вместо численного.
β; -?
Обратная задача Формируется при тех же исходных данных: 1. СПД, состоящей из N центров коммутации и M каналов связи 2. Потоки в каналах связи лямбда 3. Длина сообщений (может быть определена по среднему значению) 4. Стоимостные функции КС Si(Ci), 5. Т* – Пороговое значение задержки передачи данных в СПД.
|
(*)
- трафик, поступающий в КС [бит/сек]
- минимум необходимых средств для построения сети с минимальной пропускной способностью.
- дополнительные средства, выделенные сверх необходимых.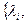
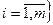
, где Ci – пропускная способность, Si – стоимость построения
Найти вектор 
(где С1, С2, …, Сk – оптимальные значения для каждого канала) пропускных способностей для каждого канала, который бы минимизировал стоимость построения сети при выполнении ограничения на задержку передачи данных.
, 
