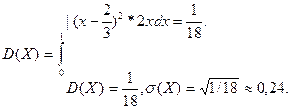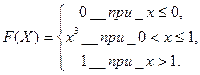Дисперсия случайной величины. Среднее квадратическое отклонение
1. Теле - и аудиоаппаратура, CD (учебные программы) доступ к сети Интернет (во время самостоятельной подготовки). Интернет-ресурсы
ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ ПО ДИСЦИПЛИНЕ «Иностранный язык (специальные тексты)» (французский)
Подписано в печать _______. Формат 60´84/16. Бумага для множ. аппаратов. Печать плоская. Усл. печ. л. 1,860. Уч.-изд. л. 1,986. Тираж экз. Заказ № __. ФГАОУ ВПО «Российский государственный профессионально-педагогический университет». Екатеринбург, ул. Машиностроителей, 11. Ризограф ФГАОУ ВПО РГППУ. Екатеринбург, ул. Машиностроителей, 11. Ответы 1. 2,85. 2. 9, 18,3. 3. 11,3. 4. 48. 5. 17. 6. 1/7. 7. 0,75 .8. 4,5. 9. 1/α. Вопросы 1.Как определяется математическое ожидание дискретной случайной величины X, принимающей конечное множество значений? 2. Какие другие названия используют для математического ожидания? Чем объясняются эти названия? 3. Что называют математическим ожиданием дискретной случайной величины X, принимающей счетное множество значений? 4. Как определяется математическое ожидание непрерывной случайной величины, все значения которой принадлежат отрезку [α,β] 5. Как определяется математическое ожидание непрерывной случайной величины, все значения которой принадлежат бесконечному промежутку (- 6. Каковы свойства математического ожидания случайной величины? 7. Какому условию должны удовлетворять случайные величины X и Y, чтобы выполнялось равенство (2.4.15)? 8. Докажите, что математическое ожидание неотрицательной дискретной величины неотрицательно. Дисперсия случайной величины. Среднее квадратическое отклонение Разность Х—М(Х) называется отклонением случайной величины X от ее математического ожидания М(Х). Математическое ожидание отклонения равно нулю:
М(Х-М(Х))=0. (2.5.1)
Дисперсией, или рассеянием, случайной величины X называемся математическое ожидание квадрата ее отклонения: D(Х) = M((Х - М(Х))2). (2.5.2) Из определения и свойств математического ожидания следует, что дисперсия любой случайной величины неотрицательна, т.е. D(Х) D(X)=M(X2)-(M(X))2. (2.5.4) Дисперсия случайной величины обладает следующими свойствами: 1. Дисперсия постоянной величины равна нулю: D(С) = 0 (С = соnst). (2.5.5) 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D(СХ) = С 2 D(Х) (С = соnst). (2.5.6) 4. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: D(Х + У) = D(Х) + D(У). (2.5.7) 5. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: D(X-У)= D(Х)+D(У). (2 5.8) 3 а м e ч а н и e. Свойство 3 распространяется на n независимых случайных величин: D(X1+ Х2 +... + Хn ) = D (Х1) +D (Х2) +...+D(Хn). (2.5.9) P(X=xk)=pk (k=1,2,...,/1),
определяется формулой D(X)= или формулой
D(X)= где а = М(Х) (2.5.11) - другое обозначение для математического ожидания. Этим обозначением будем пользоваться и в дальнейшем, в зависимости от обстоятельств. Если дискретная случайная величина принимает бесконечную последовательность значений с законом распределения P(X=xk)=pk (k=1,2,3,…)
то ее дисперсия определяется формулой
D(X)=
при условии, что этот ряд сходится. Дисперсия непрерывной случайной величины X, все значения которой принадлежат отрезку [α,β], определяется формулой
D(X)=
где р(х) - плотность распределения вероятностей этой величины, а = М(Х) - ее математическое ожидание. Дисперсию можно вычислять по формуле
D(X)=
Дисперсия непрерывной случайной величины X, всё внимания которой принадлежат отрезку (-
D(X)=
если этот несобственный интеграл сходится абсолютно.
Средним квадратическим отклонением, или стандартным отклонением, случайной величины X называется корень квадратный из ее дисперсии:
Это определение имеет смысл, поскольку выполнено условие (2.5.3). Пример 1. Доказать формулы (2.5.1) и (2.5.4). Решение. Так как математическое ожидание М(Х) - постоянная величина, математическое ожидание постоянной равно этой постоянной, математическое ожидание разности случайных величин равно разности их математических ожиданий, то
M(X-M(X))=M(X)-M(M(X))=M(X)-M(X)=0;
равенство (2.5.1) доказано. Учитывая свойства математического ожидания, получаем
D(X)=M((X-M(X))2)=M(X2-2XM(X)+(M(X))2)= =М(Х2)-2М(ХМ(Х))+M((М(Х))2)=М(Х2)-2М(Х)М(Х) + (М(Х))2 = М(Х2)-(М(Х))2, равенство (2.5.4) доказано. Пример 2. Доказать равенства (2.5.5) - (2.5.8). Решение. Принимая во внимание определение дисперсии и тот факт, что математическое ожидание постоянной равно этой постоянной, получаем
D(C)=M((C-M(C))2)=M((CX-CM(X))2)= =M(C2*(X-M(X))2)=C2M((X-M(X))2)=C2D(X). Для доказательства формулы (2.5.8) воспользуемся формулой (2.5.4):
D(X+Y)=M((X+Y)2)-(M(X+Y))2=M(X2+2XY+Y2)-(M(X)+M(Y))2=M(X2)+M(2XY)-M(Y2)-[(M(X))2+2M(X)M(Y)+(M(Y))2]=M(X2)+2M(X)M(Y)+M(Y2)-(M(X))2-2M(X)M(Y)-(M(Y))2= =M(X2)-(M(X))2+M(Y2)-(M(Y))2=D(X)+D(Y).
Равенство (2.5.8) следует из формул (2.5.6) и (2.5.7): D(Х - У) = D (Х + (-Y)) = D (Х) +D(-У) - D (Х) + (-1)2 D(У) = D (Х) +D(У).
Пример 3. Дискретная случайная величина А' имеет закон распределения
Найти дисперсию и среднее квадратическое отклонение случайной величины X. Решение. По формуле (2.4.3) находим
М(Х)=0*0,3+1*0,5+2*0,2=0,9.
Запишем закон распределения квадрата отклонения этой величины, т.е. величины (X -М(Х)}2:
По формуле (2.5.10) получаем D(Х) = (0 - 0,9)2 • 0,3 + (1 - 0,9)2 • 0,5 + (2 - 0,9)2 0,2 = = 0,81 • 0,3 -4- 0,01 • 0,5 4-1,21 • 0,2 = 0,49. В соответствии с формулой (2.5.16) находим среднее квадратическое отклонение σ(Х) = Замечание. Дисперсию можно вычислить и по формуле (2.5.4). Найдем для этого математическое ожидание квадрата случайной величины X, предварительно записав закон распределения случайной величины X2:
По формуле (2.4.3) находим М(X2) = 0 0,3 + 1-0,5 + 4 0,2 = 1,3. В соответствии с формулой (2.5.4) находим D(Х) = М(Х2)-(М(Х))2 =1,3-0,92 = 1,3-0,81 = 0,49.
Пример 4. Закон распределения дискретной случайной величины X задан таблицей
Вычислить дисперсию случайной величины X по формуле (2.5.4) и по формуле (2.5.10). Решение. Сначала найдем математическое ожидание случайной величины X: М(Х) = -2 • 0,1 -1 • 0,2 + 0 • 0,4 + 1 • 0,2 + 2 • 0,1 = 0. Запишем закон распределения случайной величины (X - М(Х))2:
и найдем дисперсию случайной величины X по формуле (2.5.10): D (Х) = 4 • 0,1 +1 • 0,2 + 0 • 0,4 +1 • 0,2 + 4 - 0,1 = 1,2.
Квадрат случайной величины X т.е. X2 - это новая случайная величина, которая с теми же вероятностями, что и случайная величина Л", принимает значения, равные квадратам ее значений. Квадраты значений случайной величины X равны: (-2)2=4, (-1)2=1, 02=0, 12=1, 22 =4, т.е. величина X2 принимает значения х1 = 0, х2 = 1, х 3 = 4. Закон распределения случайной величины X2 можно записать в виде:
Вероятность 0,4 для значения х2 = 1 получена по теореме сложения вероятностей, с которыми случайная величина X принимает значения -1 и 1. аналогично получена вероятность 0,2 для значения х 3 = 4.
По формуле (2.4.3) находим М(Х2) = 0 • 0,4 +1* 0,4 + 4 • 0,2 = 1,2. Следовательно, по формуле (2.5.4) имеем
D(X)=M(X2)-(M(X))2=1,2-0=1,2.
Пример 5. Симметричная монета подбрасывается 4 раза. Случайная величинаX- "число выпадений герба при этих подбрасываниях". Найти числовые характеристики случайной величины X: М(Х), D (Х), σ (Х). Решение. Данная дискретная случайная величина X может принимать 5 значений х1=0,х2=1,х3=2,х4=3,х5=4.
Закон распределения случайной величины (Х-М(Х))2 имеет вид:
Находим математическое ожидание М(Х): М(Х) = 0-1/16 + 1-4/16 + 2 -6/16 + 3- 4/1 6 + 4 -1/16 =2. Закон распределения случайной величины (X - М(Х))2 имеет вид:
Вычислим дисперсию D(X) и среднее квадратическое отклонение σ(Х) D(X)= 4 -1/16 + 1 • 4/164- 0 • 6/16 + 1-4/16 ч- 4 -1/16 = 1, σ(Х)= Пример 6. Найти дисперсию дискретной случайной величины X - числа очков, выпадающих при подбрасывании игрального кубика. Решение. Запишем сначала закон распределения этой случайной величины в виде таблице
Найдем математические ожидания М(Х) и М(Х2):
М(Х)=1*
М(Х2)= 1*
Дисперсию вычислим по формуле (2.5 4):
D(X)=M(X2)-(M(X))2= Пример 7. Даны все возможные значения дискретной случайной величины Х: х1=1,х2=2,х3=3,а также известны М(Х)=2,3, М(Х2)=5,9. Найти закон распределения случайной величины Х.
Решение. Запишем законы распределения дискретных случайных величин X и X 2:
Где Р1, Р2, Р3 пока неизвестны, причём Р1+ Р2 +Рз=1 Используя условие, получаем систему двух уравнений с тремя неизвестными
Поскольку Р1+ Р2 +Рз=1 и Рз=1- Р1- Р2, то система уравнений принимает вид
откуда Р1 =0,2, Р2 =0,3. Поэтому Р3 =1- Р1 - Р2 =0,5.
Итак, закон распределения случайной величины Х определяется таблицей
Пример 8. Дискретная случайная величина X может принимать только два значения х1 и х2, причем, x1,<x2. Известны вероятность р= 0,5, математическое ожидание М(Х) = 3,5 и дисперсия D(Х) = 0,25. Найти закон распределения дискретной случайной величины X. М(Х)= 0,5x1+ 0,5х2 = 3,5, откуда х1 +х2 =7. По формуле (2.5.12) находим
и учитывая условие х1 < х2, получаем, х1 = 3, х2 = 4. Следовательно, Р(Х = 3) = 0,5, Р(Х= 4) = 0,5.
В соответствии с формулой (2.5.13) найдем D(X)
Решение. С помощью формулы (2.4.7) находим математическое ожидание:
По формулам (2.5.13) и (2.5.16) соответственно получаем
Пример 11. случайная величина Х задана функцией распределения
Найти числовые характеристики случайной величины Х: М(Х), D(X), σ(X). Решение. Сначала найдем плотность распределения р(х) с помощью формулы (2.3.5). так как р(х)=F’(x), то
|

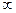 , +
, +  0. (2.5.3)
0. (2.5.3)
 (2.5.10)
(2.5.10)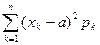 (2.5.10 a)
(2.5.10 a)
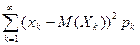 (2.5.12)
(2.5.12) (2.5.13)
(2.5.13) . (2.5.14)
. (2.5.14) (2.5.15)
(2.5.15) (2.5.16)
(2.5.16) .
.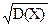 =1.
=1.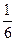
 ;
;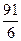 .
.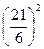 =
= 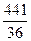 =
=  =
= 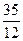 .
.
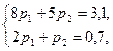
 ,
,


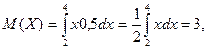 M(X)=3.
M(X)=3. , D(X)=1/3.
, D(X)=1/3. .
.
 .
.