МЕТОДИЧНІ ВКАЗІВКИ. 1. Вказівка шифру завдання
1. Вказівка шифру завдання. Варіант Я35 2. Представлення розрахункової схеми і початкових даних.
Рис. 5.1. Розрахункова схема На схемі показана система координат. Для осі z (відповідно для прогину w і нормального тиску q) позитивним вважається напрям вниз.
Таблиця 2. Початкові дані
Розрахункова схема містить 2чинники, кожний з яких вимагає розбиття пластини на ділянки: наявність проміжної опори на колі зміна характеру зовнішнього навантаження уздовж лінії Тому необхідно розглянути дві ділянки радіуса пластини:
при цьому точки кола У запропонованому прикладі приведене рішення варіанта Я35.
Рішення рівняння Софі Жермен
3. Формулювання задачі. Диференціальні рівняння відносно прогину пластини: I ділянка II ділянка Граничні умови: жорстке защемлення: вільний край: Рівність (5.4) відносно прогину виходить з (2.5) і (2.6):
Умови сполучення на границі ділянок
Остання рівність з урахуванням постійності жорсткості
4. Відшукання загального рішення. Послідовне інтегрування рівняння (5.1) приводить до наступних виразів:
у яких С1, С2, С3, С4 - невизначені константи. Аналогічно з (5.2) виходить:
5. Отримання системи рівнянь для пошуку констант. Константи інтегрування С1 - С8 визначаються із співвідношень (5.3), (5.5), (5.6) і (5.7):
(5.16)
Система лінійних відносно С1 - С8 рівнянь (5.16) може бути представлена в канонічній формі:
де { Х } = { С1 С2 С3 С4 С5 С6 С7 C8 } Т - вектор невідомих; [А] - матрицякоефіцієнтів розміру 8x8; { В}- вектор правих частин. Для вирішення СЛАР вигляду (5.17) методом виключення Гауса можна застосувати стандартну програму gauss.exe. При її виклику необхідно задати розмірність системи N, елементи матриці [А] і вектора {В}. Для системи (5.16) N = 8; значення компонент [А] і {В}приведені в табл.3. Можливо також скористатися програмним пакетом комп’ютерної алгебри Maple.
Таблиця 3. Коефіцієнти рівняння
6. Рішення СЛАР. В результаті рішення одержано: С1 = -9.40211·10-1; С2 = -1.0966; С3 = -1.3057·10-2; С4 = -4.1021·10-2; С5 = -4.6592; С6 = -3.4931;С7 = -2.2393·10-1; C8= -5.2967·10-1. 7. Запис виразів для шуканих величин. Підстановка знайдених констант в (5.11) і (5.15) з використанням формули (2.5) приводить до остаточних виразів прогину, перерізуючої сили і згинаючих моментів для двох ділянок пластини:
I ділянка a £ r £ b:
II ділянка b £ r £ c:
8. Графічне зображення результатів. Розподілення уздовж радіусу пластини прогину, перерізуючої сили, радіального і окружного згинаючих моментів показані відповідно на рис. 5.4 - 5.7
Рис. 5.4. Прогин пластини
Рис. 5.5. Перерізуюча сила
Рис. 5.6. Радіальний згинаючий момент
Рис. 5.7. Окружний згинаючий момент
9. Підрахунок напружень. Найбільші нормальні напруження: - радіальне - окружне Найбільше дотичне напруження
СПИСОК ЛІТЕРАТУРИ
1. Тимошенко СП., Войновский-Кригер С. Пластинки и оболочки. - М.:Физматгиз, 1963. - 635 с. 2. Самуль В.И. Основы теории упругости и пластичности. - М.: Высш. школа,1970. - 288с.
ЗМІСТ
Навчальне видання
Львов Геннадій Іванович Сукіасов Володимир Георгійович
Аналіз осесиметричного згину круглих та кільцевих плаcтин
Методичні вказівки до індивідуальних домашніх завдань з курсу «Теорія пластин та оболонок» для студентів спеціальності 8.080303 «Комп’ютерна механіка»
Укладачі: ЛЬВОВ Геннадій Іванович СУКІАСОВ Володимир Георгійович
Роботу до видання рекомендував С. К. Шелковий
Відповідальний за випуск Г. І. Львов
Редактор Л. А. Пустовойтова
План 2011 р., поз..
Підп. до друку Формат 60 Друк-ризографія. Гарнітура Таймс. Ум. друк. арк. 2,5. Обл.-вид. арк. 3,0. Наклад 50 прим. Зам. №. Ціна договірна
Друкарня НТУ «ХПІ». 61002, Харків, 2, вул. Фрунзе, 21
МЕТОДИЧНІ ВКАЗІВКИ
|


 ;
;
 (5.1)
(5.1) (5.2)
(5.2) (5.3)
(5.3) (5.4)
(5.4) (5.5)
(5.5) (5.6)
(5.6) :
: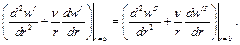 (5.7)
(5.7) (5.8)
(5.8)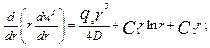 (5.9)
(5.9)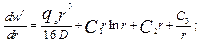 (5.10)
(5.10) (5.11)
(5.11) (5.12)
(5.12) (5.13)
(5.13) (5.14)
(5.14) (5.15)
(5.15)

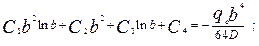


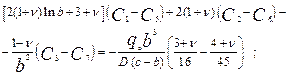

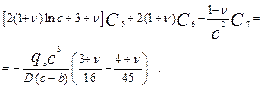
 (5.17)
(5.17)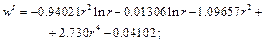
 (5.18)
(5.18)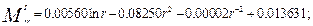


 (5.19)
(5.19)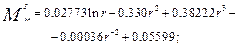






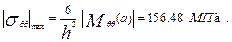
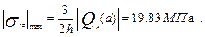
 841/16. Папір Morpa.
841/16. Папір Morpa.


