Интегрирование по частям
Интегрирование по частям обычно используется, если подынтегральная функция представляет произведение функций разных типов - степенная и показательная, степенная и тригонометрическая, обратная тригонометрическая функция и степенная, показательная и тригонометрическая и т.д. Интегрирование в этом случае производится с помощью формулы
где Укажем приоритеты выбора этой функции. 1. В первую очередь в качестве 2. При отсутствии этих функций в подынтегральном выражении в качестве Других приоритетов при выборе этой функции нет, задание Примеры. 1.
Билет Практические вопросы 1. Производная 2. Предел 3. Производная по направлению 4.Производные функции одной или нескольких переменных 5. Неопределенный или определенный интеграл 6. Математическое ожидание или дисперсия дискретно заданной случайной величины
Теоретические вопросы Методы Крамера или Гаусса. Линии на плоскости. Прямая на плоскости и в пространстве, ее уравнения, кривые второго порядка. Базис в 3-х мерном пространстве, представление вектора в базисе. Пределы, их свойства. Экстремумы функции одной переменной или наибольшее и наименьшее значения функции на отрезке Асимптоты кривой или правило Лопиталя. Формула Ньютона-Лейбница Интегрирование НИ и ОИ по частям и заменой переменной. Интегрирование простейших дробно рациональных функций. Интегралы
Представление правильной дробно рациональной функции в виде суммы простейших дробей. Универсальнапя тригонометрическая подстановка. Замена Основные формулы комбинаторики Определения вероятности случайного события Сумма или произведение случайных событий, их вероятность Математическое ожидание, дисперсия, их свойства, среднее квадратическое отклонение. Нормальный закон распределения, его параметры. Генеральная и выборочная совокупности, их точечные и интервальные оценки. Оценка генеральной совокупности по ее выборке. Смещенная и несмещенная оценки. Доверительный интервал. Коэффициент корреляции.
|

 ,
, функции одной переменной. При применении процедуры интегрирования по частям важен выбор функции
функции одной переменной. При применении процедуры интегрирования по частям важен выбор функции  .
.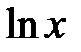 ,
, 
 .
. может быть выбрана находящаяся в числителе степенная функция с целым положительным показателем степени.
может быть выбрана находящаяся в числителе степенная функция с целым положительным показателем степени.
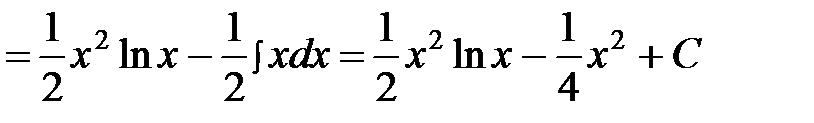 .
.
 .
. .
.


