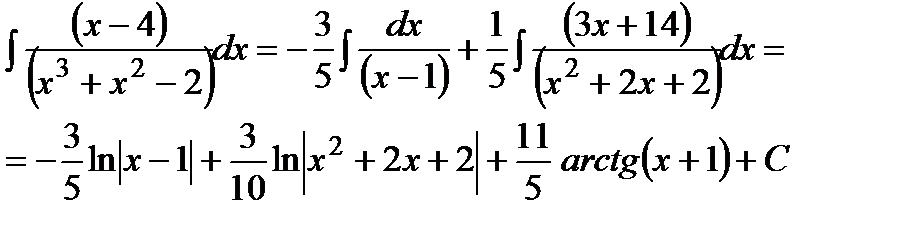Классы интегрируемых функций
Дробно рациональные функции
Интегрирование простейших дробно рациональных функций 1.
Интегрирование более сложных дробно рациональных функций Порядок действий 1. Установить, правильная дробно рациональная функция, или неправильная У правильной дробно рациональной функции
2. Поскольку интегрирование целой части не представляет трудностей, и если полученная правильная дробь простейшая, произвести интегрирование. 3. Если дробь правильная, но не простейшая, представить ее в виде суммы простейших дробей, для чего представить знаменатель дроби в виде произведения простейших выражений, используя формулу
Здесь Для определения коэффициентов Пример Поскольку
После приведения правой части к общему знаменателю, имеем
откуда следует
Это тождество приводит к системе уравнений
Решив систему, получаем В результате
|
.
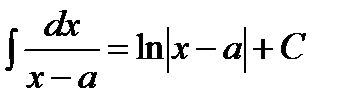. 2. 
.
.
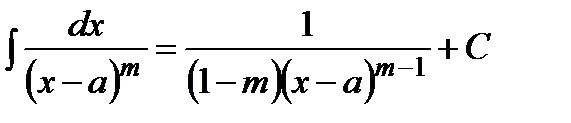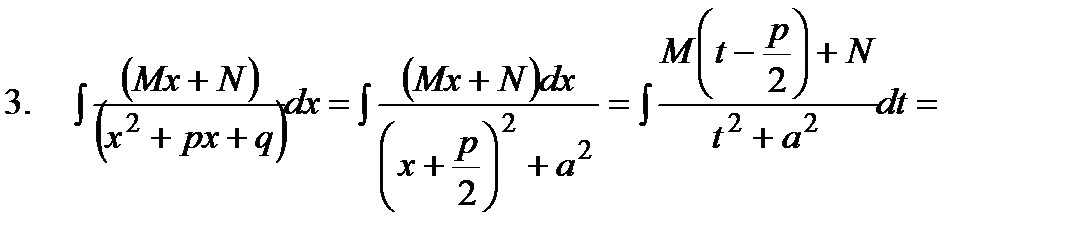
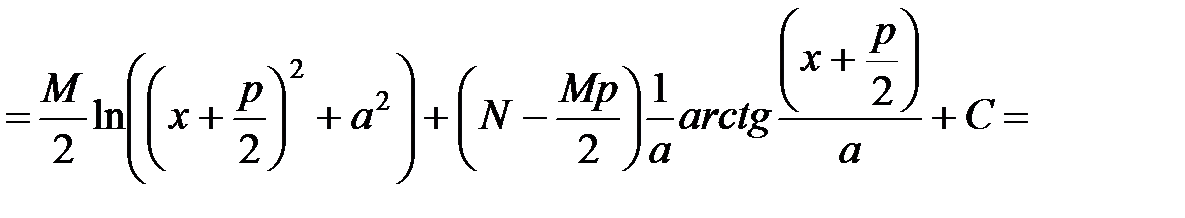
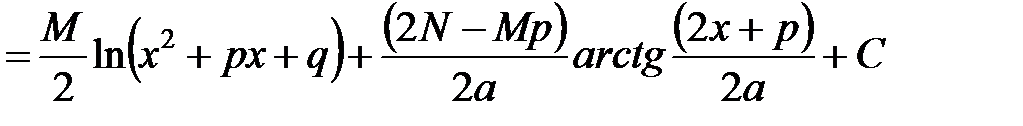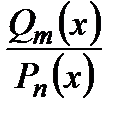
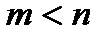, у неправильной
. Если дробь неправильная, представить ее в виде суммы целой части и правильной дроби (например, «делением углом»)
.
.
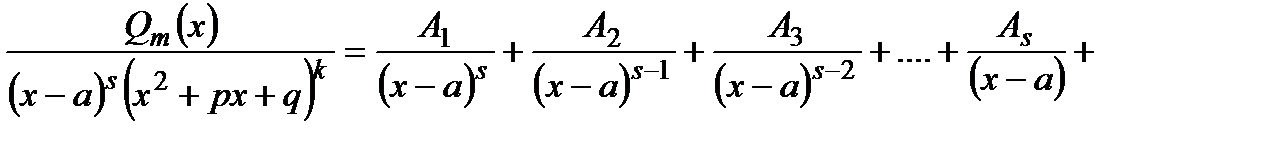
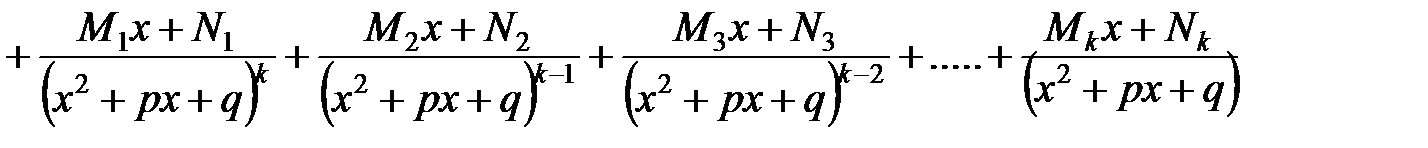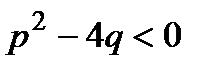необходимо привести правую часть к общему знаменателю, следя за тем, чтобы он совпадал со знаменателем левой дроби. Из равенства числителей дробей получить систему алгебраических уравнений относительно этих коэффициентов. Вычислить интегралы.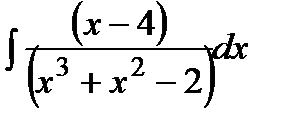
.
,
.
, 
, 
.
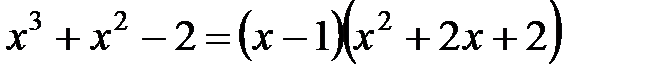
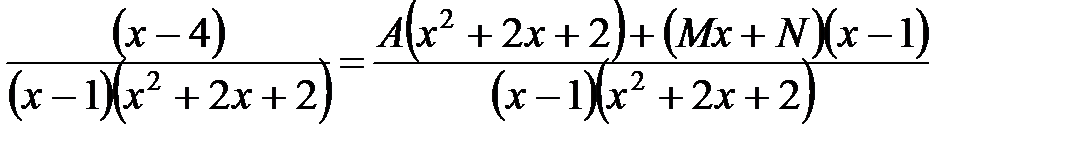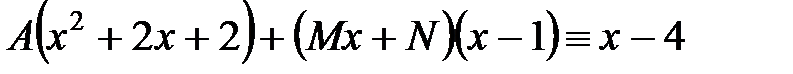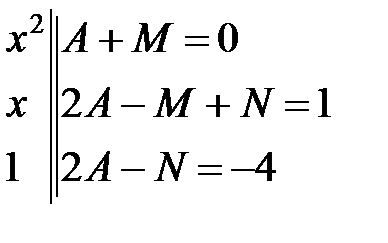
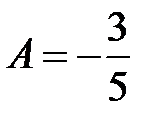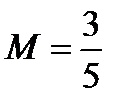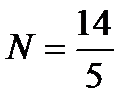