ЦЕНТРАЛЬНО-РАСТЯНУТЫЕ И ЦЕНТРАЛЬНО-СЖАТЫЕ ЭЛЕМЕНТЫ
5.1. Расчет на прочность элементов, подверженных центральному растяжению или сжатию силой N, кроме указанных в п. 5.2, следует выполнять по формуле Расчет на прочность сечений в местах крепления растянутых элементов из одиночных уголков, прикрепляемых одной полкой болтами, следует выполнять по формулам (5) и (6). При этом значение γс в формуле (6) должно приниматься по прил. 4* настоящих норм. 5.2. Расчет на прочность растянутых элементов конструкций из стали с отношением Ru / γu > Ry, эксплуатация которых возможна и после достижения металлом предела текучести, следует выполнять по формуле 5.3. Расчет на устойчивость сплошностенчатых элементов, подверженных центральному сжатию силой N, следует выполнять по формуле Значения φ следует определять по формулам при 0 < при 2,5 < при Численные значения φ; приведены в табл. 72. 5.4*. Стержни из одиночных уголков должны рассчитываться на центральное сжатие в соответствии с требованиями, изложенными в п. 5.3. При определении гибкости этих стержней радиус инерции сечения уголка i и расчетную длину lef следует принимать согласно пп. 6.1-6.7. При расчете поясов и элементов решетки пространственных конструкций из одиночных уголков следует выполнять требования п. 15.10* настоящих норм. 5.5. Сжатые элементы со сплошными стенками открытого П-образного сечения при λх < 3 λу, где λx и λy - расчетные гибкости элемента в плоскостях, перпендикулярных осям соответственно х - х и y - y (рис. 1), рекомендуется укреплять планками или решеткой, при этом должны быть выполнены требования пп. 5.6 и 5.8*. При отсутствии планок или решетки такие элементы помимо расчета по формуле (7) следует проверять на устойчивость при изгибно-крутильной форме потери устойчивости по формуле где φy - коэффициент продольного изгиба, вычисляемый согласно требованиям п. 5.3; c - коэффициент, определяемый по формуле где α; = αx / h - относительное расстояние между центром тяжести и центром изгиба. Здесь Jω - секториальный момент инерции сечения; bi и ti - соответственно ширина и толщина прямоугольных элементов, составляющих сечение. Для сечения, приведенного на рис. 1, а, значения где β; = b / h.
Рис. 1. П-образные сечения элементов а - открытое; б, в - укрепленные планками или решеткой Таблица 7
Обозначения, принятые в табл. 7: b - расстояние между осями ветвей; l - расстояние между центрами планок; λ - наибольшая гибкость всего стержня; λ1, λ2, λ3 - гибкости отдельных ветвей при изгибе их в плоскостях, перпендикулярных осям соответственно 1-1, 2-2 и 3-3, на участках между приваренными планками (в свету) или между центрами крайних болтов; А - площадь сечения всего стержня; Аd1 и Аd2 - площади сечений раскосов решеток (при крестовой решетке - двух раскосов), лежащих в плоскостях, перпендикулярных осям соответственно 1-1 и 2-2; Ad - площадь сечения раскоса решетки (при крестовой решетке - двух раскосов), лежащей в плоскости одной грани (для трехгранного равностороннего стержня); α1 и α2 - коэффициенты, определяемые по формуле где a, b, l - размеры, определяемые по рис. 2; n, n1, n2, n3 - коэффициенты, определяемые соответственно по формулам: здесь Jb1 и Jb3 - моменты инерции сечения ветвей относительно осей соответственно 1-1 и 3-3 (для сечений типов 1 и 3); Jb1 и Jb2 - то же, двух уголков относительно осей соответственно 1-1 и 2-2 (для сечения типа 2); Js - момент инерции сечения одной планки относительно собственной оси х-х (рис. 3); Js1 и Js2 - моменты инерции сечения одной из планок, лежащих в плоскостях, перпендикулярных осям соответственно 1-1 и 2-2 (для сечения типа 2). 5.6. Для составных сжатых стержней, ветви которых соединены планками или решетками, коэффициент φ; относительно свободной оси (перпендикулярной плоскости планок или решеток) должен определяться по формулам (8) - (10) с заменой в них В составных стержнях с решетками помимо расчета на устойчивость стержня в целом следует проверять устойчивость отдельных ветвей на участках между узлами. Гибкость отдельных ветвей λ1, λ2 и λ3 на участке между планками должка быть не более 40.
Рис. 2. Схема раскосной решетки
Рис. 3. Составной стержень на планках При наличии в одной из плоскостей сплошного листа вместо планок (рис. 1, б, в) гибкость ветви должна вычисляться по радиусу инерции полусечения относительно его оси, перпендикулярной плоскости планок. В составных стержнях с решетками гибкость отдельных ветвей между узлами должна быть не более 80 и не должна превышать приведенную гибкость λ ef стержня в целом. Допускается принимать более высокие значения гибкости ветвей, но не более 120, при условии, что расчет таких стержней выполнен по деформированной схеме. 5.7. Расчет составных элементов из уголков, швеллеров и т.п., соединенных вплотную или через прокладки, следует выполнять как сплошностенчатых при условии, что наибольшие расстояния на участках между приваренными планками (в свету) или между центрами крайних болтов не превышают: для сжатых элементов.... 40 i «растянутых «........... 80 i Здесь радиус инерции i уголка или швеллера следует принимать для тавровых или двутавровых сечений относительно оси, параллельной плоскости расположения прокладок, а для крестовых сечений - минимальный. При этом в пределах длины сжатого элемента следует ставить не менее двух прокладок. 5.8*. Расчет соединительных элементов (планок, решеток) сжатых составных стержней должен выполняться на условную поперечную силу Qfic, принимаемую постоянной по всей длине стержня и определяемую по формуле Qfic = 7,15 · 10-6 (2330 - E / Ry) N / φ;, (23)* где N - продольное усилие в составном стержне; φ; - коэффициент продольного изгиба, принимаемый для составного стержня в плоскости соединительных элементов. Условную поперечную силу Qfic следует распределять: при наличии только соединительных планок (решеток) поровну между планками (решетками), лежащими в плоскостях, перпендикулярных оси, относительно которой производится проверка устойчивости; при наличии сплошного листа и соединительных планок (решеток) - пополам между листом и планками (решетками), лежащими в плоскостях, параллельных листу; при расчете равносторонних трехгранных составных стержней условная поперечная сила, приходящаяся на систему соединительных элементов, расположенных в одной плоскости, должна приниматься равной 0,8 Qfic. 5.9. Расчет соединительных планок и их прикрепления (рис. 3) должен выполняться как расчет элементов безраскосных ферм на: силу F, срезывающую планку, по формуле F = Qsl / b; (24) момент М 1, изгибающий планку в ее плоскости, по формуле М 1 = Qsl / 2, (25) где Qs - условная поперечная сила, приходящаяся на планку одной грани. 5.10. Расчет соединительных решеток должен выполняться как расчет решеток ферм. При расчете перекрестных раскосов крестовой решетки с распорками (рис. 4) следует учитывать дополнительное усилие Nad, возникающее в каждом раскосе от обжатия поясов и определяемое по формуле где N - усилие в одной ветви стержня; А - площадь сечения одной ветви; Ad - площадь сечения одного раскоса; α; - коэффициент, определяемый по формуле α = al 2 / (a 3 + 2 b 3), (27) где а, l и b - размеры, указанные на рис. 4. 5.11. Расчет стержней, предназначенных для уменьшения расчетной длины сжатых элементов, должен выполняться на усилие, равное условной поперечной силе в основном сжатом элементе, определяемой по формуле (23)*.
|

 . (5)
. (5) . (6)
. (6) . (7)
. (7) ≤ 2,5
≤ 2,5 ; (8)
; (8) ; (9)
; (9) . (10)
. (10) , (11)
, (11) (12)
(12) ;
;  ;
; ;
;  ;
; ,
,  и α; должны определяться по формулам:
и α; должны определяться по формулам: ;
;  ;
;  , (13)
, (13)

 (14)
(14)
 (17)
(17)
 (20)
(20)

 (15)
(15)
 (18)
(18)
 (21)
(21)

 (16)
(16)
 (19)
(19)
 (22)
(22)
 ,
, ;
;  ;
;  ;
;  ,
, . Значение
. Значение 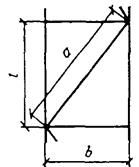

 , (26)
, (26)


