Модели динамики средних высот, диаметров и видовых чисел

 

Изменение средней высоты, диаметра и видового числа подчиняется несколько иным законам, чем прирост. С началом жизни дерева высота и диаметр начинают увеличиваться. Сначала медленно, но с некоторого периода наступает период бурного роста, а в приспевающих и спелых насаждениях рост деревьев замедляется. В конечном итоге рост по высоте прекращается, а по диаметру живое дерево растет постоянно. Поэтому требования к модели роста по высоте следующие.

-- Кривая должна начинаться в начале координат (точка 0).

-- Первоначальный рост идет медленно. Кривая имеет малый угол наклона к оси ОХ.

-- С определенного возраста идет ускорение роста.

-- После достижения возраста спелости рост сильно замедляется, а затем практически останавливается. Эта часть кривой становится почти параллельной оси абсцисс.

Наилучшим образом отмеченным условиям отвечает уравнение В.Н. Дракина и Д.И. Вуевского

Н_а = Н_max (1-е^-kа)^m, (16.10)

где Н_а - высота в возрасте а лет;

Н_max - максимально достижимая высота породы;

а - возраст;

k, m - коэффициенты.

Часто требуется описать (смоделировать) ход роста, когда начальный возраст древостоя равен 10 или 20 лет. Такое обычно бывает при составлении таблиц хода роста. В этом случае можно применить разные кривые. Наиболее простой из них является парабола 3-го порядка. Квадратную параболу (у = а₀ + а₁х + а₂х²), которую иногда тоже здесь используют, применять нежелательно из-за ее большой “жесткости”: она занижает или завышает граничные значения.

В настоящее время предложено много функций роста: несколько сотен. Для примера приведем уравнение Я.А. Юдицкого, являющееся одним из лучших

где а₁, а₂, а₃, t - параметры;

u - возраст.

е –основание натуральных логарифмов;

 

В ряде последних научных публикаций можно встретить утверждение, что функция Н = f(A) в конце жизни насаждения загибается книзу из-за усыхания крупных деревьев. Но результаты большинства исследований показывают, что такого не происходит.

Модель динамики среднего диаметра сходна с моделью изменения высоты. Отличие здесь в том, что правая ветвь кривой, которая выражает динамику диаметров, у живого дерева никогда не становится строго параллельной оси ОХ. Графики уравнений, описывающих зависимость высоты и диаметра от возраста, т. е. Н = f(A) и Д = f(A), которые взяты из т. х. р. В. Ф. Багинского и Ф. П. Моисеенко, приведены на рисунках 16.3 и 16.4.

 

Рисунок. 16.3. Динамика высот древостоев сосны

 

 

Рис. 16.4. Динамика диаметров древостоев березы

 

Закономерности изменения видового числа иные, чем диаметра и высоты. В лесной таксации обычно используют старое видовое число, которое находят по формуле:

,

 

где, V_ств _объём ствола

Vцил. - объем цилиндра с диаметром основания Дm.

В этом случае f будет меньше 1,0, когда Н ³ 1,3 м. Видовое число имеет высокую корреляцию с высотой. Как правило, связь f-Н выражается уравнением гиперболы:

Средний диаметр на величину видового числа существенного влияния не оказывает, т.к. оно поглощается корреляцией Н -Д. Более существенное значение в уравнении связи f=j (Н,Д) диаметр оказывает в молодняках, возрастом до 20-30 лет. Уравнения связи здесь бывают разные, но тоже типа гиперболы. Например,

 

 

График, показывающий срязь видового числа с высотой f = j(Н), имеет вид, показанный на рисунке 16.5.

f

 

 

H

 

Рисунок 16.5. График зависимости видового числа от высоты

 

Из рисунка 16.5 видно, что при увеличении высоты с минимальных значений до 15-25 м снижение f идет быстро, а после высоты 30-32м кривая становится почти параллельной оси абсцисс.

Изменение сумм площадей сечений (åg) и запасов (М) подчиняется примерно тем же законам, как и динамика средней высоты и диаметра. До определенного возраста эти величины увеличиваются медленно, затем идет бурный рост, а в конце жизни древостоя их приращение небольшое. В перестойных насаждениях åg и М могут даже уменьшаться, если идет распад древостоя и отпад превышает прирост на живых деревьях. Для математического выражения динамики åg и М от возраста можно использовать уравнение В.Н. Дракина и Д.И. Вуевского, параболу 3 порядка и др. В связи с высокой корреляцией åG—M обычно по уравнениям связи вычисляют динамику Н,G,F = f(A), а М определяют по формуле М= G H F. В практике лесоустройства запас обычно определяют по стандартной таблице сумм площадей сечений и запасов при полноте 1,0.
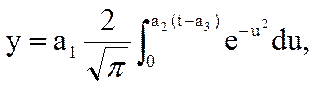