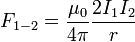Совокупность основных и производных единиц относящаяся к некоторой системе величин построенной в соответствии с принятыми принципами образует систему единиц.
Совокупность основных и производных единиц относящаяся к некоторой системе величин построенной в соответствии с принятыми принципами образует систему единиц. Для построения системы единиц следует, выбрав несколько основных, установить с помощью определяющих уравнений производные единицы всех остальных величин. Определяющие уравнения бывают двух типов: одни, по существу, представляют собой определение новой величин – такой, например, как ускорение или работа, другие выражают экспериментальную или теоретическую связь между исследуемыми величинами. К закономерностям этого типа относятся закон всемирного тяготения, закон Кулона и др. такое деление на «определения» и «законы» однако не играет существенной роли в определении новых единиц, поскольку в обоих случаях закономерности представляются в виде формул, связывающих данную величину с другими, для которых единиц установлены ранее. В выборе определяющих уравнений, как и в выборе размера основных единиц и числовых коэффициентов в определяющих уравнениях, не существует жестких ограничений. Вопрос, который требует большего рассмотрения – это вопрос о числе единиц. По этому вопросу существует две точки зрения. Согласно одной из них, число основных единиц задано нам природой и определяется характером тех явлений, которые подлежат рассмотрению. В качестве обоснования такого взгляда приводятся даже «философские» соображения о том, что каждое новое качество должно характеризоваться и измеряться новой основной единицей. При этом утверждается, что для описания всех явлений из области механики необходимо и достаточно иметь три единицы. При исследовании всех других явлений необходимо, кроме трех основных единиц, вводить по одной дополнительной, специфической для данной области единице физической величины. Сторонники другой точки зрения считают, что качества материального мира бесконечно многообразны, и если считать, что каждое качество характеризуется величиной, единица которой должна быть основной, то число таких единиц будет также бесконечно большим. Конечно, физические величины, отражающие реальные свойства окружающего нас мира, действительно бесконечно разнообразны и несводимы друг к другу. Однако единицы физических величин сами по себе не являются объектами природы, а представляют аппарат для ее изучения. Законы природы никак не изменят своего объективного характера при замене одних единиц другими. Поэтому основное требование, которое должно быть предъявлено к системе единиц, заключается в том, система должна быть, возможно, более удобной для практических целей. Число основных единиц тесно связано с числом коэффициентов, стоящих в выражениях физических законов и определений. Коэффициенты пропорциональности, подобные гравитационной и инерционной постоянным и зависящие от основных единиц и определяющих уравнений получили название фундаментальных постоянных. В этом их отличие от так называемых специфических постоянных, характеризующие различные свойства отдельных веществ (молярной массы, критической температуры. диэлектрической проницаемости и т. д.) Поскольку система единиц представляет своего рода аппарат, предназначенный для облегчения расчетов в науке и технике, она должна удовлетворять ряду практических требований. С этой точки зрения способы построения системы единиц и число основных единиц в известной степени ограничены. Слишком большое число основное число неизбежно связано с большим числом фундаментальных постоянных в физических формулах, что затрудняет их запоминание и удлиняет вычисления. Кроме того, потребовалась бы огромная работа по установлению эталонов всех основных единиц. точность, с которой устанавливались бы эти эталоны, была бы различной, вследствие чего отличались бы по точности и фундаментальные постоянные в формулах физических законов и определений. С другой стороны слишком малое число основных единиц ограничивает возможности построения произвольных единиц, так что многие из них окажутся либо слишком большими, либо слишком маленькими для практики. Заметим, что в настоящее время выражение «размер единиц, удобный для практики» стало несколько расплывчатым вследствие того, что диапазон размеров величин, встречающихся в науке и технике, чрезвычайно широк. Так, например, в ядерной физике приходится иметь дело с длинами порядка 10-15 м, а в астрономии порядка 1022-1026 м. Мощности электростанций превышают 109 Вт, а мощность сигнала, воспринимаемого радиолокационной станцией, достигает значений, меньших, чем 10-16 Вт. Исходя из этих соображений оказывается целесообразным строить системы единиц пригодные для различных областей физики, в которых число основных единиц было бы порядка пяти – семи. Поскольку формой существования всех видов материи является пространство – время, естественно включить в число основных единицы протяженности и времени. Хотя с точки зрения теории относительности длины отрезков и промежутков времени утратили свою абсолютность, поскольку они зависят от относительного движения систем отсчета, они сохранили свою объективность, подобно тому, как в обычной геометрии проекции отрезка на координатные оси, будучи относительными (т. е. зависящими от системы координат), тем не менее остаются объективными. Эти соображения позволяют нам без всяких оговорок включить в число основных единицы длины и времени. То же в полной мере относится и к третьей величине – массе, единицы которой обычно также выбираются в качестве основных. Чрезвычайно широкое распространение, которое имеет в науке, повседневной жизни температура, делает целесообразным ее выделение в число основных величин. В светотехнике, существенными являются величины, характеризующие субъективное восприятие света. Поэтому использование при определении единиц этих величин только энергетических параметров лишит их важнейшего качества – характеристики воздействия на наше зрение. Это потребовало введения специфических величин – силы света, светового потока, освещенности, яркости и др. Практические соображения потребовали включить в число величин, единицы которых принимаются за основные, одну из электрических или магнитных величин. После долгих дискуссий в качестве такой величины была принята сила тока. В настоящее время в физике и химии приходится иметь дело с такими величинами, как число единиц, концентрация частиц. Для определения и изменения числа частиц была введена особая величина, которой присвоено наименование «количество вещества». Таким образом, число основных единиц, на которых строятся системы единиц, достигло в настоящее время семи. Это единицы длины, массы, времени, температуры, силы тока, силы света и количества вещества. В течение длительного времени к числу основных величин относилось и количество теплоты, которое было позже исключено после установления эквивалентности понятий энергия и работа. При этом должны быть удовлетворены важные требования – возможность сохранения постоянства, размера основных единиц, их воспроизведения, а в случае утраты – и их восстановления и должна быть обеспечена возможно более высокая точность, с которой могут сравниться образцовые меры данной единицы, изготовленные в разных местах. Очень важно также иметь возможность сравнивать между собой результаты измерений, произведенных с использованием разных единиц. Для этого надо знать соотношение между единицами, применяемыми в разных странах. Осуществить это единство лучше всего, если попытаться связать основные единицы с величинами, встречающимися в природе. Первый шаг в этом направлении был сделан во времена Великой французской революции, когда специальная комиссия в составе крупнейших французских ученых конца VIII века (куда входил и Лаплас) предложила принять в качестве единицы длины одну десятимиллионную часть четверти дуги Парижского меридиана. В результате работы комиссии в 1799 году во Франции был введен «метр подлинный и окончательный», послуживший основой метрической системы. Прототипом метра явилась специально изготовленная линейка – платиново-иридиевый стержень, хранящийся в настоящее время в Национальном архиве Франции. Одновременно с метром была введена единица веса ‑ килограмм[3], определенная вначале как вес кубического дециметра воды при температуре ее наибольшей плотности 4 ºС. Подобно тому, как для метра была изготовлена образцовая линейка, так и для сохранения килограмма была изготовлена образцовая платиново-иридиевая гиря – прототип килограмма. Сплав платины и иридия был выбран как обладающий очень малым температурным коэффициентом объемного расширения. Для образования кратных и дольных единиц длины и веса (массы) была принята десятичная система, согласно которой все более и крупные единицы получаются умножением основной единицы на положительную или отрицательную степень десяти. Поэтому совокупность всех единиц, построенных таким образом, назвали десятичной системой мер. Метрическая десятичная система включала в себя и ряд производных единиц: единицу площади – квадратный метр, единицу объема – кубический метр и их кратные, и дольные единицы. В качестве единицы времени была узаконена секунда как 1/86 400 часть средних солнечных суток. Повышение точности измерений, связанное с развитием измерительной техники, позволило, однако, обнаружить, что между выбранными единицами и изготовленными для них прототипами существует хотя и небольшое, но вполне измеримое расхождение. Исключение составила лишь секунда, которая благодаря высокой точности астрономических измерений, оставалась практически неизменной и требовала лишь уточнения самой формулировки. В связи с этим встал вопрос о том, изготовить ли новые прототипы или примириться с имеющимся расхождением и принять в качестве законных единиц меры, определяемые существующими прототипами. Решено было зафиксировать прототипы как основные эталоны единиц этих величин. Таким образом, были установлены следующие основные единицы: ‑ единица длины – метр (м), определяемая как расстояние между осями штрихов, нанесенных на платино-иридиевой линейке, при 0 ºС; ‑ единица массы – килограмм (кг) – масса платино-иридиевой гири; ‑ единица времени – секунда, определяемая как 1/86400 часть средних солнечных суток. В 1960 году было заключено международное соглашение о выборе основных физических величин. Эти величины, а также производные физические величины составляют основу Международной системы единиц СИ. Существуют точные определения этих величин. Отметим, что на практике эти определения реализуются с конечной точностью, которая играетнемаловажную роль. Для этого используют разнообразные методы измерения, которые постоянно совершенствуются. Если обратиться к истории, то мы увидим, как, с одной стороны, возрастали требования к точности определения единиц физических величин, а с другой стороны, возникали принципиально новые способы их измерения. С помощью открытого в 1962 году эффекта Джозефсона были с большой точностью измерены некоторые атомные постоянные, что позволило разрешить противоречия, существовавшие на протяжении долгого времени в квантовой электродинамике. Исследователи стремились и стремятся связать основные физические величины с фундаментальными постоянными, которые можно в любое время измерить с хорошей воспроизводимостью, характерным примером является единица длины. Вначале метр определялся через длину окружности земного шара, с 1927 г. через длину красной линии кадмия, с 1960 г. – через излучение изотопа криптона 86Kr в оранжевой области видимого спектра (Метр – длина, равная 1650763,73 длины волны в вакууме излучения, соответствующего переходу между уровнями 2p10 и 5d5 атома криптона-86 по определению, принятому на XI Генеральной конференции по мерам и весам в 1960 году. Достижения лазерной техники и квантовой электроники, высокая точность, которой удалось достичь при измерении скорости света, позволили связать определение единицы длины – метра с единицей времени – секундой. В 1983 г. состоялась XVII Генеральная конференция по мерам и весам. На ней было установлено новое определение метра в связи с тем, что в настоящее время можно очень точно измерить скорость света: Метр равен длине пути, которую свет проходит в вакууме за 1/299 792 458 долю секунды. Скорость света в вакууме точно измерена. Она равна с = 299 792 458 м/с. Скорость света выбрана потому, что она является одной из фундаментальных постоянных природы. Измерить эталонную длину можно, определив время, за которое свет проходит этот отрезок. Развитие молекулярной и атомной радиоспектроскопии дало возможность достаточно точно связать единицы времени с периодом колебаний, соответствующим какой-либо определенной спектральной линии. Поэтому решением XIII Генеральной конференции по мерам и весам (1967 г.) было дано новое определение секунды, согласно которому секунда есть продолжительность 9 192 631 770 периодов излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия‑133 (изотопа цезия с массовым числом 133). Эталон секунды реализуется с помощью цезиевого излучения. Для определения такого промежутка времени необходимо уметь «сосчитать» 9 192 631 77 периодов атомного излучения. Таблица 1 – Основные величины и единицы измерения (Межгосударственный стандарт ГОСТ 8.417-2002 «Государственная система обеспечения единства измерений. Единицы величин» (введен в действие постановлением Госстандарта РФ от 4 февраля 2003 г. N 38-ст)
Заметим, что и единицу массы в принципе можно было бы определить не массой эталонной гири, а связать ее с массой какой-либо атомной частицы (например, нейтрона), этого не происходит потому, что точность определения атомных масс уступает точности измерения путем взвешивания. По вопросу включения в систему единицы, которая бы охватила все измерения в механике, электричестве и электромагнетизме на протяжении многих лет шли дискуссии. Предлагались единицы следующих величин: силы тока, разности потенциалов, сопротивления, электрической емкости, индуктивности, магнитного потока. Исходя из метрологических соображений, за основную единицу была выбрана единица силы тока – ампер. Взаимосвязь между электродинамикой и механикой позволила в 1948 г. на IX Генеральной конференции по мерам и весам определить единицу силы тока: Ампер равен силе постоянного электрического тока, который, протекая по двум параллельным прямолинейным бесконечно длинным проводникам с пренебрежительно малым круговым сечением, находящимся в вакууме на расстоянии 1 м друг от друга, вызывает на участке длиной 1 м силу взаимодействия между ними 2 × 10-7 Н. [4] Тем самым определяется численное значение другой фундаментальной постоянной физики: магнитной постоянной m0. Она равна m0 = 4 p ×10-7 Н/А2. Это соотношение в принципе эквивалентно приведенному выше определению ампера. Зная, что Основной термодинамической величиной является термодинамическая температура. Она измеряется в кельвинах. Поскольку для температуры существует значение абсолютного нуля, то для определения этой величины необходимо зафиксировать еще одну точку. В качестве нее выбрана тройная точка воды. Кельвин, единица термодинамической температуры, равен 1/273,16 части термодинамической температуры тройной точки воды (1967). Практическое измерение температуры проводят с помощью Международной практической температурной шкалы (IPTS ‑ 68/75), которая основана на целом ряде хорошо воспроизводимых фиксированных температурных точек. Количество вещества было введено в Международную систему единиц в качестве основной величины в 1971 г. В результате появилась возможность описывать количественные соотношения в химии и физической химии с помощью единиц СИ. Единица количества вещества определяется следующим образом: Моль представляет собой количество вещества в системе, содержащей столько же частиц, сколько атомов содержится в 0,012 килограмма изотопа углерода 12С. При использовании моля следует точно определить тип отдельной частицы. В качестве отдельной частицы могут выступать атомы, молекулы, ионы, электроны и другие частицы или группы частиц с точно заданными параметрами. Это число частиц называют числом Авогадро Na. Электромагнитное излучение описывается с помощью, так называемых, энергетических фотометрических величин, которые выражаются через первые три основные единицы. Если же нужно описать излучение через его воздействие на человеческий глаз, то для этого используют соответствующие редуцированные фотометрические (светотехнические) величины. Основной величиной при этом служит сила света, которая измеряется в канделах. В международном соглашении определена спектральная чувствительность человеческого глаза. Кривая спектральной чувствительности позволяет связать друг с другом энергетические фотометрические величины и светотехнические величины: мощность излучения и световой поток связаны между собой через так называемый фотометрический эквивалент излучения. В 1967 г. принято определение канделы, которое было основано на излучении света абсолютно черным телом при температуре затвердевания платины. К сожалению, это определение было не очень удобным, поскольку температура затвердевания платины несколько раз уточнялась, после чего всегда приходилось изменять фотометрический эквивалент излучения. Поэтому в 1979 г. было принято новое определение канделы. Кандела ‑ сила света источника, монохроматическое излучение которого частотой 540×1012 герц, излучаемое в определенном направлении в телесный угол величиной 1 стерадиан, имеет мощность 1/683 ватта. Частота 540 × 1012 Гц соответствует длине волны 555 нм, при которой человеческий глаз обладает максимальной чувствительностью. Все остальные величины называют производными величинами. Они определяются уравнениями, в которые входят основные физические величины. Производные физические величины можно представить через произведение основных величин Bi: G = Показатели степени bi это положительные или отрицательные целые числа. Наиболее важные из производных единиц имеют собственные имена и краткие обозначения.
Размерность физической величины Определим теперь понятие размерности физической величины. Аналогично существованию противоположных точек зрения на то, как должны строиться системы единиц (в частности, каково должно быть число основных единиц и какие единицы должны быть приняты за основные), имелись противоположные точки зрения на физическую сущность размерностей. Согласно одной из них, размерность выражает физическую связь между данной величиной и основными величинами системы. Противоположная точка зрения предполагает, что единственный смысл размерности – указание на то, как изменится единица данной величины при известном изменении единиц, принятых за основные. Изменение выбора основных единиц и определяющих уравнений может коренным образом изменить размерность. Очень четко эта точка зрения была выражена М. Планком, который писал: «… ясно, что размерность какой-либо величины не есть свойство, связанное с существом ее, но представляет просто некоторую условность, определяемую выбором системы измерений»[5]. Практически во всей литературе в настоящее время под размерностью понимается только обобщенное выражение зависимости единицы данной величины от основных единиц при принятом определяющем уравнении. Соотношение, показывающее, как изменяется единица какой-либо величины при изменении основных величин, называется размерностью этой величины. Наряду с использованием размерностей для перевода из одной системы в другую и установления соотношения между единицами, их применяют для проверки правильности формул, полученных в результате того или иного теоретического вывода. Неизменность размерности в рамках данной системы требует, чтобы размерности в левой и правой частях любого равенства, связывающего различные физические величины (или, точнее, числа, которыми эти величины выражаются), были одинаковы. В противном случае при переходе от одних величин к другим равенство бы нарушилось. Размерность показывает, как связана данная величина с основными физическими величинами, поэтому нет необходимости отдельно определять единицу измерения для каждой физической величины: они выражаются через произведение основных физических единиц с целыми показателями степени и численными множителями, равными 1. В Международной системе единиц СИ основным физическим величинам соответствуют основные единицы измерения: длина, масса, время, сила тока, температура, количество вещества и сила света. Для обозначения размерности произвольной физической величины используется ее буквенное обозначение, взятое в квадратные скобки. Так, например, символ [ v ] означает размерность скорости. Для размерностей основных величин используются специальные обозначения: для длины L, для массы M, для времени T. таким образом, обозначив длину буквой l, массу m и время буквой t, можно написать: [ l ] = L, [ m ] = M, [ t ] = T. В указанных обозначениях размерность произвольной физической величины в общем виде выражается в системе СИ как
В этом выражении все показатели степени ‑ целые числа, они могут быть как положительными, так и отрицательными. Если все они равны нулю, то величина G будет безразмерной. Так, например, размерность кинетической энергии Е кин имеет вид Е кин = dim Физическая величина и ее размерность ‑ это не одно и то же. Одинаковую размерность могут иметь совершенно разные по своей природе физические величины, например работа и вращающий момент или сила электрического тока и напряженность магнитного поля. Размерность не содержит информации о том, является ли данная физическая величина скаляром, вектором или тензором. Однако величина размерности важна для проверки правильности соотношений между физическими величинами. Поскольку физические законы не могут зависеть от выбора единиц входящих в них величин, размерности обеих частей уравнений, выражающих эти законы должны быть одинаковыми. Это условие может быть использовано, во-первых, для проверки правильности полученных физических соотношений и, во-вторых, для установления размерностей физических величин. Так, например, скорость определяется как На основании соотношения
Размерность силы
Аналогично устанавливаются размерности всех прочих величин.
[2] Катодные лучи — поток электронов, излучаемый катодом. Катодные лучи используются в телевизионных трубках, компьютерных мониторах, осциллографах, электронных микроскопах и радиолампах. В этих приборах катодные лучи распространяются в вакууме. Катодные лучи отклоняются магнитным и электрическим полем. С 1895 года Джозеф Джон Томсон в Кавендишской лаборатории Кембриджского университета начинает методическое количественное изучение отклонения катодных лучей в электрических и магнитных полях. Итоги этой работы были опубликованы в 1897 г. в октябрьском номере журнала «Philosophical Magazine». В своем опыте Томсон доказал, что все частицы, образующие катодные лучи, тождественны друг другу и входят в состав вещества. Суть опытов и гипотезу о существовании материи в состоянии ещё более тонкого дробления, чем атомы, Томсон изложил на вечернем заседании Королевского общества 29 апреля 1897 г. За это открытие Томсон в 1906 году получил Нобелевскую премию по физике. Опыт Томсона заключался в изучении пучков катодных лучей проходящих через систему параллельных металлических пластин, создававших электрическое поле и систем катушек, создававших магнитное поле. Обнаружено, что лучи отклонялись при действии отдельно обоих полей, а при определенном соотношении между ними пучки не изменяли прямой траектории. скорость движения частиц гораздо ниже скорости света ‑ таким образом было показано, что частицы должны обладать массой. Далее была выдвинуто предположение о наличии этих частиц в атомах и модель атома, впоследствии развитая в опытах Резерфорда. [3] По существу, килограмм является единицей массы, но во время его установления не делали различия между весом и массой. [4] В вакууме на расстоянии r друг от друга расположены два бесконечных параллельных проводника, в которых в одном направлении текут токи I 1 и I 2. Требуется найти силу, действующую на единицу длины проводника. Бесконечный проводник с током I 1 в точке на расстоянии r создаёт магнитное поле с индукцией:
По закону Ампера найдём силу, с которой первый проводник действует на второй:
По правилу буравчика, Модуль данной силы (r ‑ расстояние между проводниками):
Интегрируем, учитывая только проводник единичной длины (пределы l от 0 до 1):
[5] Планк М. Введение в теоретическую физику. Ссылка дана по книге Л. А. Сена «Единицы физических величин и их размерностей», М.: Наука, 1988.
|

 можно точно определить диэлектрическую постоянную e0, которую уже не нужно измерять экспериментально.
можно точно определить диэлектрическую постоянную e0, которую уже не нужно измерять экспериментально.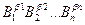 (1)
(1)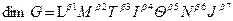
 (mv 2/2) = ML 2 T -2
(mv 2/2) = ML 2 T -2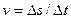 . Размерность
. Размерность  равна L, размерность
равна L, размерность 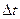 равна T. Размерность правой части написанного соотношения равна [s][t] = L/T = LT -1. Размерность левой части должна быть такой же. Следовательно, [ v ] = LT -1. написанное соотношение называется формулой размерности, а его правая часть – размерностью соответствующей величины, в данном случае скорости.
равна T. Размерность правой части написанного соотношения равна [s][t] = L/T = LT -1. Размерность левой части должна быть такой же. Следовательно, [ v ] = LT -1. написанное соотношение называется формулой размерности, а его правая часть – размерностью соответствующей величины, в данном случае скорости.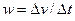 можно установить размерность ускорения:
можно установить размерность ускорения:
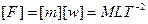
 (по закону Био ‑ Савара ‑ Лапласа).
(по закону Био ‑ Савара ‑ Лапласа).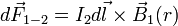
 направлена в сторону первого проводника (аналогично и для
направлена в сторону первого проводника (аналогично и для  , а значит, проводники притягиваются).
, а значит, проводники притягиваются).