Пример. 1. Биоэтика: междисциплинарные стратегии и приоритеты: учеб.-метод
1. Биоэтика: междисциплинарные стратегии и приоритеты: учеб.-метод. пособие/ Я.С. Яскевич, Б.Г.Юдин, С.Д. Денисов [и др.]; под ред. Я.С. Яскевич. – Минск: БГЭУ, 2007. – 225 с. 2. Летов, О.В. Биоэтика и современная медицина / РАН, ИНИОН. Центр гуманитарных науч.-информ. исслед. Отдел философии. – М., 2009. – 226 с. 3. Лопатин П.В. Биоэтика: Учебник /П.В. Лопатин О.В. Карташова. – 4-е изд., перераб. и доп. – М.: ГЭОТАР-Медиа, 2010. – 269 с. 4. Сергеев В. В. Биоэтика. Учебное пособие. – М.: ГЭОТАР-Медиа, 2010. – 240 с. 5. Силуянова И.В. Биоэтика в России: ценности и законы. – М.: РНИМУ им. Н.И.Пирогова, 2014. – 192с. 6. Силуянова И.В. Руководство по этико-правовым основам медицинской деятельности: Учебн. пособие / И.В. Силуянова. – М.: МЕДпресс-информ, 2008. – 224 с. 7. Тищенко П.Д. На гранях жизни и смерти: философские исследования оснований биоэтики. – СПб.: Изд. дом «Мiръ», 2011. – 328 с. 8. Хрусталев Ю.М. Введение в биомедицинскую этику: Уч. пособие для студентов мед. и фармацевт. вузов /Ю.М. Хрусталев – М.: ИП «Академия», 2010 – 221с. 9. Хрусталев Ю.М. От этики до биоэтики: учебник для вузов / Ю.М. Хрусталев. – Ростов н/Д: Феникс. 2010. – 446 с. 10. Швейцер А. Благоговение перед жизнью. – М., 1992. – 274с. 11. Швейцер А. Культура и этика. – М., 1973. – С. 305-308, 314 – 316.
Клаузальная форма. Клаузы Хорна. Формулы в виде Хорна имеют вид:
z и pi – предикаты или их отрицания
где pi- посылки, Такое правило называют правилом вывода или Хорна, или клаузами Хорна. Если клаузы выглядят так: Если клаузы выглядят так:
Пример. Пусть имеются предикаты: М(x,y)=”x – мать y” O(x,y)=”x – отец y” Дед(x,y)=”x – дед y” Запишем правила Хорна. К1. Дед(x,y)← O(x,z), М(z,y) К2. Дед(x,y)← O(x,z), O(z,y)
Любую логическую формулу можно преобразовать к одному или нескольким правилам Хорна с помощью следующей последовательности действий: 1. Исключение знака импликации → и эквивалентности ↔. A ↔ B = (A → B) Ù (A → B) A → B = ~A Ú B
2. Продвижение знака отрицания до атома ~(A Ú B) = ~A Ù ~B ~(A Ù B) = ~A Ú ~B ~(~A) = A ~("x)A(x) = ($x)~A(x) ~($x)A(x) =("x)~A(x)
3. Стандартизация переменных (переименование). Связанные переменные в случае, если они встречаются в других частях формул, переименовываются. $y("x P(x,y) Ú $x Q(x,y)) $y("z P(z,y) Ú $x Q(x,y))
4. Вынесение кванторов, т.е. получение предваренной формы. $y "z $x (P(z,y) Ú Q(x,y))
5. Избавление от кванторов существования. Если квантор существования стоит на первом месте, то он отбрасывается, а вхождение его переменной заменяется на константу, которой в формуле раньше не было. "z $x (P(z,a) Ú Q(x,a))
Если квантор существования стоит не на первом месте, то он отбрасывается и вхождение переменной заменяется на функцию от (k-1) переменной соответственно предшествующим кванторам всеобщности. "z (P(z,a) Ú Q(f(z),a))
При этом функциональный символ должен отличаться от всех имеющихся функциональных символов в формуле.
6. Кванторы всеобщности отбрасываются.
7. Получение конъюнктивной нормальной формы, т.е. формула должна быть преобразована в конъюнкцию дизъюнктов. A Ù (B Ú C) = (A Ù B) Ú (A Ù C) A Ù (B Ù C) = A Ù B Ù C A Ú (B Ú C) = A Ú B Ú C A1 Ú A2 Ú A3 Ú(B1 Ù B2 Ù B3)=(A1 Ú A2 Ú A3 ÚB1) Ù (A1 Ú A2 Ú A3 ÚB2) Ù (A1 Ú A2 Ú A3 ÚB3)
8. Запись в виде множества дизъюнктов S={D1, D2, …, DN}
9. Каждый дизъюнкт записывается в виде одного правила Хорна ~A Ú B=A → B ~A Ú ~B Ú C = C←A&B
|

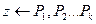
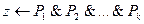 ,
,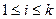 , а z – заключение
, а z – заключение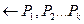 , то это заведомая ложь.
, то это заведомая ложь.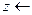 , то это факт.
, то это факт.


