ТЕОРЕТИЧЕСКАЯ ЧАСТЬ. Математические уравнения, описывающие основные закономерности движения жидкостей и газов не позволяют получить результаты для подавляющего большинства случаев
Математические уравнения, описывающие основные закономерности движения жидкостей и газов не позволяют получить результаты для подавляющего большинства случаев важных в практике, поэтому эксперимент в механике жидкостей и газов иногда может быть единственным доступным способом изучения гидродинамических явлений. Одним из основных методов эмпирического исследования гидродинамических процессов является их моделирование в лабораторных условиях, где как правило, исследуемые явления воспроизводятся на модели в совершенно другом масштабе, чем в натуральных условиях. Основой переноса результатов моделирования на натуральные условия является теория подобия. В основе теории подобия гидродинамических явлений лежат общие условия механического подобия. Явления считаются механически подобными, если в них: - одинаково отношение всех геометрических элементов – размеров. расстояний. углов. перемещений и т.п.; - одинаково отношение кинематических параметров в сходственных точках; - одинаково соотношение сил, действующих в сходственных точках и соответственных направлениях. Связь между любыми соответствующими геометрическими параметрами натурального и модельного потоков имеют вид:
где индекс “н” – относится к геометрическим размерам натурального потока; индекс “м” – обозначает размеры модели;
подобия. Кинематическое подобие состоит в том, что в любых сходственных точках отношение скоростей и проекций скоростей одинаково и равно масштабу скоростей
Теоретический анализ показывает, что из условия кинематического подобия автоматически следует геометрическое подобие линий тока, а для установившегося потока это условие означает и подобие траекторий. Динамическое подобие состоит в том, что все силы одинаковой природы и их проекции, действующие на любую пару сходственных элементов, отличаются друг от друга в натуральном потоке модели постоянным масштабом
Кинематическое и динамическое подобие могут иметь место только при наличии геометрического подобия. Теория подобия показывает, что все гидродинамически подобные потоки можно описать абсолютно одинаковыми уравнениями и зависимостями, для приведения математического описания к единой форме все геометрические, кинематические и динамические параметры выражают в относительных единицах. Для этого в качестве масштаба измерения в каждом из потоков выбирается некоторый характерный размер ℓ0, скорость υ0, время t0 и т.д. В гидродинамически подобных потоках, где все безразмерные параметры одинаковы, соответственно и все уравнения, представленные в безразмерном виде должны быть одинаковы. Рассмотрим подробнее динамическое подобие. Движение частиц жидкости, как известно, определяется силами, действующими внутри нее: Fоб – объемными силами (сила тяжести, подъемная сила); Fд – поверхностная сила давления; Fин – сила инерции. Пренебрегая силами поверхностного натяжения, составим уравнение, выражающее принцип Д’Аламбера для двух подобно перемещающихся элементарных объемов
Разделим обе части уравнения (4) на Ринτ 
Из постулата Ньютона, касательные напряжения, действующие в жидкости равны
тогда сила внутреннего трения (вязкости) при движении жидкости
где соприкосновения двух слоев, м2;
друга;
Сила инерции по закону Ньютона
массу элементарного объема
ускорение, как известно,
Правую часть уравнения (9) разделим и умножим нa
 и и 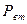 , найдем их отношение: , найдем их отношение:
т.к.
Данный безразмерный комплекс представляет собой критерий Рейнольдса, физический смысл которого указывает на отношение сил инерции в потоке жидкости к силам вязкости. Исходя из того, что
где
заменим отношение где
Безразмерный комплекс Приняв в качестве действующих в элементарном объеме
найдем отношение
Безразмерный комплекс
Полученные критерии Следует заметить, что все безразмерные комплексы или числа подобия можно разделить на два вида: - определяемые – это числа, в которые входят искомые переменные; - определяющие – это числа, целиком составленные из независимых переменных и постоянных величин, входящих в условие однозначности.  , ,  , ,  и величина давления Р. Они будут определяемыми величинами. К числу определяющих безразмерных величин в данном случае можно отнести независимые переменные x, y, z, t и безразмерные комплексы, выраженные числами подобия и величина давления Р. Они будут определяемыми величинами. К числу определяющих безразмерных величин в данном случае можно отнести независимые переменные x, y, z, t и безразмерные комплексы, выраженные числами подобия  , ,  и и  . .
Решение гидродинамических задач аналитическим путем или в результате обобщения экспериментальных данных сводится к установлению функциональных зависимостей определяемых параметров от определяющих.
Уравнения вида (18) называются уравнениями подобия.
Теория подобия
При моделировании изучение процесса в образце заменяется исследованием на модели. Условие моделирования, т.е. условие, которым должны удовлетворять модель и протекающий в ней процесс дает теория подобия. Теория подобия основана на трех теоремах составляющих ее суть: 1. Подобные процессы должны быть качественно одинаковыми, т.е. они должны иметь одинаковую физическую природу и описываться одинаковыми по форме записи дифференциальными уравнениями. 2. Должны соблюдаться условия однозначности, т.е. граничные и начальные условия должны быть одинаковы во всем, кроме числовых значений размерных постоянных. Условия однозначности для стационарных процессов состоят из: a) геометрических условий, полностью характеризующих форму и размеры канала, в котором происходит движение жидкости; b) физических условий, характеризующих физические свойства рассматриваемой сплошной среды; c) граничных условий, характеризующих особенности движения на границах потока. 3. Одноименные определяющие безразмерные переменные подобных процессов должны иметь одинаковые числовые значения. Обработка данных в виде критериальных уравнений позволяет получить результаты в более универсальной форме обобщения. Изучение моделирования в данной работе проводится на лабораторном стенде (рис.1), который включает в себя элементы дымового тракта современной металлургической печи. Важнейшей характеристикой металлургических печей является их тепловая мощность, определяемая количеством полезно усвоенного тепла рабочем пространстве, которое ограничено пропускной способностью системы, отводящей продукты горения в воздухонагреватели, каналы, борова и дымовую трубу. Оценить пропускную способность отводящей системы печи можно путем исследования модели, используя ее аэродинамическую характеристику – эквивалентное отверстие. независимых
В механике газов известна аэродинамическая характеристика печей, называемая эквивалентным отверстием:
где V – количество газов, м3/сек;
трение, мм вод. ст.; g, В наших опытах плотность воздуха принимаем Уравнение (19) можно преобразовать:
где А = 4,04. Из уравнения (20) видно, что эквивалентное отверстие связывает количество движущихся газов и потерю давления на преодоление местных сопротивлений (включая трение) при движении этого же количества газов. Как известно, эквивалентное отверстие является единственной характеристикой движущихся газов в системе печей, поэтому использование понятия об эквивалентном отверстии позволяет быстро производить различного рода расчеты механики газов. В работе воспользуемся понятием об эквивалентном отверстии для определения количества продуктов горения, из уравнения (20)
предварительно вычислив величину эквивалентного отверстия по результатам исследования модели и воспользовавшись соотношениями теории подобия. Согласно теории подобия отношение линейных размеров образца и модели, называемое масштабом модели, определяют:
где
Отношение сходственных площадей образца и модели составляет квадрат масштаба
Отношение сходственных объемов образца и модели равно масштабу в кубе
Поскольку эквивалентное отверстие имеет физический смысл отверстия определенной площади, через которое вытекает количество газов, равное количеству удаляемых из печи продуктов горения под давлением, равным сумме потерь на местные сопротивления и трение – можно вычислить с помощью масштаба величину эквивалентного отверстия для печи
где Ф – эквивалентное отверстие образца (печи), м2;
М – геометрический масштаб модели. В нашем случае М 1:20, т.к. установка, схема которой показана на рис.1 выполнена в одну двадцатую натуральной величины. Подставив Ф из уравнения (24) и уравнение (20) получим:
Из уравнения (25) видно, что для решения поставленной задачи требуется определить эквивалентное отверстие модели В нашем случае АМ2 = 1616, поэтому уравнение (25) примет вид:
Уравнение (26) в дальнейшем используем для составления характеристики пропускной способности исследуемой печи при различных значениях
|

 , (1)
, (1) - линейный масштаб или константа геометрического
- линейный масштаб или константа геометрического , т.е. выполняется условие
, т.е. выполняется условие . (2)
. (2) , т.е. должны действовать одинаковые по природе силы и при этом выполняются условия
, т.е. должны действовать одинаковые по природе силы и при этом выполняются условия . (3)
. (3) (4)
(4) , Па (Н/м2) (5)
, Па (Н/м2) (5) , (6)
, (6)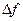 - элементарная площадка поверхности
- элементарная площадка поверхности - коэффициент динамической вязкости, Паּс;
- коэффициент динамической вязкости, Паּс;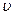 - скорость перемещения слоев относительно друг
- скорость перемещения слоев относительно друг - расстояние площадки
- расстояние площадки  (7)
(7) можно выразить
можно выразить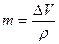 , кг (8)
, кг (8) , м/с2 (9)
, м/с2 (9)

 , (10)
, (10) (линейный размер),
(линейный размер),  (коэффициент кинематической вязкости), то уравнение (10) можно преобразовать
(коэффициент кинематической вязкости), то уравнение (10) можно преобразовать , (11)
, (11) , (12)
, (12) - давление на площадке
- давление на площадке  (13)
(13) его конечным значением
его конечным значением  ,
, - линейный размер
- линейный размер , (14)
, (14) представляет собой критерий Эйлера, физический смысл которого определяется как отношение сил нормального давления к силам инерции.
представляет собой критерий Эйлера, физический смысл которого определяется как отношение сил нормального давления к силам инерции. , (15)
, (15)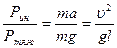 , (16)
, (16) представляет собой критерий Фруда, физический смысл которого определяется как отношение сил инерции к силам тяжести
представляет собой критерий Фруда, физический смысл которого определяется как отношение сил инерции к силам тяжести , (17)
, (17)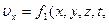



 (19)
(19) - сумма потерь давлений на местные сопротивления и
- сумма потерь давлений на местные сопротивления и - соответственно ускорение сил тяжести и плотность газов, м/сек2, кг/м3.
- соответственно ускорение сил тяжести и плотность газов, м/сек2, кг/м3. , (20)
, (20)
 , (21)
, (21) - линейные размеры образца;
- линейные размеры образца; - линейные размеры модели.
- линейные размеры модели. . (22)
. (22) . (23)
. (23) , (24)
, (24) - эквивалентное отверстие модели, м2;
- эквивалентное отверстие модели, м2; , м3/сек. (25)
, м3/сек. (25)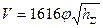 , м3/сек. (26)
, м3/сек. (26)


