ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ ОТВЕРСТИЕ И НАСАДКИ
Современная гидравлическая аппаратура работает при значительных рабочих давлениях. Она имеет большое количество, дросселей, выполняющих ответственные функции и в значительной степени влияющих на характеристику аппаратуры. Мы уже отмечали, что истечение из отверстия в тонкой стенке играет большую роль в гидравлике ЖРД. Дроссельные шайбы, жиклеры, струйные форсунки часто выполняются как круглые отверстия в тонкой стенке. Часто эти устройства работают в переходной области между ламинарным и турбулентным режимами, причем смена режима может проходить как слева на право, так и справа на лево, что вызывает динамику переходной области в отношении числа Рейнольдса. Из-за сложности физических процессов, происходящих в жидкости при ее протекании через дросселирующие элементы в переходной и турбулентной областях, коэффициент местного сопротивления данного элемента гидравлической магистрали не может быть определен теоретически. Он находится опытным путем. Рассмотрим истечение жидкости через круглое отверстие в тонкой стенке (рис. 6). Наблюдается сжатие струи вследствие сопротивления изгибу отдельных струек жидкости на входе в отверстие. В стабилизированном потоке изгиб струек совершается постепенно. Крайние струйки придают струе коноидальную форму и обусловливают сжатие струи на выходе из отверстия. У круглых отверстий считают наиболее сжатое (наименьшее по площади) сечение, отстоящее примерно на половину диаметра от входа потока в отверстие. После наибольшего сжатия струя расширяется. Для анализа истечения в данных условиях наибольший интерес представляет сжатое сечение. Так как струя истекает в среду с противодавлением Р2, то давление в сжатом сечении Рс равно Р2. Скорость в сжатом сечении (в сечении С) будет меньше теоретической (максимально возможной) скорости в силу присущих реальным гидравлическим процессам потерь и будет равна
Заменить в этой формуле W на WС где φ = WС/WТ – коэффициент скорости; WС – действительная скорость истечения в сжатом сечении струи; WТ – теоретическая скорость истечения в сжатом сечении струи. Объемный расход жидкости через отверстие в тонкой стенке может быть найден по параметрам сжатого сечения как Q = FСWС, здесь FС – площадь струи в сжатом сечении. Введя характеристику сжатия струи ε = FС/F, находим с учетом (27)
где μ = φε – коэффициент расхода отверстия в тонкой стенке, определяемый сжатием струи, характеризуемом коэффициентом ε, и неравномерностью распределения скоростей в расчетном сжатом сечении струи, характеризуемом коэффициентом скорости φ На величину коэффициентов φ и ε оказывают влияние факторы, характеризуемые числами (критериями) Рейнольдса, Фруда, Вебера. В практических случаях при истечении через отверстия влияниями чисел Fr и Wе можно пренебречь и считать коэффициенты φ и ε, а следовательно, и коэффициент расхода μ функциями только числа Rе. На рис. 7 Показаны экспериментальные зависимости названных выше коэффициентов от числа Рейнольдса. Из этих данных следует, что в широком диапазоне чисел Rе = 104…2·106 коэффициент расхода для круглых отверстий изменяется незначительно. Поэтому для конкретного отверстия его в этом диапазоне изменения числа Рейнольдса можно считать величиной постоянной. Таким образом, можно весь диапазон изменения чисел Rе разбить на две области: область, где μ = f(Rе) и квадратичную область (в которой потери напора зависят от расхода во второй степени - в квадрате), где μ = const. В цилиндрическом протяженном отверстии (этот тип отверстия называют насадком) имеет место более сложное течение жидкости. На рисунке 8 показана схема истечения жидкости через цилиндрическое отверстие, имеющее протяженность (через насадок). В этом случае струя, расширяясь, замыкается на стенку и образуется кольцевая изолированная полость, в которой устанавливается давление РС. Эта ситуация от рассмотренного выше случая отличается только тем, что Р2 в формуле (27) необходимо заменить на РС. Тогда расход жидкости через цилиндрическое отверстие определится по формуле В насадке так же, как и в отверстии в тонкой стенке (далее просто в отверстии), струя на входе имеет коноидальную форму и ее течение до сжатого сечения не отличается от такового в отверстии, т.е. эти процессы идентичны. Поэтому нет основания предполагать, чтобы коэффициенты сжатия и скорости, а следовательно, и коэффициент расхода μ отверстия и насадка отличались между собой. Для этих элементов гидравлических трактов в квадратичной области можно принять одинаковые коэффициенты: φ = 0,97, ε = 0,64, μ = φε = 0,62. Таким образом, остается единственное различие в расходных характеристиках отверстия и насадка – это неравенство РС и Р2. Для определения РС через известные величины параметров на входе и выходе цилиндрического отверстия составим уравнение Бернулли для сечений 1, где можно принять скорость, равную нулю, и С, т.е. максимально сжатого сечения:
где ξ – коэффициент сопротивления, соответствующий суживающемуся участку струи. Определим скорость на выходе из насадка W2:
где φ2 – коэффициент скорости, соответствующий выходному сечению. Из уравнения неразрывности W2F2 = WСFС находим WС = W2 Р-РС = Учитывая, что в выражении (32) перед разностью давлений все члены постоянные, обозначим его через ν. Тогда, решая уравнение (32) относительно РС, находим РС = Р2ν – Р(ν – 1) (33) или т.е. коэффициент ν есть отношение действительного перепада давления на расчетном сжатом сечении струи к общему перепаду давления на отверстии. Таким образом, коэффициент ν является характеристикой отверстия. По уравнению (33) в зависимости от Р могут быть получены положительные и отрицательные значения РС. В реальных условиях РС не может быть ниже давления упругости (давления насыщенных паров жидкости при ее температуре Рп), т.е. РС ограничивается кавитационными явлениями. Расход жидкости через насадок определяется уравнением расхода (29). Подставим в это уравнение разность Р-РС из выражения (34), получим
тогда скорость потока в сжатом сечении струи будет
Сравнение уравнений расхода для отверстия и насадка показывает, что расход через насадок увеличивается по сравнению с расходом через отверстие в тонкой стенке в ν раз из-за возрастания скорости потока в сжатом сечении струи. Следует отметить (обратить внимание), что при истечении жидкости через насадок кольцевая полость существует не всегда. При некоторых условиях происходит разрушение этой полости или, как принято называть в гидродинамике, происходит срыв течения. Разрушение кольцевой полости приводит к тому, что среда с противодавлением Р2 входит внутрь отверстия, перепад давления на сжатом сечении струи резко уменьшается, что влечет за собой снижение скорости струи и, соответственно, снижение расхода. Уравнение (35) вырождается в уравнение (28). Рассмотрим условия возникновения, существования и разрушения кольцевой изолированной полости. Кольцевая изолированная полость уже возникает при небольшом перепаде давления: Δ= Р-Р2. Возникшая кольцевая полость сохраняется в дальнейшем благодаря равновесию сил, действующих на частицы жидкости, находящиеся на границе плоскости в расширяющейся части потока (демонстрируется, воспроизводится, на доске рисунок). Это скоростная составляющая силы потока и сила, обусловленная разностью давлений Р2 – РС. Разрушение кольцевой изолированной полости и связанное с этим изменение закона истечения жидкости может происходить только при истечении в газовую среду. При истечении в жидкость полость сохраняется и противодавление Р2 не проникает внутрь насадка, тем самым обеспечивается и сохраняется фактор Р2 > РС. При условиях процесса истечения, формирующих минимальное значение давления РС, и способствующих росту скорости потока, полость деформируется, достигает границ насадка, -и среда с противодавлением Р2 входит внутрь насадка (рис. 9 и рис. 10). Как уже отмечалось (обращалось внимание) устойчивость режима истечения в насадке зависит от его относительной длины ℓ/d. Если длина насадка мала, то изолированная полость регулярно не образуется, а имеет место срывной режим течения. При достаточной длине насадка за счет образования изолированной полости (ее часто называют застойной областью) режим течения становится устойчивым. Этот геометрический критерий оценивается как ℓ/d > 1.5 (рис. 11 и рис. 12).
ЛЕКЦИЯ 3(ПРОДОЛЖИТЕЛЬНОСТЬ 2 ЧАСА, ОДНА ПАРА)
Тема 1. Кавитация. Кавитационные режимы. Число кавитации Тема 2. Кавитация в местных гидравлических сопротивлениях
ЛИТЕРАТУРА 1. Арзуманов Э. С. Кавитация в местных гидравлических сопротивлениях. М: Энергия, 1978г. 2. Сточек Н. П., Шапиро А. С. Гидравлика жидкостных ракетных двигателей. М: Машиностроение, 1978. 3. Некрасов Б. Б. Гидравлика и ее применение на летательных аппаратах. М: Машиностроение, 1967
РИСУНКИ Рис. 1. Диаграмма Р-V Рис. 2. Скорость роста сферического кавитационного пузырька в и деальной и вязкой жидкости (рис. 1-3 по Э. С. Арзуманову) Рис. 3. Схема течения жидкости в простейшем местном сопротивлении (рис. 1-7 по Э. С. Арзуманову) Рис. 4. Зависимость между ξу и χ (рис. 3-28 по Э. С. Арзуманову) Рис. 5. Зависимость ξу от χ (рис. 5-24 по Э. С. Арзуманову) Рис. 6. Зависимость χкр от ξу (рис. 5-24 по Э. С. Арзуманову) Рис. 7. Зависимость χкр от ξу для аммиака (рис. 5-25 по Э. С. Арзуманову) Рис. 8. Схема трубки для демонстрации кавитации (рис. 42 по Б. Б. Некрасову) Рис. 9. Зависимость расхода через кавитационную трубку (рис. 44 по Б. Б. Некрасову) Рис10. Обобщенная зависимость расхода через кавитационную трубку (рис. 44 по Б. Б. Некрасову
КАВИТАЦИЯ. КАВИТАЦИОННЫЕ РЕЖИМЫ. ЧИСЛО КАВИТАЦИИ
Под кавитацией понимают появление в капельной жидкости областей (каверн), заполненных парами или газами, выделившимися из жидкости. Обычно явление кавитации происходит в тех случаях, когда абсолютное давление в какой-либо области капельной жидкости упадет ниже некоторого критического значения давления Ркав, при котором возникают разрывы сплошности жидкости и образуются каверны, заполненные паром или газом (или парогазовой смесью). Часто давление Ркав совпадает с давлением Рн насыщенного пара жидкости при данной температуре и явление кавитации может трактоваться как явление вскипания жидкости, обусловленное понижением давления или повышением температуры. Кавитация может возникнуть как в покоящейся жидкости, так и в движущейся. При этом она может наблюдаться как в объеме, удаленном от поверхности, так и в областях на твердых границах. Если понижение давления, при котором образуются разрывы сплошности, происходит вследствие возникновения больших местных скоростей в потоке движущейся жидкости, кавитацию называют гидродинамической. Различают еще кавитацию акустического происхождения, когда причиной разрыва сплошности является переменное давление, создаваемое в объеме жидкости источником колебаний (в основном источником ультразвуковых колебаний). Кавитационные явления, происходящие в местных гидравлических сопротивлениях, относятся к гидродинамической кавитации. Кавитация в гидродинамических системах и устройствах (стендовых агрегатах) возникает прежде всего в тех местах, где поток претерпевает местное сужение с последующим расширением, например, в запорных и регулирующих органах, отверстиях в тонкой стенке, в насадках, коленах, отводах и других элементах стендовых систем. Кавитация может возникать при гидравлических ударах. Явление кавитации неблагоприятно отражается на работе оборудования и приводит к вибрации, шумам, эррозионному разрушению материалов, увеличению гидравлического сопротивления элементов трубопровода и гидросистемы в целом. На возникновение кавитации в основном влияют следующие факторы: 1. Сопротивление жидкости растягивающим напряжениям (здесь надо пояснить это на диаграмме Р-Т). 2. Содержание в жидкости ядер кавитации, т.е. субмикроскопических скоплений газа, или других зародышей новой фазы. 3. Определенные физические и термодинамические свойства жидкости: поверхностное натяжение, давление насыщенных паров, вязкость, способность жидкости к газонасыщению и др. 4. Время прохождения жидкости через зону пониженного давления (время пребывания жидкости в области пониженного давления).
|

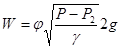 , (27)
, (27) , (28)
, (28)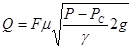 . (29)
. (29)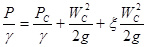 или
или 
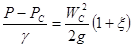 , (30)
, (30) , (31)
, (31) . Обозначив характеристику расширения струи через θ = F2/FС, найдем WС = W2θ и получим
. Обозначив характеристику расширения струи через θ = F2/FС, найдем WС = W2θ и получим (32)
(32)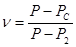 , (34)
, (34) , (35)
, (35) .
.


