Уравнение Бернулли для потока вязкой жидкости.
При движении вязкой жидкости вдоль твердой стенки, например, в трубе происходит торможение потока вследствие влияния вязкости и в результате сил молекулярного сцепления между жидкостью и стенкой. Реализуется неравномерное распределение скоростей: у стенки скорость потока уменьшается до нуля (у смачиваемой жидкости), а в центральной части потока она максимальна (это применительно к течению в трубе). Кроме того движение вязкой жидкости часто сопровождается вращением макрочастиц жидкости, вихреобразованием и перемешиванием. Все это требует затрат энергии, поэтому удельная энергия жидкости (т.е. полный напор) не остается постоянной, как в случае идеальной жидкости, а постепенно расходуется на преодоление сопротивлений и, следовательно, уменьшается вдоль потока. Сказанное можно выразить следующим балансовым уравнением: Нср1 = Нср2 + ∑h, (4) где Нср1 и Нср2 – средние значения полного напора в сечении 1 и 2 соответственно, ∑h – суммарная потеря напора (удельной энергии жидкости) на участке между рассматриваемыми сечениями. Используя это уравнение, запись уравнения Бернулли для случая течения вязкой жидкости представляется в следующем виде
где Σh – суммарная потеря удельной энергии жидкости (напора) на участке между рассматриваемыми сечениями. Энергия, теряемая жидкостью на рассматриваемом участке течения, не исчезает бесследно, а превращается в другую форму – тепловую. Эта энергия непрерывно рассеивается, поэтому повышение температуры жидкости практически мало заметно. Гидравлические потери (общие сведения). Потери напора или, как их часто называют, гидравлические потери зависят от формы, размеров и шероховатости канала (трубы), от скорости течения и вязкости жидкости, но практически не зависят от абсолютного значения давления в жидкости. Как показывает опыт, во многих случаях гидравлические потери приблизительно пропорциональны квадрату скорости потока. Поэтому в гидравлике с давних времен принят следующий общий способ выражения гидравлических потерь полного напора в линейных единицах:
Такое выражение удобно тем, или в единицах давления
Такое выражение удобно тем, что включает в себя безразмерный коэффициент пропорциональности ξ, называемый коэффициентом сопротивления,и скоростной напор, входящий в уравнение Бернулли. Гидравлические потери обычно подразделяют на два вида: местные потери и потери на трение. Местные потери обусловлены так называемыми местными гидравлическими сопротивлениями, т.е. местными изменениями формы и размеров канала (трубы), вызывающими деформацию потока. При этом происходят изменения скорости потока, возникают вихреобразования. Примерами местных сопротивлений могут служить устройства типа задержек потока, сопел, диафрагм, отверстий (шайб), поворотов, вентилей, кранов, другой стендовой арматуры. Местные потери энергии (напора) определяются по формулам:
Последнее уравнение часто называют формулой Вейсбаха. В этих формулах W – средняя по сечению скорость в трубопроводе, в котором установлено местное сопротивление. Каждое местное сопротивление характеризуется своим значением коэффициента сопротивления ξМ, которое во многих случаях приближенно можно считать постоянным для данного вида местного сопротивления. Потери на трение, или потери по длине, - это потери энергии, которые в чистом виде возникают в прямых трубах постоянного сечения, т.е. при установившемся течении, и возрастают пропорционально длине трубы. Этот вид потерь обусловлен трением о поверхность и внутренним трением в жидкости, а поэтому они (потери) имеют место в трубах со сколь угодно малой шероховатостью стенок. Потерю давления на трение можно выразить по общей формуле для гидравлических потерь, т.е. Тогда или
Формулу (9) обычно называют формулой Дарси. Безразмерный коэффициент λ называется коэффициентом потерь на трение или коэффициентом сопротивления трения. Гидравлические потери в напорных потоках происходят за счет уменьшения вдоль потока удельной потенциальной энергии жидкости (Z + Р/γ). Удельная кинетическая энергия жидкости в этом случае если и меняется вдоль потока при заданном расходе, то не за счет потерь энергии, а вследствие изменения поперечного сечения канала, так как она зависит только от скорости, а скорость определяется объемным расходом Q и площадью сечения S: W = Q/S. Следовательно, в трубе постоянного сечения средняя скорость и удельная кинетическая энергия остаются строго постоянными, несмотря на наличие гидравлических потерь напора. Расчет гидравлических потерь для разных конкретных случаев представляет собой один из основных вопросов гидравлики.
2. РЕЖИМЫ ТЕЧЕНИЯ ЖИДКОСТЕЙ В ТРУБАХ Возможны два режима или два вида течения жидкостей в трубах: ламинарное, т.е. слоистое, течение и турбулентное, т.е. бурное, возмущенное. Ламинарное течение – это течение без перемешивания слоев и частиц (макрочастиц) жидкости, без пульсаций скорости. Это течение является вполне упорядоченным и при постоянном напоре строго установившимся. Однако ламинарнре течение нельзя считать безвихревым. Хотя в нем нет ярко выраженных вихрей, но одновременно с поступательным движением жидкости имеет место упорядоченное вращательное движение отдельных частиц жидкости вокруг своих мгновенных центров вращения. Турбулентное течение – это течение, сопровождающееся интенсивным перемешиванием жидкости и пульсациями скоростей и давлений. Движение отдельных частиц оказывается неупорядоченным, траектории фрагментов жидкости имеют подчас вид замысловатых кривых. Это объясняется тем, что при турбулентном течении наряду с продольным перемещением массы жидкости имеют место поперечное и вращательное движения отдельных, как бы автономных, объемов жидкости. Смена режима течения данной жидкости в трубе происходит при определенной скорости течения, которую называют критической (Wкр). Как показывают эксперименты, значение этой скорости прямо пропорционально кинематическому коэффициенту вязкости (ν) и обратно пропорционально диаметру трубы (d), т.е. Wкр = kν/d. Оказывается, что входящий в предыдущее соотношение безразмерный коэффициет k имеет универсальное значение, т.е. он одинаков для всех жидкостей и труб любых диаметров. Это означает, что смена режимов течения происходит при вполне определенном соотношении, которое можно выразить числом, между скоростью, диаметром трубы и вязкостью жидкости. Это безразмерное число называется критическим числом Рейнольдса по имени английского ученого, который экспериментально установил этот критерий:
Как показывает опыт, критическое число Рейнольдса приблизительно равно 2300. Однако можно говорить не только о критическом числе Рейнольдса, определяющим смену режима течения, но и о числе Рейнольдса, характеным для того или иного потока, и выражать его через фактическую скорость потока, т.е.
Таким образом, мы получили критерий, позволяющий судить о режиме течения жидкости в трубе. При значениях числа Rе < RеКР течение называется ламинарным; при Rе > RеКР течение обычно турбулентное. Смена режимов течения при достижении числа RеКР объясняется тем, что один режим течения теряет устойчивость, а другой ее приобретает. При Rе < RеКР ламинарный режим является вполне устойчивым; всякого рода искусственная турболизация потока и его возмущения (сотрясение трубы, введение в поток колебаний и действия прочих возмущающих факторов) погашаются влиянием вязкости и ламинарный поток восстанавливается. Возникающий при этом турбулентный поток неустойчив. При Rе > RеКР, наоборот, турбулентный поток устойчив, а ламинарный – неустойчив. В связи с этим критическое число Рейнольдса, соответствующее переходу от ламинарного режима к турбулентному, может получиться несколько больше, чем для обратного перехода. Гидродинамическое подобие. Гидродинамическое подобие – это подобие потоков несжимаемой жидкости, включающее в себя подобие геометрическое, кинематическое и динамическое. Геометрическое подобие, как известно из геометрии, означает пропорциональность сходственных размеров и равенство соответствующих углов. В гидравлике под геометрическим подобием понимается подобие поверхностей, которые ограничивают потоки жидкостей, т.е. подобие трубных каналов. Кинематическое подобие – это геометрическое подобие канала и пропорциональность скоростей в сходственных сечениях. Динамическое подобие означает пропорциональность сил, действующих на сходственные элементы кинематически подобных потоков Осуществление на практике полного гидродинамического подобия оказывается весьма затруднительным, поэтому имеют, обычно, дело с частичным (неполным) подобием, при котором наблюдается пропорциональность лишь главных, основных для процесса, сил. Физический смысл числа Рейнольдса заключается в том, что это – величина, пропорциональная отношению динамического давления к напряжению трения или, что то же самое, отношение сил инерции к силам вязкости. Поэтому закон гидродинамического подобия формулируется следующим образом: для гидродинамического подобия геометрически подобных потоков с учетом сил вязкости требуется равенство чисел Рейнольдса, подсчитанных для любой пары сходственных сечений этих потоков.
МЕСТНЫЕ ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ Мы уже говорили, что гидравлические потери энергии делятся на две категории: местные потери и потери на трение. Рассмотрим более подробно потери, обусловленные местными гидравлическими сопротивлениями, т.е. такими элементами трубопровода, в которых вследствие изменения размеров или конфигурации канала происходит изменение скорости потока и возникают вихреобразования. Общий способ их выражения основан на экспериментальных данных и имеет следующий вид:
где Q – объемный расход, м3/с. Задача теперь заключается в том, чтобы научиться определять коэффициенты сопротивления для различных трубных элементов, т.е. местных сопротивлений. Простейшие местные гидравлические сопротивления можно разбить на следующие группы и подгруппы: 1. Расширение трубопровода (канала) – внезапное, плавное. 2. Сужение трубопровода (канала) – внезапное, плавное. 3. Поворот трубопровода (канала) – внезапный, плавный. Более сложные случаи местных сопротивлений представляют собой комбинации перечисленных простейших сопротивлений. Рассмотрим некоторые местные сопротивления при турбулентном режиме течения. Следует отметить, что коэффициенты сопротивления ξМ при турбулентном течении определяются почти исключительно формой гидравлического элемента и очень мало меняются с изменением размеров канала, скорости потока и вязкости жидкости. Поэтому их считают независящими от числа Рейнольдса, что означает автомодельность по числу Rе. Значения коэффициентов местных сопротивлений в большинстве случаев получают экспериментальным путем, а затем пользуются обобщенными формулами или графиками. Однако для некоторых типов местных сопротивлений, а именно для внезапного расширения или для течения в диффузоре расчетные значения коэффициентов сопротивления имеют удовлетворительную точность. ДАЛЕЕ СЛЕДУЕТ ДЕМОНСТРАЦИЯ РИСУНКОВ МЕСТНЫХ ГИДРАВЛИЧЕСКИХ СОПРОТИВЛЕНИЙ, ВКЛЮЧАЯ СХЕМУ ВЕНТИЛЯ (рис.2) Местные гидравлические сопротивления при ламинарном режиме. Расчет потери напора на местных сопротивлениях при ламинарном режиме имеет особенности. Во - первых, местные сопротивления ври этом режиме играют меньшую роль по сравнению с потерями трения. Во – вторых, закон сопротивления в этом случае является более сложным и исследован в меньшей степени, чем при турбулентном режиме. Если при турбулентном режиме потери напора на мастном сопротивлении не зависят от числа Рейнольдса, то при ламинарном режиме потерю напора hм следует рассматривать как сумму: hм = hтр + hвихр, (13) где hтр – потеря напора, обусловленная непосредственным действием сил трения (вязкости) в данном местном сопротивлении, пропорциональная вязкости жидкости и скорости в первой степени; hвихр – потеря, связанная с отрывом потока и вихреобразованиями, возникающими в самом местном сопротивлении или за ним, и пропорциональная квадрату скорости. Так, например, при течении через жиклер (рис. 3) слева от сечения 1. – 1 возникает потеря напора на трение, а справа – на вихреобразования. Формулу (12) можно представить в следующем виде:
где А и В – безразмерные константы, зависящие от формы местного сопротивления. Разделив, согласно общему принципу определения коэффициента сопротивления, hм на скоростной напор, получим общее выражение для коэффициента местного сопротивления при ламинарном режиме
Соотношение между первым и вторым членами в формулах (14 и 15) зависит от формы местного сопротивления и числа Rе. При широком диапазоне изменения числа Рейнольдса в одном и том же местном сопротивлении возможны как линейный (при малых числах Rе) так и квадратичный (при больших числах Rе) законы сопротивления, а также переходная между ними область сопротивления при средних числах Rе. Типичный график, иллюстрирующий сказанное, приведен на рис.. Такого рода графики для конкретных сопротивлений обычно строят на основе экспериментальных данных. Иногда вместо двухчленной формулы выражения местных гидравлических потерь применяют степенной одночлен вида
где k – размерная величина; m – показатель степени, зависящий от формы местного сопротивления и числа Рейнольдса и изменяющийся в пределах от 1 до 2.
ТЕЧЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ОСНОВНЫЕ РАСЧЕТНЫЕ ЗАВИСИМОСТИ
Ламинарное течение жидкости в круглой трубе. Как уже говорилось,ламинарное течение является строго упорядоченным слоистым течением без перемешивания жидкости; оно подчиняется закону трения Ньютона, суть которого в следующем: касательное напряжение в жидкости зависит от рода жидкости и характера течения и при слоистом течении изменяется прямо пропорционально поперечному градиенту скорости, т.е.
где μ – динамический коэффициент вязкости; наряду с динамическим коэффициентом вязкости μ применяется в гидравлике кинематический коэффициент вязкости ν, равный ν = μ/ρ, где ρ – плотность жидкости. (Размерность μ, н·сек / м2; размерность ν, м2/сек). Используя этот закон, находится распределение скоростей по сечению круглой трубы в ламинарном режиме течения жидкости и формула для определения расхода:
где Ртр – перепад давления на участке трубы длиной ℓ, т.е. это потери от трения (потери трения). Зная, что потери напора за счет трения определяются как hтр = Ртр/γ, находим
Заменяя μ через νρ и γ через ρg, а также переходя от r0 к d = 2r0, окончательно находится выражение
Полученный закон сопротивления показывает, что при ламинарном течении жидкости в круглой трубе потеря напора на трение пропорциональна расходу (скорости) и вязкости в первой степени и обратно пропорциональна диаметру в четвертой степени. Этот закон, часто называемый законом Пуазейля – Хагена, используется для расчета трубопроводов с ламинарным режимом течения. Так как по общему принципу (закон Дарси) Связь средней скорости с потерей напора Сопоставляя полученное выражение с формулой Дарси, видим, что Эту зависимость называют законом Пуазейля. Зная закон распределения скоростей по сечению трубы и связь средней скорости с потерей напора, возможно определить значение коэффициента α, учитывающего неравномерность распределения скоростей в уравнении Бернулли (5). Для ламинарного течения α1 = α2 =2 Теория ламинарного течения жидкости в круглой трубе, элементы которой были изложены в данном курсе, в общем хорошо подтверждается опытом. Полученные законы сопротивления и распределения скоростей не нуждаются в каких-либо поправках, за исключением следующих случаев. 1. При течении в начальном участке трубы, где происходит постепенное установление параболического профиля скоростей. Сопротивление на этом участке получается больше, чем на последующих участках трубы. Но это обстоятельство учитывается только при расчете очень коротких труб. 2. При течении со значительным теплообменом. 3. При очень высоких перепадах давления. Потеря напора на участке трубы, длина которого ℓ меньше длины начального участка ℓн ач, определяется по формулам (20 и 21), но с поправочным коэффициентом К, большим единицы. Так при ℓ = ℓнач К = 1,09. Для коротких труб значение поправочного коэффициента К существенно отличается от единицы. Определить длину начального участка можно по приближенной формуле Шиллера: ℓ/d = 0,029Rе. (22) В литературных источниках встречаются и другие оценочные зависимости для определения длины начального участка ℓнач = 0,061Rеd В том случае, когда длина трубы ℓ больше длины начального участка ℓнач, потеря напора будет складываться из потери на начальном участке и потери на участке стабилизированного течения:
Если относительная длина трубопровода ℓ/d достаточно велика, то дополнительный член в скобках, равный 0,165 можно не учитывать. Течение с теплообменом. При течении жидкости, которое сопровождается ее охлаждением, слои жидкости, непосредственно прилегающие к стенке, имеют температуру более низкую, а вязкость более высокую, чем в основном ядре потока. Это ведет к более сильному торможению пристенных слоев жидкости и уменьшению градиента скорости у стенки. При течении, сопровождающемся нагреванием жидкости через стенку, ситуация меняется наоборот: вязкость пристенных слоев уменьшается, пристенный градиент скорости возрастает. Таким образом, в результате теплообмена через стенку трубы происходит нарушение обычного параболического закона распределения скоростей. Это показано на рис.. Здесь 1 – распределение скоростей при изотермическом течении, 2 – при течении с охлаждением, 3 – при течении с нагреванием. Это вызывает изменение коэффициента α в уравнении Бернулли: охлаждение ведет к усилению неравномерности распределения скоростей (α > 2), нагревание ослабляет эту неравномерность (α < 2). Напомним, что при параболическом распределении α = 2. Изменение профиля скоростей вызывает изменение закона сопротивления. Приближенно это можно учесть следующей формулой:
где Rе – число Рейнольдса, подсчитанное по средней вязкости жидкости; νЖ – средняя вязкость жидкости; νст – вязкость жидкости, соответствующая средней температуре стенки. Для более точных расчетов существуют специальные зависимости Особые случаи ламинарного течения. К таким видам течения относится течение жидкости в зазорах. Зазоры могут быть образованы неподвижными стенками, одна из стенок, образующих зазор, может быть подвижной. Зазоры могут быть симметричными и асимметричными, плоскими и кольцевыми. Течение при больших перепадах давления. Этот вид течения реализуется в капиллярах и малых зазорах. В этом случае падение напора вдоль потока оказывается существенно нелинейным, а закон Пуазейля дает заметную погрешность. Облитерация. Иногда при течении жидкости через капилляры и малые зазоры наблюдается явление, которое не может быть объяснено законами гидравлики. Оно заключается в том, что расход жидкости через капилляр или зазор с течением времени уменьшается несмотря на то, что перепад давления, под которым происходит движение жидкости, и ее физические свойства остаются неизменными. Причина этого явления кроется в том, что при определенных условиях происходит как бы засорение или заращивание канала твердыми частицами. Этот процесс носит название облитерации и заключается в том, что на поверхности раздела твердого тела и жидкости под действием молекулярных и электромагнитных сил, возникающих между стенкой и жидкостью, происходит явление, похожее на адсорбцию, т.е. уплотнение жидкости до практически твердого состояния на поверхности стенки. Степень облитерации зависит от молекулярной структуры жидкости, причем в большей степени проявляется в сложных, высокомолекулярных жидкостях (жидкости на керосиновой основе). С повышением температуры интенсивность облитерации понижается. Повышение перепада давления, под которым происходит движение жидкости через капилляр или зазор, наоборот увеличивает степень облитерации. В целях избежания облитерации в жиклерах и дросселях не рекомендуется отверстия делать меньше 0,2…0,4 мм. Турбулентное течение. Турбулентное течение жидкости в гладких трубах Как уже сообщалось, для турбулентного течения характерно перемешивание жидкости, пульсации скоростей и давлений в процессе течения. Ввиду того, что при турбулентном течении отсутствует слоистость потока, закон трения Ньютона в этом случае неприменим. Вследствие перемешивания жидкости и непрерывного переноса количества движенияв поперечном направлении касательное напряжение на стенке трубы в турбулентном потоке значительно больше, чем в ламинарном при тех же значениях динамического давления, подсчитанного по средней скорости потока. Распределение скоростей при турбулентном режиме течения более равномерно. В связи с этим коэффициент α, учитывающий неравномерность распределения скоростей в уравнении Бернулли, оказывается меньше, чем при ламинарном течении, в диапазоне 1…1,13: при Rе = Rекр, α = 1,13; при, Rе = 3·106, α = 1,025,т.е. α асимптотически приближается к единице. В большинстве случаев для практических расчетов, связанных с турбулентным течением жидкостей в трубах, пользуются экспериментальными данными, систематизированными на основе гидродинамической теории подобия. Основной расчетной формулой для турбулентного течения в круглых трубах является уже рассмотренная нами универсальная формула:
или если скорость потока выразить через расход. Видим, что при турбулентном течении потеря напора на трение пропорциональна квадрату скорости потока (и квадрату расхода). Но из закона гидродинамического подобия следует, что коэффициент λТ как и коэффициент λЛ должен являться функцией числа Рейнольдса, содержащего скорость потока, вязкость жидкости и диаметр трубы
Существует ряд эмпирических и полуэмпирических формул, представляющих эту зависимость для турбулентного течения в гладких трубах. Одной из наиболее удобных и употребительных зависимостей является формула Конакова, которая имеет следующий вид:
Эта формула применима от Rе = Rекр до Rе, равного нескольким миллионам. При числах Рейнольдса от 2300 до ≈ 105 можно пользоваться формулой Блазиуса
Из формул (24) и (25) видно, что коэффициент λ уменьшается с увеличением числа Рейнольдса, но это уменьшение гораздо менее значительно, чем при ламинарном режиме. Приведенные формулы для определения коэффициента потерь на трение через число Rе справедливы для так называемых технически гладких (гидравлически гладких) труб, т.е. для таких, шероховатость которых столь мала, что практически не влияет на сопротивление. Именно такие трубы применяются в стендовой практике. Экспериментально установлено, что при турбулентном режиме существуют три области, в которых коэффициент λ по-разному зависит от числа Rе: 1. Область гидравлически гладких труб. 2. Переходная область. 3. Область гидравлически шероховатых труб. Физическая картина существования этих областей в одной и той же трубе объясняется следующим образом. У всякой трубы на стенке имеются выступы шероховатости. Их высота зависит от материала труб технологии их изготовления, времени эксплуатации и др. факторов. В турбулентном потоке скорости непосредственно у стенки равны нулю. Поэтому вблизи стенок образуется тонкий слой жидкости толщиной δ, где скорости столь малы, что в его пределах движение жидкости близко к ламинарному. Этот слой, толщина которого измеряется долями миллиметра, называется вязким (ламинарным) подслоем (рис. 4). Если через Δ обозначить среднюю высоту выступов шероховатости, то возможны следующие соотношения δ и Δ. При δ > Δ выступы шероховатости прикрыты вязким подслоем, турбулентная часть потока не касается выступов и скользит по ламинарному слою, как по гладкой трубе. В этом случае трубы рассматриваются как гидравлически гладкие и потери давление на трение не зависят от шероховатости трубы. Если δ < Δ, то выступы шероховатости вклиниваются в турбулентную зону и в них ударяются жидкие макрочастицы турбулентного ядра потока. В этом случае потери напора, коэффициент λ, зависят от шероховатости трубы. Толщина ламинарного подслоя зависит от числа Рейнольдса (при увеличении числа Rе толщина ламинарного подслоя уменьшается). Поэтому понятия гидравлически гладкой стенки и шероховатой относительны. Поскольку выступы шероховатости неодинаковы, то пользуются понятием относительной шероховатости Δэкв, т.е. считают шероховатость равнозернистой, но потери давления на трение при этом равны потерям напора при действительной шероховаиости. Значения Δэкв приведены в справочниках. Эквивалентная шероховатость в зависимости от диаметра трубы по-разному сказывается на величине гидравлических сопротивлений. Для учета этого фактора в гидравлике используют понятия относительной шероховатости Δэкв/d или относительной гладкости d/Δэкв. Коэффициент гидравличесого трения λ при турбулентном режиме в зависимости от числа Rе и относительной гладкости (рис 5) распределен по областям и характерен зля каждой области (зоны). Для каждой зоны существуют рекомендованные формулы для вычисления коэффициента сопротивления λ. Они приводятся в справочниках и ли в учебной литературе. Турбулентное течение в некруглых трубах. Иногда приходиться иметь дело с турбулентным течением в некруглых трубах. Так каналы охлаждения камеры ЖРД представляют собой трубы некруглого сечения. Рассмотрим расчет потерь на трение при турбулентном течении в трубе с поперечным сечением произвольной формы. Суммарную силу трения, действующую на внешнюю поверхность потока длиной ℓ, можно выразить следующим образом: Т = Пℓτ0, где П – периметр сечения (его называют еще смоченным периметром); τ0 – касательное напряжение на стенке, зависящее от динамического напора, т.е. от средней скорости течения (от расхода) и плотности жидкости. Итак, при заданной площади сечения и при данном расходе жидкости сила трения пропорциональна периметру сечения. Для количественной оценки влияния формы сечения на потерю напора вводится в расчет так называемый гидравлический радиус Rг, равный отношению площади сечения трубы к его периметру: Rг = S/П. Для круглого сечения имеем Rг = d/4, тогда имеем d = 4Rг, поэтому часто применяется для расчетов потерь напора в трубах некруглого сечения понятие гидравлического диаметра, равного dг = 4Rг. Воспользуемся основной формулой для расчета потери напора на трение, формула
Гидравлический удар в трубопроводе. Гидравлический удар представляет собой колебательный процесс, возникающий в упругом трубопроводе с малосжимаемой жидкостью при внезапном изменении ее скорости или давления. Гидравлический удар чаще всего возникает вследствие быстрого закрытия или открытия крана (клапана) или другого устройства управления потоком. Особенно опасен гидравлический удар в длинных трубопроводах большого диаметра, в которых огромные массы жидкости движутся с большими скоростями. Теорию гидравлического удара разработалН. Е. Жуковский в 1898 г. Он установил, что гидравлический удар в трубе является нестационарным быстропротекающим периодическим процессом, который сопровождается упругими деформациями жидкости и стенок трубы. Величина давления, сформировавшегося за счет ударной волны, определяется по следующей формуле Для ослабления гидравлического удара следует увеличивать время перекрытия трубопровода. Кроме того, разработаны и применяются различные способы борьбы с гидроударом: установка предохранительных клапанов, установка компенсаторов, установка в определенных точках трубопровода обратных клапанов. Иногда предпочтительным решением является не уменьшение ударного давления, а увеличение прочности слабых звеньев трубопроводной системы.
|

 , (5)
, (5) (6)
(6) .
. или
или 
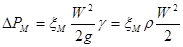 (7)
(7) , однако более удобнее будет коэффициент ξТР связать с относительной длиной трубы ℓ/d соотношением ξТР = λℓ/d.
, однако более удобнее будет коэффициент ξТР связать с относительной длиной трубы ℓ/d соотношением ξТР = λℓ/d.
 (8)
(8) (9)
(9) (10)
(10) (11)
(11) , (12)
, (12) , (14)
, (14)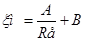 (15)
(15) ,
, , (17)
, (17) (18)
(18) (19)
(19) тр
тр  , тогда, заменяя Q = Wср π
, тогда, заменяя Q = Wср π  , окончательно получим
, окончательно получим  . (20)
. (20)
 (21)
(21) или с учетом (21) и (22)
или с учетом (21) и (22)
 , (23)
, (23)
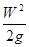 ,здесь λ ≡ λТ – коэффициент потерь на трение при турбулентном режиме
,здесь λ ≡ λТ – коэффициент потерь на трение при турбулентном режиме ,
,
 (24)
(24) (25)
(25) , выразив диаметр трубы через гидравлический диаметр, получим
, выразив диаметр трубы через гидравлический диаметр, получим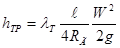 . Эта формула является более общим выражением закона потерь напора, она справедлива для круглых и некруглых труб. При этом коэффициент λ подсчитывается по формулам для круглых труб, а число Рейнольдса выражается через гидравлический диаметр, где dг = 4Rг:
. Эта формула является более общим выражением закона потерь напора, она справедлива для круглых и некруглых труб. При этом коэффициент λ подсчитывается по формулам для круглых труб, а число Рейнольдса выражается через гидравлический диаметр, где dг = 4Rг: (26)
(26) , где W0 – средняя скорость потока, ТЗ – время перекрытия трубы управляющим органом.
, где W0 – средняя скорость потока, ТЗ – время перекрытия трубы управляющим органом.


