Течения в местных сопротивлениях
Для характеристики кавитационных свойств местных гидравлических сопротивлений обычно пользуются различными безразмерными параметрами (их часто называют критериями) кавитации. Одним из наиболее важных параметров является число кавитации
здесь Р и W – характерные величины давления и скорости, Ркав минимальное давление в потоке, при котором возникает кавитация, ρ – плотность жидкости. Рассмотрим, в качестве примера, течение жидкости в простейшем типе местного сопротивления: в трубе Вентури (рис. 3).
     
Видим, что при использовании формулы (11) давление Ркав заменяется на давление насыщенных паров жидкости Рн, полагая, что давление внутри кавитационной каверны равно Рн. Эта замена не справедлива, но оправдана, т.к. точно определить истинное давление в зоне кавитации трудно. Часто ошибка измерения сопоставима с ΔР = Ркав – Рн. В некоторых случаях, например, при определении кавитационных характеристик (кавитационных режимов) регулирующей аппаратуры используются упрощенные критерии кавитации в виде коэффициента, определяющего бескавитационный перепад давления:
β = (Р1 – Р2)кав/Р1 или k1 = (Р1/Р2)кав или σ = (Р2 – Рн)/(Р1 – Р2) (12)
Видим, что для характеристики кавитационного течения в местных гидравлических сопротивлениях используется большое разнообразие формул, дающих различные численные значения для одних и тех же условий течения жидкости, но между этими критериями можно установить связи, т.е. они не являются независимыми характеристиками. Например, КС = 1/(σ + 1) Но преимущественно используется запись для числа кавитации в форме выраженияй(8) или (9). Первые признаки кавитации наблюдаются, когда число кавитации χ становится меньше некоторого критического числа χкр, величина которого зависит от конструктивных особенностей запорного или регулирующего органа (стендового агрегата), а также от теплофизических свойств жидкости. При известной величине χкр нетрудно вычислить скорость потока, при которой возникает кавитация:
Для простых видов сопротивлений: плавные сужения, расширения, повороты и др. – эта связь может быть установлена расчетным путем. Для сложных (комбинированных) местных сопротивлений, каковыми являются стендовые агрегаты, связь ξ с χкр устанавливается экспериментально. На рис. 4 представлены результаты установления этой связи опытным путем для потоков воды. Влияние кавитации на гидравлическое сопротивление на данном рисунке выявлено очень убедительно. Бескавитационное течение характеризуется практически постоянным значением ξ, кторое сохраняется до критического значения числа кавитации χкр При χ < χкр коэффициент сопротивления ξ резко возрастает, этому моменту соответствует минимальное критическое число кавитации χ кр мин Эта ситуация соответствуе максимально достижимому расходу через местное сопротивление (через клапан). В этих экспериментальных исследованиях использовался коэффициент ξу (обобщенный коэффициент гидравлического сопротивления стендового агрегата в целом), который определялся по формуле
где ΔР – перепад давления на агрегате (на клапане) как на общем сопротивлении; FУ – площадь условного прохода клапана; ρ – плотность жидкости; Q – объемный расход.
На рис. 5 представлена зависимость χкр от ξ для течения аммиака в бескавитационном режиме (т.е. аналогично рис. 4). Сравнение полученных экспериментальных данных (т.е. аммиака и воды) показывает вполне удовлетворительное совпадение. Этот результат позволяет распространить полученные на воде экспериментальные зависимости χкр от ξу на другие ньютоновские жидкости, т.е. когда касательное напряжение прямо пропорционально поперечному градиенту скорости: τ = μ Пдтверждение этому дают рис 6 и 7, на которых представлены зависимости чисел кавитации от коэффициента сопротивления для различных типоразмеров регулирующих клапанов в бескавитационном режиме. Сравнение экспериментальных данных, полученных на воде и аммиаке вполне удовлетворительное. Это позволяет распространить полученные экспериментальные данные на воде на другие жидкости. Полученные экспериментальные данные могут быть обобщены и использованы в практических расчетах Анализ теоретических зависимостей и экспериментальных данных по критическим параметрам кавитации показывает, что предотвращение явления кавитации в местных гидравлических сопротивлениях достигается следующими способами: 1. Изменением гидравлических режимов работы местного сопротивления. 2. Выбором соответствующего типа и геометрических характеристик местного сопротивления, обеспечивающих бескавитационную работу в заданных пределах изменения расхода и давления потока жидкости. 3. Многоступенчатым дросселированием потока жидкости, при котором общий перепад давления распределяется между отдельными дроссельными элементами. Для реализации указанных способов предотвращения кавитации во всех случаях необходимо иметь аналитические зависимости или опытные данные по критериям начала кавитации. Если по условиям эксплуатации такими способами невозможно исключить кавитацию в принятом типе местного сопротивления, то необходимо выбрать другой тип местного сопротивления, имеющий более высокое значение коэффициента каитации (более высокий запас по кавитации).
|

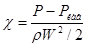 , (7)
, (7)
 (8)
(8) (9)
(9) ; (10)
; (10) 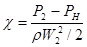 (11)
(11) (13)
(13) Дальнейшая задача формулируется следующим образом: необходимо отыскать связь между χкр и коэффициентом гидравлического сопротивления для бескавитационного режима течения, т.е. с ξ. кси
Дальнейшая задача формулируется следующим образом: необходимо отыскать связь между χкр и коэффициентом гидравлического сопротивления для бескавитационного режима течения, т.е. с ξ. кси , (124
, (124 (15)
(15) .
.


