Выбор расчетной схемы. -на пластинку наносится квадратная сетка с шагом λ=1м;
-на пластинку наносится квадратная сетка с шагом λ=1м;
- учитывая симметрию нумеруются узлы сетки (рис.2)
- неизвестны прогибы в узлах 1,2,3,4 в точках на контуре (линии AB,CD,BC,AD) и на оси косой симметрии (линия EF) прогибы известны – равны нулю
2. Составление системы уравнений.
Составляем уравнениe Софи Жермен
d4W/dx4+2d4W/dx2dy2+d4W/dy4=qz/D
в конечно разностном виде для внутренних узлов (1,2,3,4) используя шаблон (рис.3)
В=q*λ4/D - правая часть уравнения
Сосредоточенную силу в узле 3 заменяем распределенной нагрузкой в пределах шага сетки интенсивностью qz=P/λ2, следовательно, правая часть уравнения для узла 3. ………….примет вид Рλ2/D
20W1-8(W2+W3)+2W4+W1=qz*λ4/D
20W2-8(W1+W4)+2W3+W2=qz*λ4/D
20W3-8(2W1+W4)+4W2-W3=P*λ2/D
20W4-8(2W2+W3)+4W1-W4=0
Проверяем симметрию матрицы коэффициентов: если уравнен. 3 и 4 домножить на 0,5 – матрица будет приведена к симметричному виду.
3. Решаем систему уравнений с помощью ЭВМ по стандартной программе
Результаты решения: прогибы в точках пластины W1=3.607/D, W2=3.435/D, W3=4.545/D, W4=4.047/D.
Проверка правильности полученного решения
Система уравнений решена правильно.
4. Вычисляем усилия в точках пластины.
Изгибающите моменты Мх, Му, крутящий момент Мху и поперечные силы Qx, Qy определяем используя конечно разностные шаблоны
Mx=-D(d2W/dx2+μd2W/dy2); My=-D(d2W/dx2+ μd2W/dy2);
|
| -1,17
| -1,23
|
| 1,23
| 1,17
|
| |
| 3,74
| 4,23
|
| -4,23
| -3,74
|
| |
| 3,75
| 5,36
|
| -5,36
| -3,75
|
| |
| 3,74
| 4,23
|
| -4,23
| -3,74
|
| |
| -1,17
| -1,23
|
| 1,23
| 1,17
|
|
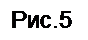
| Значения изгибающих моментов Му в точках пластины (кНм/м) Табл.2
| |
|
| -6,87
| -7,21
|
| 7,21
| 6,87
|
| |
| 3,38
| 3,31
|
| -3,31
| -3,38
|
| |
| 1,83
| 2,73
|
| -2,73
| -1,83
|
| |
| 3,38
| 3,31
|
| -3,31
| -3,38
|
| |
| -6,87
| -7,21
|
| 7,21
| 6,87
|
|
w
| | | | | определим значения крутящих моментов по шаблону
| |
Mxy=-D(1- μ)d2W/dxdy
| | | | | | | | 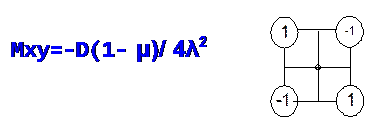 | | | | | | Например, для точки 1: Mxy(1)=-D(1- μ)/4λ2*W4)=-0,83*4,047/4=-0,84 кНм/м.
| |
|
|
|
|
|
|
|
| | 1,68
| 0,94
| -0,84
| -1,89
| -0,84
| 0,94
| 1,68
| |
|
|
|
|
|
|
| | -1,68
| -0,94
| 0,84
| 1,89
| 0,84
| -0,94
| -1,68
| |
|
|
|
|
|
|
|
|
| -3,607
| 3,435
| 7,214
| 3,435
| -3,607
|
| | Rx(b)=-8,42
| 3,22
| -3,04
| -6,45
| -3,04
| 3,22
|
| | Rx(a)=-5,78
| 3,46
| -2,39
| -6,92
| -2,38
| 3,46
|
| | Rx(b)=-8,42
| 3,22
| -3,04
| -6,45
| -3,04
| 3,22
|
| |
| -3,607
| 3,435
| 7,214
| 3,435
| -3,607
|
| 
| | | | | | | | | |  | | | | | | | Qy =-D d/dx*(d2W/dx+d2W/dx2)+d2W/dy2.
| | | | | | | Значения поперечных сил Qy (кН/м). Табл.5
| |
w
|
| Ry(d)=--16,2
| Ry(e)=1-7,4
| Ry(f)
| Ry(e)
| Ry(d)
|
| |
| -5,82
| -7,07
|
| 7,07
| 5,82
|
| |
|
|
|
|
|
|
| |
| 5,82
| 7,07
|
| -7,07
| -5,82
|
| |
| Ry(d)=-1-6,2
| Ry(e)=--17,4
| Ry(f)
| Ry(e)
| Ry(d)
|
|
w
w
μ
| | | | | | | | | | | | | | | | | | Реакции опор в точках d,e (Ry) определим используя разрешающее уравнение для точек на контуре, где В=1/D*(2 λ3Ry(ij)
| | | | | | |  | | | | | | | Например, для точки d
1/D*(2 λ3λ3*Ry(d))=-2(1+ μ)W2-2(7- μ)W2+ μW1+(4- μ)W1+2W4; отсюда
Ry(d)=1/2λ3*(3,34*3,435-13,66*3,435+
0,17*3,607+3,83*3,607+2*4,047=-16,22кН/м
| | | | | | | | Реакции опор в точках a,b (Rx) определим используя разрешающее уравнение для точек на контуре, где В=1/D*(2 λ3Rx(ij)
| |
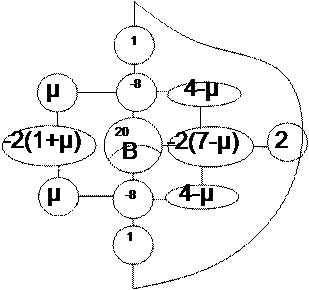
| | | | | Например, для точки d
1/D*(2λ3*Rx(d))=2(1+ μ)W2-2(7- μ)W2- μW4+(4- μ)W4+2W1; отсюда
Rx(d)=1/2λ3*(3,34*3,435-13,66*3,435-
0,17*4,047+3,83*4,047+3,607=-8,43 кН/м
| |


| | | | | Например, (4 λ2Rугловое)/D= 2μW(2)- 2μW(2)+ 4(2-μ)W(2);
Следовательно, Rугловое=D/4 λ2*(1,83*4*3,435)=6,28 кН.
| |
РЕЗУЛЬТАТЫ ПОЛУЧЕННЫЕ ПО ПРОГРАММЕ EXCEL
Прогибы точек пластины (множитель1/D)
|
|  0 0
| 3,435
| 3,607
|
| -3,607
| -3,435
|
| |
|
|
|
|
|
|
|
| | -3,435
|
| 3,435
| 3,607
|
| -3,607
| -3,435
|
| | -4,047
|
| 4,047
| 4,545
|
| -4,545
| -4,047
|
| | -3,435
|
| 3,435
| 3,607
|
| -3,607
| -3,435
|
| |
|
|
|
|
|
|
|
| |
|
| 3,435
| 3,607
|
| -3,607
| -3,435
|
| Изгибающие моменты силы Мх
|
| -1,1679
| -1,22638
|
| 1,22638
| 1,1679
|
| |
| 3,74291
| 4,23273
|
| -4,23273
| -3,74291
|
| |
| 3,75708
| 5,36192
|
| -5,36192
| -3,75708
|
| |
| 3,74291
| 4,23273
|
| -4,23273
| -3,74291
|
| |
| -1,1679
| -1,22638
|
| 1,22638
| 1,1679
|
| |
|
|
|
|
|
|
| |
Изгибающие моменты силы Му
| 
|
|
|
|
|
| |
| 3,37771
| 3,31143
|
| -3,31143
| -3,37771
|
| |
| 1,82733
| 2,73331
|
| -2,73331
| -1,82733
|
| |
| 3,37771
| 3,31143
|
| -3,31143
| -3,37771
|
| |
| -6,87
| -7,214
|
| 7,214
| 6,87
|
|
|
|
|
|
|
|
|
| | 1,679505
| 0,943088
| -0,83975
| -1,88618
| -0,83975
| 0,943088
| 1,679505
| |
|
|
|
|
|
|
| | -1,67951
| -0,94309
| 0,839753
| 1,886175
| 0,839753
| -0,94309
| -1,67951
| |
|
|
|
|
|
|
|
|
|
| Поперечные силы Qx
|
| |
| -3,607
| 3,435
| 7,214
| 3,435
| -3,607
|
| | -8,42909
| 3,224
| -3,043
| -6,448
| -3,043
| 3,224
| -8,429
| | -5,78892
| 3,4595
| -2,3865
| -6,919
| -2,3865
| 3,4595
| -5,7889
| | -8,42909
| 3,224
| -3,043
| -6,448
| -3,043
| 3,224
| -4,2145
| |
| -3,607
| 3,435
| 7,214
| 3,435
| -3,607
|
|
|
|
| Поперечные силы Qy
|
| |
| -16,2
| -17,4
|
| 17,44
| 16,22
|
| |
| -5,8215
| -7,0665
|
| 7,0665
| 5,8215
|
| |
| -4,4E-16
| -2,2E-16
|
| 2,22E-16
| 4,44E-16
|
| |
| 5,8215
| 7,0665
|
| -7,0665
| -5,8215
|
| |
| -16,2
| -17,4
|
| 17,2
| 16,22
|
| |
|
|
|
|
|
|
|
|
| Опорные реакции
|
|
| | 6,28805
| -16,2
| -17,4
|
| 17,44
| 6,28805
| | -8,4291
|
|
|
|
| -8,4291
| | -5,7889
|
|
|
|
| -5,7889
| | -8,4291
| -16,2
| -17,4
|
| 17,44
| -8,4291
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|
Измерение следующих дефектов: ползун, выщербина, неравномерный прокат, равномерный прокат, кольцевая выработка, откол обода колеса, тонкий гребень, протёртость средней части оси
Величину проката определяют с помощью вертикального движка 2 сухаря 3 шаблона 1 по кругу катания...
Неисправности автосцепки, с которыми запрещается постановка вагонов в поезд. Причины саморасцепов ЗАПРЕЩАЕТСЯ: постановка в поезда и следование в них вагонов, у которых автосцепное устройство имеет хотя бы одну из следующих неисправностей:
- трещину в корпусе автосцепки, излом деталей механизма...
Понятие метода в психологии. Классификация методов психологии и их характеристика Метод – это путь, способ познания, посредством которого познается предмет науки (С...
|
Демографияда "Демографиялық жарылыс" дегеніміз не? Демография (грекше демос — халық) — халықтың құрылымын...
Субъективные признаки контрабанды огнестрельного оружия или его основных частей
Переходя к рассмотрению субъективной стороны контрабанды, остановимся на теоретическом понятии субъективной стороны состава преступления...
ЛЕЧЕБНО-ПРОФИЛАКТИЧЕСКОЙ ПОМОЩИ НАСЕЛЕНИЮ В УСЛОВИЯХ ОМС 001. Основными путями развития поликлинической помощи взрослому населению в новых экономических условиях являются все...
|
|









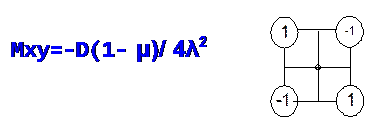
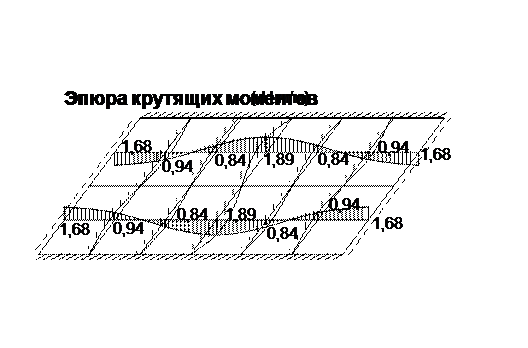
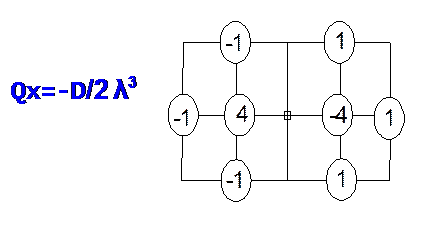



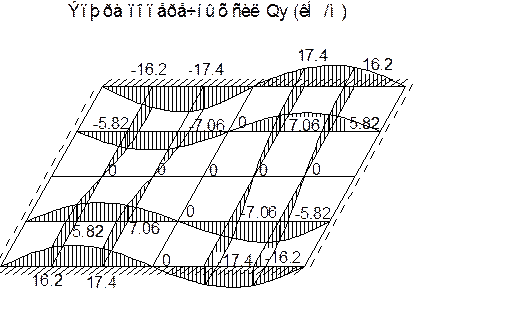
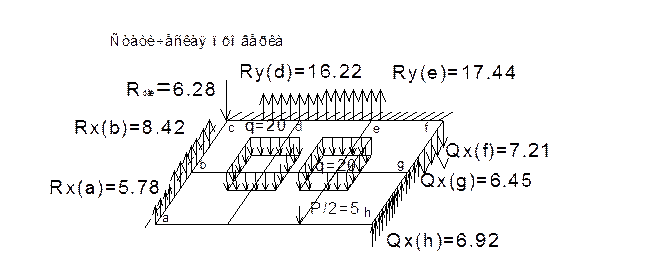


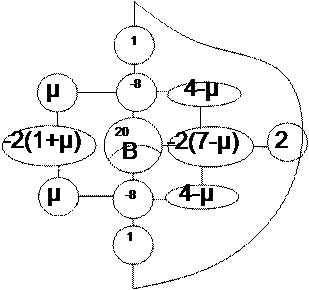


 0
0




