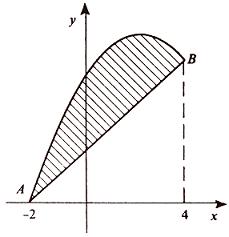
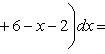Вычислить площадь фигуры, ограниченной линиями .
1. Нечаев В.Я. Социология образования. – М., МГУ, 1992.
2. Сорокин П. А. Человек. Цивилизация. Общество. – М., Политиз 1992.
3. Кравченко А.И. Основы социологии и политологии. – М.: Академический Проект; Фонд “Мир”, 2008.
4. Никитин А.Ф. Большой школьный словарь: обществознание, экономика, право. – М.: АСТ-ПРЕСС, 2006.
5. Обществознание: учеб. для 10-11 кл. общеобразовательных учреждений / под ред. А.Ф. Никитина. – М.: Просвещение, 2006. 6. Обществознание: Пособие-репетитор / под ред. О.С. Белокрыловой, В.И. Филоненко. – Ростов н/Д: Феникс, 2007.
7. Обществознание: учеб.-справ. пособие / под ред. В.В. Барабанова, В.Г. Зарубина. – М.: АСТ: Астрель, 2006.
Вычислить площадь фигуры, ограниченной линиями.
Решение. Находим точки пересечения заданных линий. Для этого решаем систему уравнений:
Для нахождения абсцисс точек пересечения заданных линий решаем уравнение:
Находим: x 1 = -2, x 2 = 4. Итак, данные линии, представляющие собой параболу и прямую, пересекаются в точках A (-2; 0), B (4; 6).
Эти линии образуют замкнутую фигуру, площадь которой вычисляем по указанной выше формуле:
По формуле Ньютона-Лейбница находим:
|

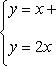
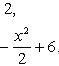

 или
или  .
.