Определить объем тела, ограниченного поверхностью, полученной от вращения эллипса вокруг большой оси a.
Решение.
Учитывая, что эллипс симметричен относительно осей координат, то достаточно найти объем, образованный вращением вокруг оси Ox площади OAB, равной одной четверти площади эллипса, и полученный результат удвоить. Обозначим объем тела вращения через Vx; тогда на основании формулы
Таким образом, искомый объем равен Найти площадь, ограниченную параболами y 2 = 2 px и x 2 = 2 py.
Решение.
Сначала найдем координаты точек пересечения парабол, чтобы определить отрезок интегрирования. Преобразуя исходные уравнения, получаем Отсюда x 4 - 8 p 3 x = x (x 3 - 8 p 3) = x (x - 2 p)(x 2 + 2 px + 4 p 2) = 0. Находим корни уравнений:
Учитывая то факт, что точка A пересечения парабол находится в первой четверти, то пределы интегрирования x = 0 и x = 2 p. Искомую площадь находим по формуле
|
имеем 
, где 0 и a - абсциссы точек B и A. Из уравнения эллипса находим 
. Отсюда
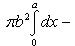
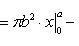
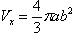. (При вращении эллипса вокруг малой оси b, объем тела равен 
)
и 
. Приравнивая эти значения, получим 
или x 4 - 8 p 3 x = 0.
