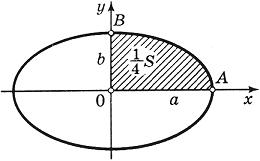
Найти площадь области, ограниченной эллипсом .
Решение.
Из уравнения эллипса для I квадранта имеем
Применим подстановку x = a sin t, dx = a cos t dt. Новые пределы интегрирования t = α; и t = β; определяются из уравнений 0 = a sin t, a = a sin t. Можно положить α; = 0 и β; = π;/2. Находим одну четвертую искомой площади
Отсюда S = πab. Найти площадь фигуры, ограниченной линиями y = - x 2 + x + 4 и y = - x + 1.
Решение. Найдем точки пересечения линий y = - x 2 + x + 4, y = - x + 1, приравнивая ординаты линий: - x 2 + x + 4 = - x + 1 или x 2 - 2 x - 3 = 0. Находим корни x 1 = -1, x 2 = 3 и соответствующие им ординаты y 1 = 2, y 2 = -2.
По формуле площади фигуры получаем
Определить площадь, ограниченную параболой y = x 2 + 1 и прямой x + y = 3.
Решение. Решая систему уравнений
находим абсциссы точек пересечения x 1 = -2 и x 2 = 1.
Полагая y 2 = 3 - x и y 1 = x 2 + 1, на основании формулы
Вычислить площадь, заключенную внутри лемнискаты Бернулли r 2 = a 2cos 2 φ;.
Решение.
В полярной системе координат площадь фигуры, ограниченной дугой кривой r = f (φ;) и двумя полярными радиусами φ;1 = ʅ; и φ;2 = ʆ;, выразится интегралом
В силу симметрии кривой определяем сначала одну четвертую искомой площади
Следовательно, вся площадь равна S = a 2. Вычислить длину дуги астроиды x 2/3 + y 2/3 = a 2/3.
Решение.
Запишем уравнение астроиды в виде (x 1/3)2 + (y 1/3)2 = (a 1/3)2. Положим x 1/3 = a 1/3cos t, y 1/3 = a 1/3sin t. Отсюда получаем параметрические уравнения астроиды x = a cos3 t, y = a sin3 t, (*) где 0 ≤ t ≤ 2 π;. Ввиду симметрии кривой (*) достаточно найти одну четвертую часть длины дуги L, соответствующую изменению параметра t от 0 до π;/2. Получаем dx = -3 a cos2 t sin t dt, dy = 3 a sin2 t cos t dt. Отсюда находим
Интегрируя полученное выражение в пределах от 0 до π;/2, получаем
Отсюда L = 6 a. Найти площадь, ограниченную спиралью Архимеда r = aφ; и двумя радиусами-векторами, которые соответствуют полярным углам φ;1и φ;2 (φ;1 < φ;2).
Решение.
Площадь, ограниченная кривой r = f (φ;) вычисляется по формуле Таким образом, получаем
Из (*) следует, что площадь, ограниченная полярной осью и первым витком спирали Архимеда (φ;1 = 0; φ;2 = 2 π;):
Аналогичным образом находим площадь, ограниченную полярной осью и вторым витком спирали Архимеда (φ;1 = 2 π;; φ;2 = 4 π;):
Искомая площадь равна разности этих площадей
Вычислить объем тела, полученного вращением вокруг оси Ox фигуры, ограниченной параболами y = x 2 и x = y 2.
Решение.
Решим систему уравнений
и получим x 1 = 0, x 2 = 1, y 1 = 0, y 2 = 1, откуда точки пересечения кривых O (0; 0), B (1; 1). Как видно на рисунке, искомый объем тела вращения равен разности двух объемов, образованных вращением вокруг оси Ox криволинейных трапеций OCBA и ODBA:
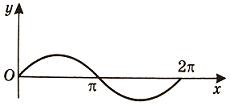
Вычислить площадь, ограниченную осью Ox и синусоидой y = sin x на отрезках: а) [0, π;]; б) [0, 2 π;].
Решение.
а) На отрезке [0, π;] функция sin x сохраняет знак, и поэтому по формуле
б) На отрезке [0, 2 π;], функция sin x меняет знак. Для корректного решения задачи, необходимо отрезок [0, 2 π;] разделить на два [0, π;] и [ π;, 2 π;], в каждом из которых функция сохраняет знак. По правилу знаков, на отрезке [ π;, 2 π;] площадь берется со знаком минус. В итоге, искомая площадь равна
|


 . Отсюда по формуле
. Отсюда по формуле  получаем
получаем







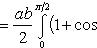
















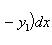 получаем
получаем
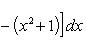








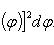















 , где α; и β; - пределы изменения полярного угла.
, где α; и β; - пределы изменения полярного угла.

 (*)
(*)

















 , полагая y = sin x, находим
, полагая y = sin x, находим














