Применяя метод Остроградского вычислить интеграл .
Решение. Представим исходный интеграл в виде
Дифференцируя и приводя к общему знаменателю, получаем тождество 1 ≡ (x 4 - 1)(7 Ax 6 + 6 Bx 5 + 5 Cx 4 + 4 Dx 3 + 3 Ex 2 + 2 Fx + G) – - 8 x 3(Ax 7 + Bx 6 + Cx 5 + Dx 4 + Ex 3 + Fx 2 + Gx + H) + + (x 8 - 2 x + 1)(Kx 3 + Lx 2 + Mx + N). Сравнивая коэффициенты при одинаковых степенях x в обеих частях равенства, имеем
Решая систему, получаем A = B = D = E = F = H = K = L = M = 0, C = 7/32, G = -11/32, N = 21/32. Таким образом,
Вычисляя последний интеграл, окончательно получаем
Примеры. Необходимо иметь в виду простейшие преобразования дифференциала
j'(x)dx=dj(x)
Интегрирование путем введения новой переменной (метод подстановки) основано на формуле
где х = j(t) - дифференцируемая функция переменной t. Примеры. Найти интеграл Тригонометрические подстановки 1) Если интеграл содержит радикал
Далее сответственно Пример. Найти Если u = j(x) и v = y(х) - дифференцируемые функции, то
Эта формула применяется в случае, когда подынтегральная функция представляет произведение алгебраической и трансцендентной функции. Примеры. °. Интеграл вида
путем дополнения квадратного трехчлена до полного квадрата по формуле
сводится к одному из двух интегралов
где u = х + k. 2°. Интеграл
сводится к интегралам вида (8.1) или (8.2) и интегралу
3°. Интеграл
сводится к одному из интегралов:
сводится к одному из двух интегралов
сводится к разобранным выше интегралам. Примеры. 6°. Интегралы вида
с помощью обратной подстановки Пример. 1°. Интегралы вида
находятся с помощью тригонометрических формул
где m и n - четные числа находятся с помощью формул понижения степени
Если хотя бы одно из чисел m или n - нечетное, то полагают (пусть m = 2k + 1)
В частности, к этому случаю сводятся интегралы
4°. Интегралы вида
где R - рациональная функция от sinx и cosx, приводятся к интегралам от рациональных функций новой переменной с помощью подстановки
Задача 1. Вычислить неопределенные интегралы.
Задача 4. Вычислить определенные интегралы.
Задача 7. Найти неопределенные интегралы. Задача 9. Вычислить определенные интегралы. Задача 12. Вычислить определенные интегралы.
Задача 15. Вычислить площади фигур, ограниченных линиями, заданными уравнениями. Задача 17. Вычислить длины дуг кривых, заданных уравнениями в прямоугольной системе координат. Задача 19. Вычислить длины дуг кривых, заданных уравнениями в полярных координатах. Задача 20. Вычислить объемы тел, ограниченных поверхностями. Цилиндр наполнен газом пол атмосферным давлением (103,3 кПа). Считая газ идеальным, определить работу (в джоулях) при изотермическом сжатии газа поршнем, переместившемся внутрь цилиндра на У к а з а н и е. Уравнение состояния газа
|























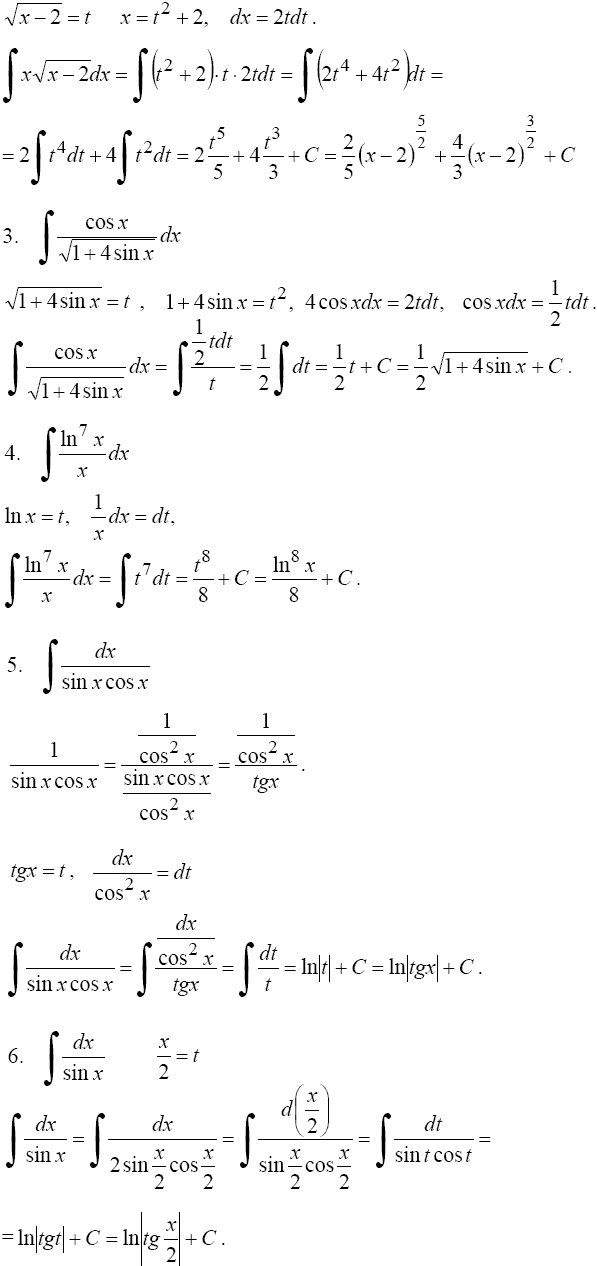






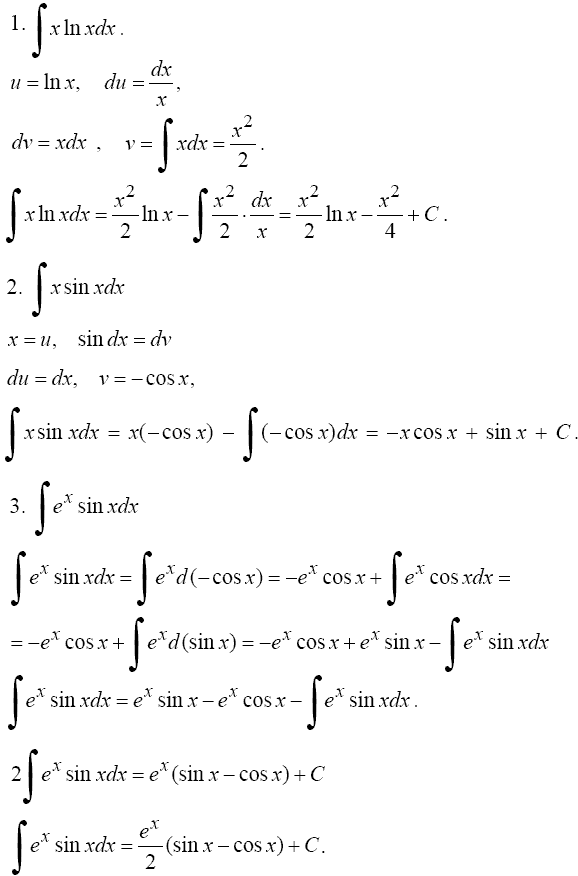



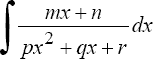



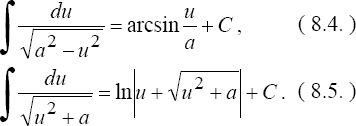























 Задача 2. Вычислить определенные интегралы.
Задача 2. Вычислить определенные интегралы.  Задача 3. Найти неопределенные интегралы.
Задача 3. Найти неопределенные интегралы. 
 Задача 5. Найти неопределенные интегралы.
Задача 5. Найти неопределенные интегралы.  Задача 6. Найти неопределенные интегралы.
Задача 6. Найти неопределенные интегралы. 
 Задача 8. Вычислить определенные интегралы.
Задача 8. Вычислить определенные интегралы. 
 Задача 10. Вычислить определенные интегралы.
Задача 10. Вычислить определенные интегралы.  Задача 11. Вычислить определенные интегралы.
Задача 11. Вычислить определенные интегралы. 
 Задача 13. Найти неопределенные интегралы.
Задача 13. Найти неопределенные интегралы.  Задача 14. Вычислить площади фигур, ограниченных графиками функций.
Задача 14. Вычислить площади фигур, ограниченных графиками функций. 
 Задача 16. Вычислить площади фигур, ограниченных линиями, заданными уравнениями в полярных координатах.
Задача 16. Вычислить площади фигур, ограниченных линиями, заданными уравнениями в полярных координатах. 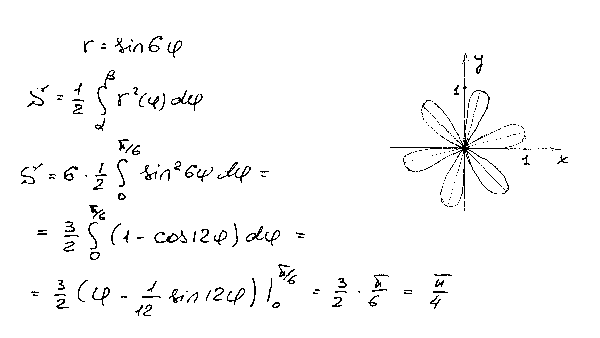 Задача 21. Вычислить объемы тел, образованных вращением фигур, ограниченных графиками функций. Ось вращения
Задача 21. Вычислить объемы тел, образованных вращением фигур, ограниченных графиками функций. Ось вращения  .
. 
 Задача 18. Вычислить длины дуг кривых, заданных параметрическими уравнениями.
Задача 18. Вычислить длины дуг кривых, заданных параметрическими уравнениями. 


 м (рис. 3).
м (рис. 3). , где
, где  - давление,
- давление,  - объем.
- объем. 




