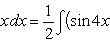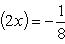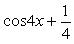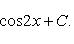Найти интеграл . Разложим исходный интеграл на сумму двух интегралов:
Решение. Разложим исходный интеграл на сумму двух интегралов:
Чтобы вычислить первый из этих интегралов воспользуемся тем, что
(и тем самым, множитель x «подведем под знак дифференциала»), и сделаем замену переменной: t = 3 - x 2. Получаем:
Полученный интеграл является табличным: Применяя эту формулу при Возвращаясь к переменной x, получаем:
Аналогично вычисляем интеграл
В итоге, получаем:
Вычислить интеграл.
Решение.
Найти интеграл.
Решение. Применим формулу интегрирования по частям Получаем:
Снова применим формулу интегрирования по частям, положив u = ln x, dv = xdx. Тогда Тогда
Таким образом, Найти интеграл.
Решение. Учитывая, что
|


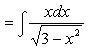

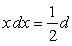





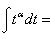
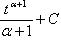
 , имеем:
, имеем: 
 .
.












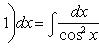



 . Положим u = ln2 x, dv = xdx, тогда
. Положим u = ln2 x, dv = xdx, тогда 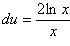
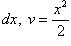 .
.
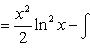


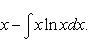

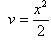 .
.

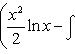








 .
.

 , получаем:
, получаем: