Найти интеграл .
Решение. Известно, что cos 2 x = 2cos2 x - 1. Произведем замену t = cos x, тогда получим
Подинтегральное выражение мы привели к дробно-рациональному виду. Теперь выделим целую часть и разложим на простейшие дроби:
Находим далее
Теперь вернемся к старой переменной x:
Найти интеграл.
Решение.
Найти интеграл.
Решение. Известно, что
т. е. иррациональности в подинтегральном выражении исчезают. Так как: Подставляя найденные выражения в исходный интеграл, находим:
Для нахождения интеграла выделим целую часть подинтегральной функции:
Интегрируя каждое из слагаемых, получаем
Вернемся к старой переменной. Так как
|
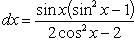
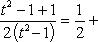
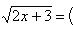
. Наименьшим общим кратным знаменателей дробей 
является 6. Поэтому, если применить подстановку 2 x + 3 = t 6, тогда:
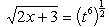
, то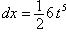 
.
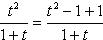
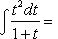
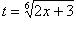, то получаем
