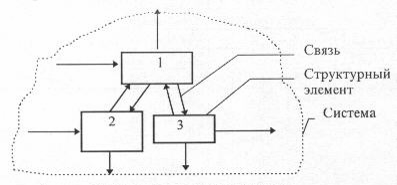
Структурные схемы

Формирование структуры является частью решения общей задачи описания системы. Структура выявляет общую конфигурацию системы, а не определяет систему в целом.

Если изобразить систему как совокупность блоков, осуществляющих некоторые функциональные преобразования, и связей между ними, то получим структурную схему, в обобщенном виде описывающую структуру системы. Под блоком обычно понимают, особенно в технических системах, функционально законченное и оформленное в виде отдельного целого устройство. Членение на блоки может осуществляться исходя из требуемой степени детализации описания структуры, наглядности отображения в ней особенностей процессов функционирования, присущих системе. Помимо функциональных, в структурную схему могут включаться логические блоки, позволяющие изменять характер функционирования в зависимости от того, выполняются или нет некоторые заранее заданные условия.

Структурные схемы наглядны и вмещают в себя информацию о большом числе структурных свойств системы. Они легко поддаются уточнению и конкретизации, в ходе которой не надо изменять всю схему, а достаточно заменить отдельные ее элементы структурными схемами, включающими не один, как раньше, а несколько взаимодействующих блоков.

Однако, структурная схема — это еще не модель структуры. Она с трудом поддается формализации и является скорее естественным мостиком, облегчающим переход от содержательного описания системы к математическому, чем действительным инструментом анализа и синтеза структур.

Рис. — Пример структурной схемы

Графы

Отношения между элементами структуры могут быть представлены соответствующим графом, что позволяет формализовать процесс исследования инвариантных во времени свойств систем и использовать хорошо развитый математический аппарат теории графов.

Определение. Графом называют тройку G=(M, R, P), где М — множество вершин, R — множество ребер (или дуг графа), Р — предикат инцидентности вершин и ребер графа. Р(x, y, r) = 1 означает, что вершины x,y ∈ M инцидентны (связаны, лежат на) ребру графа r ∈ R.

Для того чтобы облегчить работу с графом, вершины его обычно нумеруют. Граф с пронумерованными вершинами называется отмеченным.

Каждое ребро графа связывает две вершины, называемые в этом случае смежными. Если граф отмечен, то ребро задается парой (i,j), где i и j — номера смежных вершин. Очевидно, что ребро (i,j) инцидентно вершинам i и j, и обратно.

Если все ребра графа заданы упорядоченными парами (i,j), в которых порядок расположения смежных вершин имеет значение, то граф называется ориентированным. Неориентированный граф не содержит ориентированных ребер. В частично ориентированном графе ориентированы не все ребра.

Геометрически графы изображают в виде диаграмм, на которых вершины отображаются точками (окружностями, прямоугольниками), а ребра — отрезками, соединяющими смежные вершины. Ориентированное ребро задают отрезком со стрелкой.

Использование диаграмм настолько распространено, что обычно, говоря о графе, представляют себе именно диаграмму графа.

Если ребра графа имеют некоторые числовые характеристики связи, то такие графы называются взвешенными. В этом случае матрица инцидентности содержит веса соответствующих связей, знак перед числом определяет направление ребра.

Важной характеристикой структурного графа является число возможных путей, по которым можно пройти от одной вершины к другой. Чем больше таких путей, тем совершеннее структура, но тем она избыточнее. Избыточность обеспечивает надежность структуры. Например, разрушение 90% нервных связей головного мозга не ощущается и не влияет на поведение. Может существовать и бесполезная избыточность, которая в структурном графе изображается в виде петель.