Теория и расчет
Для системы координат, которая вращается с угловой скоростью
Сила тяжести уравновешивается реакцией дорожки. Тележка находится в состоянии покоя в подвижной системе координат, которая вращается с постоянной угловой скоростью
Рис. 3: Зависимость центробежной силы от массы
Рис. 4: Определение зависимости центробежной силы от угловой скорости
Поэтому в выражении (1) остается только центробежная сила и уравновешивающая сила
Так как
Используя функцию
и анализируя прямую на Рис. 4, получаем коэффициент
Замечание
Изменение показаний динамометра, который используется для измерения центробежной силы, происходит согласно закону Гука:
где Поскольку центробежная сила также прямо пропорциональна
то следует рассмотреть случаи: 1. Устойчивое состояние для 2. Безразличное состояние для 3. Неустойчивое состояние для
В целях безопасности неустойчивое и безразличное состоянии в данном эксперименте не рассматривается.
Рис. 5: Зависимость центробежной силы от радиуса.
|

 уравнение движения материальной точки (с массой
уравнение движения материальной точки (с массой  и радиус-вектором
и радиус-вектором  ) имеет вид:
) имеет вид: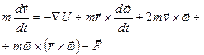 (1)
(1) (
(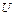 = 0;
= 0; 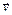 = const = 0;
= const = 0; 


 , определяемая при помощи динамометра:
, определяемая при помощи динамометра: .
. , то
, то . (2)
. (2)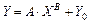 ,
, = 2,053
= 2,053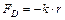 ,
, жесткость пружины.
жесткость пружины.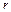 :
: ,
,

 .
.



