Вывод остатка
В результате всех действий получаем значения коэффициентов регрессии:
Полученное уравнение описывает зависимость производительности труда от фондовооруженности и % прибыли. 2.4. Экономический анализ полученных результатов · Коэффициент множественной корреляции R характеризует тесноту связи между результатирующим показателем и независимыми переменными. В моем случае он равен 0,991885095 (R приближено к 1) показывает, что связь между Y с одной стороны и аргументами x1, x2 с другой стороны является функциональной и линейной. · Значение множественного коэффициента детерминации (R²), равное 0,983836042 свидетельствует о значительном влиянии включенных в модель факторов на результатирующий показатель. · Стандартная ошибка – это допустимое отклонение теоретического результатирующего фактора от фактического. · Уровень значимости F характеризует среднюю вероятность принятия нулевой гипотезы по уравнению в целом. · Коэффициентыпредставляют собой значения свободного члена уравнения регрессии и коэффициентов уравнения регрессии. Коэффициенты уравнения регрессии: Коэффициент a = 17,79. Формально a – значение Y при x · Р-значение – это вероятность принятия нулевой гипотезы по каждому коэффициенту уравнения регрессии. · Нижние 95% и верхние 95% - это уровень доверия, которому соответствует 5%-ный уровень значимости, то есть вероятности ошибки. Значения этих показателей определяют минимальный и максимальный уровень коэффициентов, используемых в уравнении при 5%-ном уровне значимости. · t-статистиканаходится как отношение столбца «Коэффициенты» к столбцу «Стандартная ошибка». На основании этих характеристик можно сделать вывод о том, что модель достаточно точна, адекватна и пригодна для прогнозирования. Корреляционная связь, описанная уравнением
2.5. Четыре обязательных свойства «Остатков» Для того чтобы полученное уравнение регрессии было адекватным необходимо, чтобы остаточная компонента удовлетворяла следующим свойствам: 1. случайность колебаний уровней остаточной последовательности; 2. соответствие распределения случайной компоненты нормальному закону распределения: 3. равенство нулю математического ожидания случайной компоненты; 4. независимость значений уровней случайной компоненты. Рассмотрим способы проверки этих свойств остаточной последовательности. 2.6. Проверка выполнения свойств остаточной компоненты 2 .6.1 Проверка случайности колебаний уровней остаточной последовательности Данная проверка означает проверку гипотезы о правильности выбора уравнения регрессии. Для исследования случайности отклонений от уравнения регрессии находятся разности Характер этих отклонений изучается с помощью ряда непараметрических критериев. Одним из таких критериев является критерий серий, основанный на медиане выборки. Ряд из величин Последовательность подряд идущих «+» и «-» называется серией. Для того чтобы последовательность Обозначим протяженность самой длинной серии K
Где квадратные скобки означают целую часть числа. Если хотя бы одно из этих неравенств нарушается, то гипотеза о случайном характере отклонений уровней ряда от теоретических уровней отвергается и модель признается неадекватной. Нами были проделаны соответствующие вычисления по нахождению 2<[3.31g (20+1)]; 2<4 14>[1/2(20+1-1.96 20-1]; 14>6 2.6.2. Проверка соответствия распределения случайной компоненты нормальному закону распределения Данная проверка производится обычно приближенно с помощью нахождения показателей асимметрии Для оценки соответствия выбранной совокупности данных нормальному закону распределения используется так называемая оценка показателей эксцесса и асимметрии. В качестве оценки асимметрии используется формула:
Оценка эксцесса:
Где
То гипотеза о нормальном распределении случайной компоненты принимается. Если:
То гипотеза о нормальном распределении отвергается и модель признается не адекватной. Мы произвели необходимые вычисления по нахождению суммы во второй, третьей и четвертой степенях, следовательно, используя найденные значения, произведем согласно вышеприведенным формулам необходимые вычисления:
0,158018886 0,761076154
Теперь проверим выполнение соответствующих неравенств:
│-0,153357086│<1,5*0,472866244
│-0,153357086│<0,709299366 │-0,3739508│<1,141614231
Неравенства выполняются одновременно, следовательно, гипотеза о нормальном распределении случайной компоненты принимается. 2.6.3.Проверка равенства математического ожидания случайной компоненты нулю Проверка осуществляется на основе t – критерия Стьюдента. Расчетное значение этого критерия находится по формуле:
Где
Если расчетное значение t меньше табличного значения по статистике Стьюдента с заданным уровнем значимости а и числом степеней свободы k=n-1, и гипотеза о равенстве 0 математического ожидания случайной последовательности принимается и модель признается адекватной.
2.6.4. Проверка независимости значений уровней случайной компоненты Данная проверка осуществляется для выявления существующей автокорреляции остаточной последовательности, то есть зависимости последующего значения отклонения от предыдущего. Эта проверка может производится по ряду критериев. Наиболее распространенным является критерий Дарбин-Уотсона. Расчетное значение этого критерия находится по формуле:
Подставив все значения в данную формулу, мы получили: d=0,132198173
Расчетное значение d – критерия в интервале от 2 до 4 свидетельствует об отрицательной связи. В этом случае его надо преобразовать по формуле: d’=4-d Расчетное значение критерия d или d’ сравнивается с верхним d d= 2,235917417 d'= 1,764082583 Поскольку расчетное значение критерия d больше верхнего табличного значения d2, то модель адекватна. Если расчетное значение d меньше табличного d Если d находится между значениями d Таким образом, гипотеза о независимости уровней остаточной последовательности принимается.
|
= 0,34, 
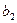=10,32- показывают среднее изменение результата с изменением факторов на одну единицу.
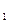и x 
= 0. Если признак фактор X не имеет и не может иметь нулевого значения, то трактовка свободного члена а не имеет смысла. Параметр а может не иметь экономического содержания. Интерпретировать можно только знак при параметре а. Если а<0, то относительное изменение результата происходит быстрее, чем изменение фактора.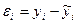
.
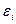располагают в порядке возрастания их значений и находят медиану 
, полученного вариационного ряда, то есть срединной значение при n нечетном или среднюю арифметическую при 2-х соседних срединных значений при четном n. Возвращаясь к исходной последовательности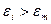 
и знак «-», если 
. Следовательно, значение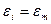 
. Таким образом, получается последовательность, состоящая из «+» и «-», общее число которых не превосходит n.
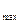,а общее число серий через 
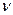. Выборка признается случайной, если выполняются следующие неравенства для 5%-го уровня значимости: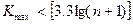
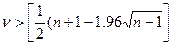
и эксцесса 
. Так как изучаемые ряды, как правило, не очень велики, это производится на основании сравнения найденных показателей с теоретическими. При нормальном распределении некоторой генеральной совокупности показатели асимметрии и эксцесса должны быть равны 0. При конечной выборки из генеральной совокупности показатели асимметрии и эксцесса имеют отклонения и 0.
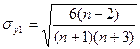
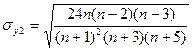
и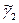 
– выборочные характеристики асимметрии и, соответственно, эксцесса, а 
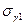и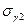 
их среднеквадратические ошибки. Если одновременно выполняются неравенства: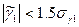
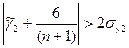
-0,2499 0,472866244
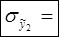
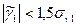
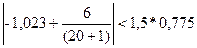
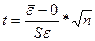
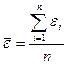
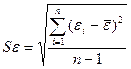
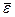– среднеарифметическое значение;
- стандартное среднеквадратическое отклонение для этой последовательности.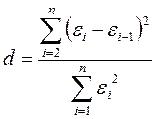
и нижним d 
критическими значениями статистики Дарвина-Уотсона.
