Проверка закона распределенияВ первую очередь представляет интерес закон распределения, особенно для переменных, относящихся к интервальной шкале и шкале отношений. Чаще всего при этом ставится вопрос, подчиняются ли значения переменных нормальному распределению. Именно от этого практически всегда зависит выбор соответствующих аналитических тестов. Многочисленные методы, с помощью которых обрабатываются переменные, относящиеся к интервальной шкале, исходят из гипотезы, что их значения подчиняются нормальному распределению. При таком распределении большая часть значений группируется около некоторого среднего значения, по обе стороны от которого частота наблюдений равномерно снижается.
Как видим у нас получились две абсолютно идентичные гистограммы. Но на правой диаграмме нанесена кривая нормального распределения (Колокол Гаусса). Для этого в диалоговом окне Histogram установил флажок Displaynormalcurve.
Реальное распределение в большей или меньшей степени отклоняется от этой идеальной кривой. Выборки, строго подчиняющиеся нормальному распределению, на практике, как правило, не встречаются. Поэтому почти всегда необходимо выяснить, можно ли реальное распределение считать нормальным и насколько значительно заданное распределение отличается от нормального. Перед применением любого метода, который предполагает существование нормального распределения, наличие последнего нужно проверять в первую очередь. Классическим примером статистического теста, который исходит из гипотезы о нормальном распределении, можно назвать t-тест Стьюдента, с помощью которого сравнивают две независимые выборки. Если же данные не подчиняются нормальному распределению, следует использовать соответствующий непараметрический тест, в случае двух независимых выборок — U-тест Манна и Уитни. В этом отношении самым распространенным и рекомендуемым является графическое изображение распределения данных в форме гистограммы и наложенным колоколом Гаусса (эта проверка была рассмотрена выше). 2.2 Тест Колмогорова – Смирнова. Объективная проверка на нормальное распределение проводится с помощью подходящего статистического критерия (теста Колмогорова-Смирнова). При помощи этого теста по выбору можно проверить, соответствует ли реальное распределение переменной нормальному, равномерному, экспоненциальному распределению или распределению Пуассона. Разумеется, самым распространённым видом проверки является проверка наличия нормального распределения. Выберите в меню Analyze (Анализ) NonparametricTests (Непараметрические тесты) 1-Sample KS (К-С одной выборки). В результате получаем таблицу с анализом на предмет соответствия переменной vozrast нормальному закону.
Расшифровка таблицы ОneSampleКolomgorov-SmirnovTest
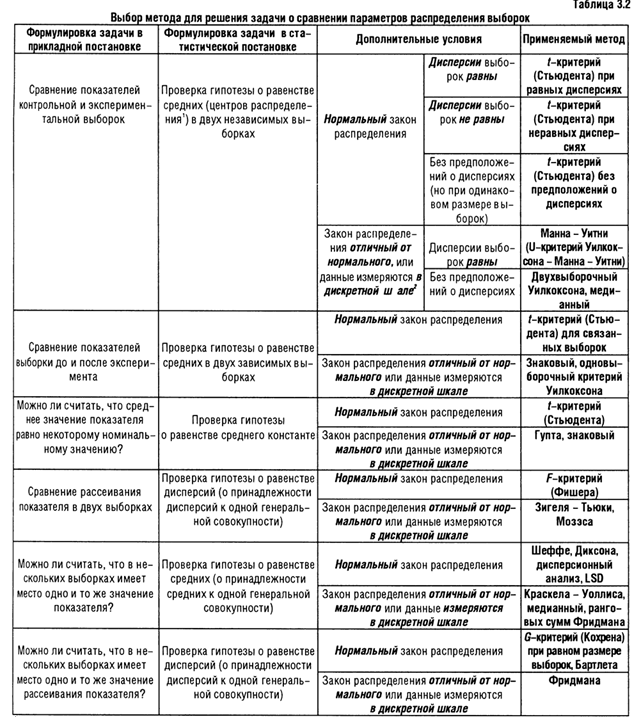
a. Test distribution is Normal. (Тестируемое распределение является нормальным распределением.) b. Calculatedfromdata. (Рассчитано исходя из исходных данных.) Полученные результаты включают: · среднее значение и стандартное отклонение · промежуточные результаты, полученные в результате теста Колмогорова-Смирнова · вероятность ошибки р. Отклонение от нормального распределения считается существенным при значении р< 0,05; в этом случае для соответствующих переменных следует применять непараметрические тесты. В рассматриваемом примере (значение р = 0,046), то есть вероятность ошибки является не значимой; поэтому значения переменной достаточно хорошо подчиняются нормальному распределению. Провести исследование 2-3 переменных (bolidlit и rvotdlit) с использованием Колокола Гаусса и теста Колмогорова-Смирнова на предмет их соответствия нормальному распределению. Результаты исследования переменных с их графиками и таблицами представить в отчете. Необходимость исследование на нормальность распределения обусловлена прежде всего тем, что существуют различные подходы к решению статистических задач в зависимости от того под какой закон распределения мы можем подвести ту или иную случайную величину. В таблице 3.2 приведены примеры задач по статистической обработке данных имеющих различные функции распределения и соответственно свои способы решения задач.
2.3 Анализ данных без группирующей переменной
Поначалу вас может смутить то, что в этом диалоговом окне проводится различие между зависимыми переменными и факторами. Это означает, что можно выполнять анализ раздельно по группам наблюдений. В этом случае анализируемой переменной будет зависимая переменная, а группирующей переменной — фактор. Если же такой раздельный анализ проводить не требуется, список факторов не используется. Мы рассмотрим для начала такой анализ данных, который не должен производиться по группам раздельно Проведем анализ возраста пациентов.
|
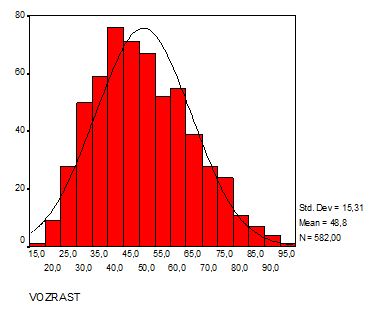
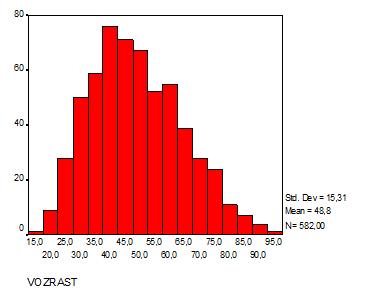2.1 Построение диаграммы. В качестве примера рассмотрим нормальное распределение возраста, которое строится по данным исследований jazvasi.sav с помощью команд меню Graphs (Графы) Histogramm... (Гистограмма) (см. рис.). В начале строим гистограмму без установки флажка Display normal curve в диалоговом окне Histogram. Изучите распределение, дайте толкование параметров Std.Dev, Mean. Затем аналогичным способом но с установкой флажка строим другую гистограмму.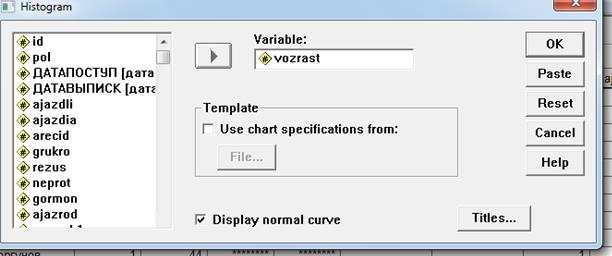
Появится диалоговое окно OneSampleКolomgorov-SmirnovTest (Тест Колмогорова-Смирнова для одной выборки) (см. рис.). Вводим переменную vozrast и нажимаем ОК.
Опять обратимся к переменной Возраст в jazvasi.sav. Перейдите к исследованию данных, выбрав команды меню Analyze (Анализ) DescriptiveStatistics (Дескриптивныестатистики) Explore... (Исследовать) Откроется диалоговое окно Explore.
