Пятый постулат Евклида. Неевклидова геометрия.

4.4.40. Помещения аккумуляторных батарей, в которых производится заряд аккумуляторов при напряжении более 2,3 В на элемент, должны быть оборудованы стационарной принудительной приточно-вытяжной вентиляцией.

Для помещений аккумуляторных батарей, работающих в режиме постоянного подзаряда и заряда при напряжении до 2,3 В на элемент, должно быть предусмотрено применение стационарных или инвентарных устройств принудительной приточно-вытяжной вентиляции на период формовки батарей и контрольных перезарядов.

Требуемый объем свежего воздуха V, м³/ч, определяется по формуле:

 

V =0,07I_зарn,

 

где I_зар - наибольший зарядный ток, А; п - количество элементов аккумуляторной батареи; при этом концентрация серной кислоты в воздухе помещения аккумуляторной батареи должна быть не более указанной в СН 245-71* «Санитарные нормы проектирования промышленных предприятий» Госстроя СССР.

Кроме того, для вентиляции помещений аккумуляторных батарей должна быть выполнена естественная вытяжная вентиляция, которая обеспечивает не менее чем однократный обмен воздуха в час. В тех случаях, когда естественная вентиляция не может обеспечить требуемую кратность обмена воздуха, должна применяться принудительная вытяжная вентиляция.

4.4.41. Вентиляционная система помещений аккумуляторной батареи должна обслуживать только аккумуляторные батареи и кислотную. Выброс газов должен производиться через шахту, возвышающуюся над крышей здания не менее чем на 1,5 м. Шахта должна быть защищена от попадания в нее атмосферных осадков. Включение вентиляции в дымоходы или в общую систему вентиляции здания запрещается.

4.4.42. При устройстве принудительной вытяжной вентиляции вентилятор должен иметь взрывобезопасное исполнение.

4.4.43. Отсос газов должен производиться как из верхней, так и из нижней части помещения со стороны, противоположной притоку свежего воздуха.

Если потолок имеет выступающие конструкции или наклон, то должна быть предусмотрена вытяжка воздуха соответственно из каждого отсека или из верхней части пространства под потолком.

Расстояние от верхней кромки верхних вентиляционных отверстий до потолка должно быть не более 100 мм, а от нижней кромки нижних вентиляционных отверстий до пола - не более 300 мм.

Поток воздуха из вентиляционных каналов не должен быть направлен непосредственно на поверхность электролита аккумуляторов.

Металлические вентиляционные короба не должны располагаться над открытыми аккумуляторами.

Применение инвентарных вентиляционных коробов в помещениях аккумуляторных батарей не допускается.

Скорость воздуха в помещениях аккумуляторных батарей и кислотных при работе вентиляционных устройств должна соответствовать требованиям СН 245-71*.

4.4.44. Температура в помещениях аккумуляторных батарей в холодное время на уровне расположения аккумуляторов должна быть не ниже +10 °С.

На подстанциях без постоянного дежурства персонала, если аккумуляторная батарея выбрана из расчета работы только на включение и отключение выключателей, допускается принимать указанную температуру не ниже 0 °С.

4.4.45. Отопление помещения аккумуляторной батареи рекомендуется осуществлять при помощи калориферного устройства, располагаемого вне этого помещения и подающего теплый воздух через вентиляционный канал. При применении электроподогрева должны быть приняты меры против заноса искр через канал.

При устройстве парового или водяного отопления оно должно выполняться в пределах помещения аккумуляторной батареи гладкими трубами, соединенными сваркой. Фланцевые соединения и установка вентилей запрещаются.

4.4.46. На электростанциях, а также на подстанциях, оборудованных водопроводом, вблизи помещения аккумуляторной батареи должны быть установлены водопроводный кран и раковина. Над раковиной должна быть надпись: «Кислоту и электролит не сливать».

 

 

Пятый постулат Евклида. Неевклидова геометрия.

 

Работу выполнил

Митрофанов Артем, 10 «А» класс

 

Научный руководитель

Сукова Надежда Иларьевна,

учитель математики

 

Архангельск

Оглавление

 

ВВЕДЕНИЕ 3

ОСНОВНАЯ ЧАСТЬ 5

1 Попытки доказательства пятого постулата Евклида 5

2 Опровержение пятого постулата Евклида 7

3 Основы геометрии Лобачевского 8

4 Сферическая геометрия 10

ЗАКЛЮЧЕНИЕ 12

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 13

ПРИЛОЖЕНИЕ 14

 

 

Введение

 

«Начала» Евклида на протяжении более двух тысяч лет подвергались тщательному изучению. Имеется огромная литература, содержащая комментарии к «Началам». Уже древние комментаторы заметили, что «Начала» содержат существенные недостатки, в связи с этим предпринимались попытки их устранения. Особое внимание критиковавших «Начала» Евклида привлекал к себе V постулат:

Если две прямые, лежащие в одной плоскости, пересечены третьей и если сумма внутренних односторонних углов меньше двух прямых углов, то эти прямые пересекутся с той стороны, где это имеет место.

V постулат занимает в системе постулатов «Начал» особое положение в силу ряда глубоких соображений. Прежде всего, обращает на себя внимание то обстоятельство, что утверждение, содержащееся в V постулате, не имеет столь простого и очевидного характера, какой имеют прочие постулаты. Во-вторых, формулировка V постулата носит довольно сложный и громоздкий характер. И наконец, третья особенность заключается в весьма своеобразном использовании Евклидом этого постулата.

В то время, как все остальные постулаты используются им с самого начала, при изложении первых теорем, V постулат применяется впервые лишь в доказательстве 29-го предложения. Таким образом, применение V постулата в «Началах» Евклида резко разграничивает геометрические предложения на две категории: на предложения, доказываемые без помощи V постулата; и на предложения, которые не могут быть доказаны без его использования.

Изложенные особенности V постулата имели большое значение для последующего развития геометрии. Исследователи, жившие после Евклида, и комментаторы «Начал», рассматривали V постулат, как предложение, которое не следует помещать среди постулатов, а необходимо доказать как теорему. Они были убеждены в его доказуемости. Поэтому усилия многих поколений математиков были направлены на то, чтобы доказать V постулат при помощи остальных постулатов и тем самым свести его в разряд теорем. В этом и заключалась проблема V постулата Евклида.

Решением этой проблемы занимались многие математики, в том числе: Посидоний (I в. до н. э.), Птолемей (III в. до н. э.), Прокл (410 – 475 гг), Насир-Эддин (1201 – 1274 гг.), Д. Валлис (1616 – 1703 гг.), Ламберт (1728 – 1777 гг.), Лежандр (1752 – 1833 гг.), Гаусс (1777 – 1855 гг.), И. Больяи (1802 – 1860 гг.). Все они неизменно оканчивались неудачей. Авторы доказательств в своих рассуждениях использовали явным или скрытым образом наглядно очевидные предложения, которые при тщательном анализе оказывались предложениями эквивалентными самому постулату.

Насколько велик труд, затраченный на исследования, связанные с проблемой доказательства V постулата, можно судить по тому, что известно около 250 серьёзных сочинений, посвящённых теории параллельности и не достигших поставленной цели. Однако, несмотря на безрезультатность и тщетность всех попыток доказательства V постулата, они всё же не были бесполезны. В результате этих многовековых поисков были выявлены логические зависимости между некоторыми важными геометрическими предложениями и, в частности, были открыты предложения, эквивалентные V постулату. Например, в современной школьной практике V постулат известен, как аксиома параллельных Плейфера: «Через точку, лежащую вне данной прямой, можно провести только одну прямую, параллельную данной».

В данной работе будут рассмотрены попытки доказательства пятого постулата Евклида, его опровержение и основы неевклидовой геометрии, своим появлением обязанной пятому постулату.

Цель работы: доказать справедливость существования неевклидовых геометрий и показать их равнозначность с геометрией евклидовой.

 

 

Основная часть

 

1 Попытки доказательства пятого постулата Евклида

Возможно, что уже сам Евклид пытался доказать постулат о параллельных. В пользу этого говорит то обстоятельство, что первые 28 предложений “Начал” не опираются на V постулат. Евклид как бы старался отодвинуть применение этого постулата до тех пор, пока использование его не станет настоятельно необходимым.

Вера в незыблемость «Начал Евклида» была такова, что в течение 2000 лет никто из геометров не сомневался в справедливости пятого постулата Евклида, и все усилия самых знаменитых геометров, интересовавшихся этим вопросом, были направлены на отыскание доказательства этого постулата.

Одни математики старались доказать постулат о параллельных, применяя только другие постулаты и те теоремы, которые можно вывести из последних, не используя сам V постулат. Все такие попытки оказались неудачными. Их общий недостаток в том, что в доказательстве неявно применялось какое-нибудь предположение, равносильное доказываемому постулату.

Так, например, Посидоний (I век до нашей эры) основывал свое доказательство на определении параллельных, как линий, равноотстоящих друг от друга; а Прокл (410-480 г.) принимал за очевидное, что расстояние между параллельными конечно.

Птоломей (II век нашей эры) основал свое доказательство на допущении, что две прямые параллельны в одном направлении, то они параллельны и в другом;

Другие предлагали по-новому определить параллельные прямые или же заменить V постулат каким-либо, по их мнению, более очевидным предложением. Так, например, в XI веке Омар Хайям ввел вместо V постулата “принцип”, согласно которому две лежащие в одной плоскости сходящиеся прямые пересекаются и не могут расходиться в направлении схождения. С помощью этого принципа Хайям доказывает, что в четырехугольнике ABCD, в котором углы при основании А и В – прямые и стороны АС, ВD равны, углы С и D так же прямые, а из этого предложения о существовании прямоугольника выводится V постулат. Рассуждения Хайяма получили оригинальное развитие в XIII веке у Насирэдинна ат-Туси, работы которого в свою очередь стимулировали исследования Д. Валлиса. В 1663 году Валлис доказал постулат о параллельных, исходя из явного допущения, что для каждой фигуры существует подобная ей фигура произвольной величины. Это допущение он считал вытекающим из существа пространственных отношений.

С логической точки зрения результаты Хайяма или Валлиса лишь выявляли равносильность V постулата и некоторых других предложений геометрии. Так, Хайям, по существу, установил эквивалентность постулата и предложения о сумме углов треугольника, а Валлис показал, что не только из V постулата можно вывести учение о подобии, но и обратно – их евклидова учения о подобии следует V постулат.

Один из обнадеживающих способов подхода к доказательству пятого постулата, которым пользовались многие геометры XVIII и первой половины XIX веков, состоит в том, что пятый постулат заменяется его отрицанием или каким-либо утверждением, эквивалентным отрицанию. Опираясь на измененную таким образом систему постулатов и аксиом, доказываются всевозможные предложения, логически из нее вытекающие. Если пятый постулат действительно вытекает из остальных постулатов и аксиом, то измененная указанным образом система постулатов и аксиом противоречива. Поэтому рано или поздно мы придем у двум взаимно исключающим выводам. Этим и будет доказан пятый постулат.

Именно таким путем пытались доказать пятый постулат Д. Саккери (1667-1733), И. Г. Ламберт (1728-1777) и А.М. Лежандр (1752-1833).

Особенно оригинальна была попытка патера Джироламо Саккери (1667 – 1773), который основал свое доказательство на том логическом законе, что «из истинного положения нельзя ввести ложное следствие». Поэтому, принимая первые 28 предложений 1 книги Евклида, Саккери отвергает постулат Евклида, как ложные и старается вывести из этого предположения ложное следствие. Такого следствия он не нашел, но зато вывел целый ряд теорем, которые будут справедливы, если заменить постулат Евклида его отрицанием, т. е. ряд теорем геометрии, основанной на отрицании постулата Евклида.

Таким образом, стараясь доказать постулат Евклида, Саккери вывел из его отрицания целый ряд свойств геометрии не-Евклидовой.

Иоганн-Генрих Ламберт (1728 – 1777) в третьей части своей «Theorie der Parallellinien» излагает свои исследования, сходные с исследованиями Саккери, только Ламберт за основную фигуру берет четырехугольник с тремя прямыми углами, причем относительно четвертого угла им высказываются три гипотезы: прямого, тупого и острого угла.[1; стр. 24-26]

В результате проблема параллельных оставалась к началу XIX века неразрешенной и положение казалось безвыходным. Большой знаток вопроса венгерский математик Фаркаш Бояи в 1820 году писал своему сыну Яношу: “Молю тебя, не делай только и ты попыток одолеть теорию параллельных линий: ты затратишь на это все свое время, а предложения этого вы не докажете все вместе. Не пытайся одолеть теорию параллельных линий ни тем способом, который ты сообщаешь мне, ни каким-либо другим. Я изучил все пути до конца: я не встретил ни одной идеи, которой бы я не разрабатывал. Я прошел весь беспросветный мрак этой ночи, и всякий светоч, всякую радость жизни я в ней похоронил… Этот беспросветный мрак… никогда не прояснится на земле, и никогда несчастный род человеческий не будет владеть чем-либо совершенным даже в геометрии. Это большая и вечная рана в моей душе…”. Беспросветный мрак, о котором с горечью писал старший Бойяи, рассеял Лобачевский и, несколько позднее, Я. Бояи.

 

2 Опровержение пятого постулата Евклида

Гаусс обратился к теории параллельных в 1792 г. Сначала он надеялся доказать пятый постулат, но затем пришел к мысли о построении новой геометрии, которую назвал неевклидовой. В 1817 г. в одном из писем признался: "Я прихожу все более к убеждению, что необходимость нашей геометрии не может быть доказана". Но обнародовать эти идеи он не решился из боязни быть непонятым. Гаусс не опубликовал ни один из своих результатов, хотя из его писем и личных бумаг видно, что он разработал основные положения неевклидовой геометрии.

Творцом новой геометрии стал так же и венгерский математик Янош Больяй (1802 - 1860). В отличие от Гаусса он стремился распространить свои идеи, но большинство математиков тогда еще не были готовы их воспринять.

Результаты Яноша Больяя были сжато изложены в 1832 г. в приложении книге его отца, Фаркаша Больяя. Труд Я. Больяя "Приложение, содержащее науку о пространстве, абсолютно истинную, не зависящую от истинности или ложности XI аксиомы Евклида (что a priori никогда решено быть не может)" обычно кратко называют "Аппендикс" (от лат. "приложение"). Прочитав это сочинение, Гаусс написал своему ученику, математику Герлишу: "Я считаю молодого геометра фон Больяя гением первой величины". Однако в письме к Ф. Больяю он отозвался о сочинении Яноша гораздо сдержаннее: "Теперь кое-что о работе твоего сына. Если я начну с того, что эту работу не должен хвалить, то ты конечно, на мгновение поразишься, но иначе я не могу; хвалить ее значило бы хвалить самого себя: все содержание сочинения, путь, по которому твой сын прошел, и результаты, которые он получил, почти сплошь совпадают с моими собственными достижениями, которые частично имеют давность 30-35 лет". Не найдя поддержки у современников, Я. Больяй перестал заниматься математикой. Он умер в состоянии глубокой депрессии за несколько лет до того, как неевклидова геометрия получила всеобщее признание.

 

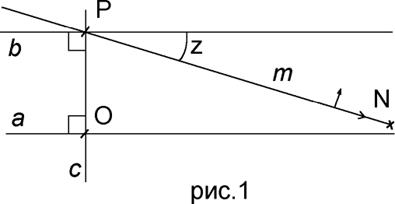
3 Основы геометрии Лобачевского

Исходным пунктом геометрии Лобачевского является принятие всех предложений геометрии Евклида, не зависящих от 5-го постулата (то есть абсолютной геометрии, включая аксиомы Паша, Архимеда, Дедекинда), и присоединение к ним взамен отброшенного 5-го постулата следующей аксиомы, противоположной аксиоме Плейфера, а значит, и 5-му постулату:

Через точку, лежащую вне прямой в плоскости, определяемой ими, можно провести не менее двух прямых, не пересекающих данную прямую.

Существование хотя бы одной прямой, проходящей через данную точку и не пересекающей данной прямой, есть факт абсолютной геометрии. Аксиома Лобачевского утверждает существование по крайней мере двух таких прямых. Отсюда немедленно следует, что таких прямых существует бесконечное множество.

Плоскость, в которой предполагается выполнение аксиомы Лобачевского, называется плоскостью Лобачевского.

Итак, имеем две прямые a и b лежащие в одной плоскости, пересеченные третьей прямой c (рис. 1). Углы при точках пересечения O и P данных прямых равны 90 градусам. Соответственно, сумма внутренних односторонних углов равна 180 градусам. Абсолютная геометрия, т.е. геометрия, не использующая пятый постулат Евклида в своих доказательствах, утверждает, что такие прямые не пересекутся.

Теперь построим прямую m проходящую через точку P и образующую с прямой b некоторый, сколь угодно малый, угол z. Таким образом мы получили две прямые a и m, пересеченные третьей прямой c, причем сумма одной из пар внутренних односторонних углов меньше 180 градусов на величину z. Лобачевский допустил, что существует некоторая величина z такая, что прямая m не пересечет прямую a, будучи как угодно далеко продленной.

Действительно, если поставить воображаемый эксперимент по продлению прямой m в направлении сближения с прямой a, можно заметить что, как только “отслеживаемая точка” N, движущаяся в воображении по прямой m, приблизиться к прямой a, мы всегда можем уменьшить величину угла z, и продолжить движение не пересекая прямую a. И так “до бесконечности”. Хотя это довольно профанирующий способ описания геометрии Лобачевского, причем только одного из ее ключевых моментов, но он позволяет несколько примирить сознание со столь не естественным для восприятия утверждением о том, что при таком построении прямые могут не пересечься.[7]

Приведенный выше способ апеллирует к невозможности верифицировать, или установить, момент пересечения прямых в конкретной точке, но Лобачевский исходил из несколько других предположений. А именно из того, что пятый постулат Евклида ни откуда не следует и является лишь нашим “ощущением” того, как должны вести себя прямые в случае пятого постулата. Соответственно Лобачевский не пытался объяснить, как прямые не пересекаются, а выдвинул утверждение, в ранге аксиомы, что существуют такие прямые, которые не пересекаются.

Основная теорема:

Пусть в плоскости даны прямая a и не лежащая на ней точка A. Тогда в пучке прямых с центром в точке A существуют две пограничные прямые, разделяющие все прямые пучка на два класса: на класс прямых, пересекающих a, и класс прямых, не пересекающих a. Эти граничные прямые сами не пересекают a.

Всё сказанное приводит нас к следующей картине расположения прямых пучка с центром в точке A, взятой вне данной прямой BB'. В этом пучке существуют две граничные прямые CC' и DD' (рис.2), симметрично расположенные относительно перпендикуляра AP, опущенного из точки A на BB', и образующие с ним ےCAP = ےD'AP = α<90°.

Эти прямые, а также все прямые пучка, проходящие внутри заштрихованных вертикальных углов CAD и C'AD', не пересекают прямой BB', а все прямые пучка, проходящие внутри вертикальных углов CAD' и C'AD, пересекают BB'.

Две граничные прямые CC' и DD' называются параллельными прямой BB' в точке A, причём прямая C'C называется параллельной B'B в направлении B'B, а прямая DD' называется параллельной прямой BB' в направлении BB'. Острый угол α, образуемый параллельными с перпендикуляром AP, называется углом параллельности в точке A относительно прямой BB'. Этот угол есть функция длины p перпендикуляра AP и обозначается так: α=П(p). AP называется отрезком параллельности в точке A относительно прямой BB'.

Основная формула геометрии Лобачевского, устанавливающая зависимость между длиной отрезка и отвечающим ему углом параллельности, имеет вид:

 

(*)

 

Все прямые пучка, не пересекающие BB' и лежащие внутри заштрихованных вертикальных углов, называются расходящимися с BB' или сверхпараллельными к BB'; угол, образуемый такой прямой с перпендикуляром AP с обеих от него сторон, больше угла параллельности α.

Наконец, все остальные прямые пучка, образующие с AP с какой-либо стороны острый угол, меньший угла параллельности α, называются пересекающими прямую BB' или сходящимися с BB'.

Определение. Прямая C'C называется параллельной прямой B'B в направлении B'B (рис.3) в точке A, если, во-первых, прямая C'C не пересекает прямой BB', во-вторых, C'C является граничной в пучке прямых с центром в точке A, то есть всякий луч AE, проходящий внутри угла CAD, где D – любая точка прямой BB', пересекающей луч DB.

Замечание. Из вышеизложенного ясно, что через точку A, лежащую вне прямой BB', можно провести в каждом из двух направлений лишь единственную параллельную Лобачевского к прямой BB', то есть каждому значению длины перпендикуляра p соответствует вполне определённое значение угла параллельности α. [5]

 

4 Сферическая геометрия

Геометрические построения и вычисления на поверхности сферы отличаются от таковых на плоскости. Поэтому можно говорить о сферической геометрии как о самостоятельном разделе геометрии.

Одними из основных понятий планиметрии являются понятия точки и прямой линии. В сферической геометрии аналогом прямой линии как линии с наименьшей длиной, соединяющей две точки, является дуга окружности, образованной пересечением большого круга с небесной сферой. Так как круг - это часть плоскости, ограниченная окружностью, то дадим следующее определение.

Определение 1 Большим кругом называется часть плоскости, которая проходит через центр сферы.

Определение 2 Любая плоскость, которая не проходит через центр сферы, называется малым кругом.

Через любые две точки, лежащие на поверхности сферы, можно провести большой круг. Это утверждение эквивалентно аксиоме из планиметрии: через любые две точки можно провести прямую линию. Перпендикуляр к большому кругу, проходящий через центр сферы, пересекает ее в двух точках, называемых полюсами. Большой круг пересекает сферу по окружности. Очевидно, что любая прямая, лежащая в плоскости большого круга и проходящая через центр сферы, является диаметром сферы. Следовательно, два больших круга пересекаются по диаметру сферы.

Рассмотрим сферу с центром в точке O (рис. 4).

Проведем большой круг через две точки A и B, лежащие на поверхности сферы, затем проведем перпендикуляр к большому кругу. Полюсы обозначим как P и Z. Через точки P и A, затем через P и B проведем два больших круга.

Определение 3 Угол между плоскостями двух больших кругов называется двугранным углом.

Единицами измерения углов в астрономии являются градусы, радианы, часы. Так как радиус сферы равен единице, то длина дуги (рис. 3) равна центральному углу AOB, то есть φ, выраженному в радианах.

Рассмотрим теперь три точки, которые лежат на сфере и не принадлежат одному большому кругу. Через каждую пару точек можно провести большие круги (рис. 5).

Определение 4 Сферическим треугольником называется фигура, образованная тремя дугами окружностей больших кругов, попарно соединяющих три точки.

Примерами сферических треугольников могут быть треугольники ABP, ABZ (рис. 4) и ABC (рис. 5).

Обычно углы сферического треугольника обозначают большими буквами, например A, B, C, а стороны, противолежащие углам - соответствующими малыми буквами: AB = c, BC = a, AC = b (рис. 5). Как и в планиметрии, в сферической геометрии существуют определенные соотношения между сторонами и углами треугольников. Отметим следующие свойства сферических треугольников. Углы A и B в треугольнике ABP (рис. 4) - прямые, так как большие круги, проходящие через точки P, A, Z и P, B, Z, перпендикулярны плоскости AOB. Поэтому, поскольку угол φ>0, сумма углов сферического треугольника может превышать 180°. Теперь проведем плоскость через точки A, B, C (рис. 5), лежащие на сфере, и параллельно ей плоскость, которая проходит через центр сферы. Очевидно, что эта плоскость поделит сферу на две полусферы, причем треугольник ABC будет полностью лежать в одной из полусфер. Таким образом, любой из углов сферического треугольника будет меньше, чем 180°. В пределе (при увеличении каждого из углов до 180°) сферический треугольник трансформируется в полусферу.

Следующие свойства сферического треугольника аналогичны свойствам плоского треугольника:
а) В каждом сферическом треугольнике против большего угла лежит большая сторона;
б) Сумма любых двух сторон больше третьей стороны.

Площадь сферического треугольника ABC (рис.6) равна

S = R²(A + B + C – π),

где углы A, B, C выражены в радианах. [6]

 

ЗАКЛЮЧЕНИЕ

 

Пятый постулат Евклида оставался недоказанным в течение двух тысяч лет. Многие знаменитые математики терпели неудачи, пытаясь его доказать. И только в начале позапрошлого века наш соотечественник Николай Иванович Лобачевский смог опровергнуть пятый постулат Евклида, дав начало новой, отличной от евклидовой, геометрии.

Геометрия Лобачевского продолжает разрабатываться многими геометрами; в ней изучаются: решение задач на построение, многогранники, правильные системы фигур, общая теория кривых и поверхностей и тому подобное. Ряд геометров развивали также механику в пространстве Лобачевского. Эти исследования не нашли непосредственных применений в механике, но дали начало плодотворным геометрическим идеям. В целом геометрия Лобачевского является обширной областью исследования, подобно геометрии Евклида.

Приложения геометрии Лобачевского. Сам Лобачевский применил свою геометрию к вычислению определённых интегралов. В теории функций комплексного переменного геометрия Лобачевского помогла построить теорию автоморфных функций. Связь с геометрией Лобачевского была здесь отправным пунктом исследований Пуанкаре, который писал, что "неевклидова геометрия есть ключ к решению всей задачи". Геометрия Лобачевского находит применение также в теории чисел, в её геометрических методах, объединённых под названием "геометрия чисел". Была установлена тесная связь геометрии Лобачевского с кинематикой специальной (частной) теории относительности.

Замечательное приложение геометрия Лобачевского нашла в общей теории относительности. Если считать распределение масс материи во Вселенной равномерным (это приближение в космических масштабах допустимо), то оказывается, что при определённых условиях пространство имеет геометрию Лобачевского. То есть, предположение Лобачевского о его геометрии как возможной теории реального пространства оправдалось.

 

список использованных источников

 

1 Иовлев Н.Н.

Введение в элементарную геометрию и тригонометрию Лобачевского.- Ленинград.: Государственное издательство,1930.-67

2 Клейн Феликс

Неевклидова геометрия.- М.- Ленинград.: Объединенное научно-техническое издательство НКТП СССР,1936.-356

3 Лобачевский Николай Иванович

Геометрические исследования по теории параллельных линий.- Ленинград.: «Полиграфкнига», 1945.-176

4 Смогоржевский Александр Степанович

О геометрии Лобачевского.- М.: Государственное издательство технико-теоретической литературы,1957.-68

5 www.geom.kgsu.ru – Геометрия Лобачевского

6 www.astronet.ru – Российская астрономическая сеть

7 www-k.narod.ru – Пятый постулат Евклида

 

 

ПРИЛОЖЕНИЕ

 

Рисунки

 

 

Рис. 2

 

 

Рис.3

 

 

 

Рис. 4 Определение двугранного угла

 

 

 

 

Рис 5 Определение сферического треугольника

 

 

 

Рис. 6 Вычисление площади сферического треугольника