Задача 1. Исследование плоского напряженного состояния в точке. Определение напряжений и деформаций в заданном направлении
Если вы обнаружили у себя хотя бы 2-3 из вышеперечисленных признаков, то вам необходимо принимать ТАБЛЕТКИ РАСТОРОПШИ с СОЛЯНКОЙ ХОЛМОВОЙ. Если вы не обнаружили у себя такие признаки, принимайте ихдля профилактики подобных состояний.
БАД «ТАБЛЕТКИ РАСТОРОПШИ с СОЛЯНКОЙ ХОЛМОВОЙ» можно принимать как самостоятельно, так и в комплексе с другими продуктами. О других вариантах применения данного продукта читайте в материале «ПРОГРАММЫ ЗДОРОВЬЯ TianDe». Берегите себя и будьте здоровы! Задача 1. Исследование плоского напряженного состояния в точке. Определение напряжений и деформаций в заданном направлении Главные напряжения - напряжения на главных площадках. Главные площадки – площадки, на которых касательные напряжения обращаются в ноль, а нормальные принимают экстремальные значения. Площадка сдвига – площадка, на которой касательные напряжения принимают экстремальные значения. Площадка чистого сдвига – площадка, на которой касательные напряжения принимают экстремальные значения, а нормальные отсутствуют. Угол между главной площадкой и площадкой сдвига составляет 45°. Угол α0 между исходной и главной площадкой определяется с помощью формулы:
Угол между исходной и главной площадкой находится в интервале 0≤α0≤45°. Правило знаков для нормальных напряжений: «+» при растяжении, «-» при сжатии, а для касательных зависит от направления: «+» по ходу часовой стрелки, «-» против хода. Главные напряжения: σ1, σ2, σ3, индексы 1, 2 и 3 присваивают в следующем порядке σ1>σ2>σ3. Различают три типа напряженного состояния: линейное (одно из главных напряжений отлично от нуля), плоское (два главных напряжения отличны от нуля), объемное или пространственное (все три главных напряжения отличны от нуля). Определить главные напряжения можно с помощью зависимости (2):
Правильность результатов расчета проверяют с помощью первого инварианта тензора напряжений, который для плоского напряженного состояния (σz=0) имеет вид: σmax+σmin= σx+σy. Затем главным напряжениям присваивают индексы опираясь на то, что σ1>σ2>σ3. Например: 10>0>-5, тогда σ1=10, σ2=0, σ3=-5, или 0>-10>-30, в этом случае σ1=0, σ2=-10, σ3=-30, или 40>10>0 здесь σ1=40, σ2=10, σ3=0. Касательные напряжения на площадке сдвига определяют по зависимости:
Гипотезы прочности можно представить в следующем виде: III гипотеза прочности IV гипотеза прочности Напряжения на площадке повернутой на угол α относительно исходной площадки можно определить по следующим зависимостям:
Деформации в направлении главных напряжений называют главными деформациями и находят их значения по зависимостям:
Пример выполнения индивидуального задания
Дано: σx=80МПа, σy=20МПа, τyx=40МПа, α=35°, ν=0,28, Е=2,06×105МПа, R=240МПа.
Требуется: 1. Определить знаки заданных напряжений. 2. Определить величины и направления главных напряжений, изобразить главные площадки. 3. Вычислить максимальные 4. Определить нормальные и касательные напряжения на площадке, повернутой относительно заданной на угол 5. Выполнить проверку прочности по 3-й и 4-й гипотезе прочности. 6. Определить относительные деформации по направлению главных напряжений. Решение 1. Определение знаков напряжений: 2. Определение величины и направления главных напряжений с помощью (2):
Выполним проверку, используя первый инвариант напряжений σmax+σmin= σx+σy 100+0=80+20 0=0 верно. Присвоим индексы главным напряжениям, опираясь на зависимость σ1>σ2>σ3.
Определим угол между главной площадкой и исходной по зависимости (1):
Т.к. угол α0 отрицательный, значит, поворот площадки при переходе от исходной к главной площадке осуществляется по ходу часовой стрелки. Выполним чертеж.
При выполнении чертежа необходимо выполнить следующее. Максимальное главное напряжение (σ1) должно быть ближе к алгебраически наибольшему из исходных напряжений (в данном случае σx), а также располагаться в той четверти, где сходятся исходные касательные напряжения. Минимальное главное напряжение (σ3) должно быть ближе к алгебраически наименьшему из исходных напряжений (здесь σy). Тоже можно сформулировать следующим образом. За точку отсчета принимают алгебраически наибольшее из исходных напряжений, затем поворачивают площадку по направлению исходного касательного напряжения и получают местоположение максимального из главных напряжений. 3. Определение максимальных касательных напряжений производят с помощью зависимости (3), вывод которой представлен ниже. За исходную площадку принимают главную, поэтому вместо напряжений σx и σy в формуле используют главные напряжения, располагающиеся на площадке, в этой задаче σ1 и σ3. Касательное напряжение
Нормальные напряжения на этой площадке определяются как
Выполним проверку σα+45°+σα-45°= σx+σy 50+50=80+20
При выполнении чертежа необходимо учесть, что максимальные и минимальные касательные напряжения сходятся у σ1. 4. Определим нормальные и касательные напряжения на площадке, повернутой относительно заданной на угол
Нормальные напряжения получились положительные, значит растягивающие, и касательное, тоже положительное, значит, на чертеже будет изображено по ходу часовой стрелки.
Определим полное напряжение на наклонной площадке
и относительную деформацию в направлении напряжения σα
5. Определим значения расчетных сопротивлений и выполним проверку прочности по 3-й и 4-й гипотезе прочности
6. Определим относительные деформации по направлению главных напряжений. Для этого воспользуемся зависимостями (5)
Знак плюс говорит о растяжении и увеличении размеров, минус о сжатии и уменьшении.
|


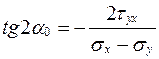 . (1)
. (1)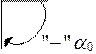
 Правило знаков для угла α0 следующее.
Правило знаков для угла α0 следующее. . (2)
. (2)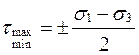 . (3)
. (3) ,
, .
. (4)
(4) (5)
(5)
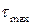 и минимальные
и минимальные  касательные напряжения и их направления, изобразить площадки, на которых они действуют. Определить на этих площадках
касательные напряжения и их направления, изобразить площадки, на которых они действуют. Определить на этих площадках  и
и  .
. . Показать эту площадку и напряжения на ней. Определить полное напряжение на этой площадке и относительную деформацию по направлению
. Показать эту площадку и напряжения на ней. Определить полное напряжение на этой площадке и относительную деформацию по направлению 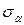 .
. =20МПа (растяжение),
=20МПа (растяжение),  =40МПа (по ходу часовой стрелки).
=40МПа (по ходу часовой стрелки). .
. .
. . Судя по количеству главных напряжений отличных от нуля это линейное напряженное состояние.
. Судя по количеству главных напряжений отличных от нуля это линейное напряженное состояние.


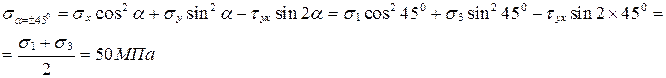
 0=0 верно.
0=0 верно.


 .
. ,
,




