Алгоритм сжатия с использованием кодов Хаффмана
Данный алгоритм (далее для краткости - алгоритм Хаффмана) был разработан в 1952 году и относится к группе статистических методов сжатия. Статистические методы используют различные приёмы для того, чтобы наиболее часто встречающимся символам соответствовали более короткие коды. При этом каждый код однозначно соответствует конкретному символу. Например, в тексте на русском языке буква а встречается гораздо чаще, чем буква ы, поэтому имеет смысл присвоить букве а более короткий код. Соответственно выходной поток этих методов является бит-ориентированным, т.е. не форматированным по границам байтов. Статистические методы работают медленнее словарных, но достигают, как правило, более высокой степени сжатия. Они используют три основных модели для набора статистики (определения вероятностей символов): - неадаптивную; - полуадаптивную; - адаптивную.
В неадаптивных моделях вероятности всех символов алфавита определены заранее. Эта модель обычно применяется только при сжатии текстовых файлов. В полуадаптивных моделях входные данные обрабатываются за 2 прохода: 1-й – для подсчёта вероятностей, 2-й – собственно для сжатия. Эта модель может применяться для сжатия не очень больших изображений. Адаптивные модели вычисляют и корректируют вероятности символов в процессе сжатия, т.е. «на лету». Модели последнего типа сложнее предыдущих, зато являются более универсальными и часто дают наилучшее сжатие. Рассмотрим кодирование по Хаффману более подробно. Предположим, что вероятности (их заменят частоты) всех символов алфавита уже подсчитаны одним из вышеописанных способов. Тогда: 1. Выписываем в ряд все символы алфавита в порядке убывания вероятноcтей (частоты) их появления в потоке данных (для удобства построения дерева); 2. Объединяем два символа с наименьшими вероятностями в новый составной символ, вероятность которого определяется как сумма вероятностей составляющих его символов. Последовательно повторяем эту операцию до образования единственного составного символа (корня). В результате получается дерево символов, каждый узел которого имеет суммарную вероятность всех объединённых им узлов. 3. Прослеживаем путь от каждого листа дерева к корню, помечая направление движения к каждому узлу (например, вверх/направо –1, вниз/налево - 0). При этом не важен конкретный вид разметки «ветвей» дерева (т.е. помечать направление вверх/направо –1, вниз/налево – 0, или наоборот), но важно придерживаться выбранного способа разметки ко всем «ветвям» дерева. 4. Получившиеся двоичные комбинации, записанные от конца к началу и формируют коды Хаффмана.
Полученный коэффициент сжатия подсчитывается по следующей формуле
где n – количество бит, необходимое для кодирования символов алфавита фиксированным числом разрядов;
Коды Хаффмана никогда не увеличивают, а чаще всего наоборот, уменьшают среднюю длину кодовых слов для символов в цепочке данных. Поэтому сжатие с применением кодов Хаффмана, всегда имеет коэффициент ³ 1, причём знак равенства получается только в том случае, когда вероятности всех символов во входном потоке одинаковы. Пример кодирования по Хаффману приведен на рис. 3.
Примечание: 1) для удобства расчётов при выполнении практической части, дробное значение частоты символа можно заменить целым числом появлений данного символа в цепочке, поэтому в корне дерева получится не 1 (сумма частот), а значение, равное длине цепочки. В этом случае коэффициент сжатия рассчитывается по формуле
где K – общее количество символов во входном потоке;
2) частоты появления символов в примере расположены не по убыванию исключительно ради наглядности внешнего вида «дерева», т.к. в противном случае ветви пересекались бы между собой. Несмотря на то, что коды Хаффмана в обоих случаях могут отличаться, это не имеет значения, поскольку сохранится свойство однозначности кодов Хаффмана, т.е. ни один из кодов не совпадет с начальными битами другого, более длинного кода.
Рис.3. Пример кодирования по Хаффману.
Если предположить, что входной поток символов был байт-ориентированным, то n =8. Тогда коэффициент сжатия
Если считать входной поток символов бит-ориентированным с равным количеством бит под каждый символ, то n =4 (т.к. для кодирования 10 различных символов a-j требуется
Кодирование по Хаффману может использоваться при сжатии изображений как самостоятельно, так и в составе других алгоритмов сжатия, например LZW и JPEG (это наиболее эффективное его применение).
Контрольные вопросы
1. В чем отличие растровых и векторных форматов хранения данных? 2. Что такое палитра и в каких случаях она применяется? 3. Что такое информационная избыточность и каких видов она бывает? 4. В каких случаях коэффициент сжатия оказывается меньше единицы? 5. Что необходимо для эффективного сжатия по алгоритму LZW? 6. Может ли кодирование по Хаффману дать
|

 , (2)
, (2) - вероятность (частота) повторения символа
- вероятность (частота) повторения символа  во входном потоке;
во входном потоке; - количество бит в коде Хаффмана для символа
- количество бит в коде Хаффмана для символа  , (3)
, (3) – количество символов
– количество символов 

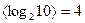 разряда). В этом случае
разряда). В этом случае 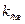 будет означать выигрыш, полученный от применения кодов Хаффмана по сравнению с кодами фиксированной, минимально необходимой битовой размерности. В этом случае
будет означать выигрыш, полученный от применения кодов Хаффмана по сравнению с кодами фиксированной, минимально необходимой битовой размерности. В этом случае
 ? Почему?
? Почему?


