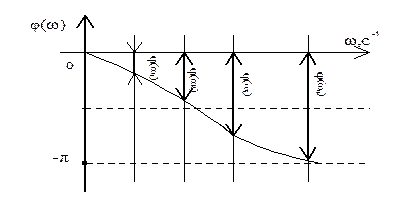Получение АЧХ и ФЧХ
Получение АЧХ и ФЧХ
Теперь рассмотрим частотные характеристики, которые получают при рассмотрении вынужденных движений системы, вызванных гармоническим воздействием на входе Изменение амплитуды и фазовый сдвиг являются функциями частоты и выражают динамические свойства элемента (системы). Если изменять частоту входных колебаний от 0 до ∞ и определять установившиеся амплитуду и фазу выходных колебаний для разных частот, можно получить зависимость соотношения амплитуд Проведение такого исследования можно представить, например, так (рис. 8.1): в трубопровод подачи топлива вмонтирована дроссельная заслонка, которую можно открывать и закрывать с определенной частотой при помощи специального механизма. При этом можно обеспечить синусоидальное изменение расхода топлива, являющегося входной величиной Таким образом, для каждой частоты входного сигнала (расхода газа) будут получены определенные амплитуда и фазовый сдвиг выходного сигнала (температуры в печи).
Рис. 8.1. Схема экспериментального определения частотных характеристик
Рис. 8.2. Входной и выходной сигналы в установившемся режиме
Если изобразить зависимость отношения амплитуд от частоты, получим АЧХ (построение показано на рис. 8.3. У обычных инерционных звеньев АЧХ по мере увеличения частоты падает. Хотя АЧХ теоретически продолжается до бесконечности, практическое значение имеет полоса пропускания, т.е. диапазон частот, в котором амплитуда колебаний выходного сигнала составляет не менее 5 % амплитуды колебаний входного сигнала. Если у АЧХ звена имеется максимум при Изобразив на графике зависимость фазового сдвига от частоты (построение на рис. 8.4), получим ФЧХ. Фазовая характеристика у обычных инерционных звеньев отрицательна, т.е. выходные колебания отстают по фазе от входных, причем это отставание увеличивается с ростом частоты.
Рис. 8.3. Построение амплитудно-частотной характеристики (АЧХ)
Рис. 8.4. Построение фазовой частотной хаврактеристики (ФЧХ)
|

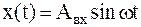 , где
, где  – амплитуда;
– амплитуда; 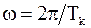 – угловая частота входных колебаний с периодом
– угловая частота входных колебаний с периодом  . Если
. Если  , то входное воздействие – единичное гармоническое. По окончании переходного процесса на выходе линейной системы устанавливаются гармонические колебания
, то входное воздействие – единичное гармоническое. По окончании переходного процесса на выходе линейной системы устанавливаются гармонические колебания  той же частоты, но с другой амплитудой и сдвинутые по фазе относительно входных колебаний на угол
той же частоты, но с другой амплитудой и сдвинутые по фазе относительно входных колебаний на угол  .
. от частоты – амплитудно-частотную (АЧХ) и сдвига фазы
от частоты – амплитудно-частотную (АЧХ) и сдвига фазы  – фазовую частотную (ФЧХ).
– фазовую частотную (ФЧХ). . Если измерять температуру в печи – выходной сигнал
. Если измерять температуру в печи – выходной сигнал  , то увидим, что в установившемся режиме она будет изменяться с той же частотой, а максимумы и минимумы расхода и температуры по фазам будут сдвинуты (рис. 8.2).
, то увидим, что в установившемся режиме она будет изменяться с той же частотой, а максимумы и минимумы расхода и температуры по фазам будут сдвинуты (рис. 8.2).

 , то соответствующую частоту называют резонансной.
, то соответствующую частоту называют резонансной.