Конечное решение
Нецелочисленное решение имеет вид: x 1опт= Выбираем решение с наименьшей целой частью. x 1= Очевидно, что меньшую целую часть имеет решение х 1 – целая часть равна единице. Для решения с наименьшей целой частью x 1= х 1+ Формируем правильное отсечение с учетом того, что дробная часть при x 1 равна нулю. { или
На 3-ем этапе правильное отсечение приводим к каноническому виду посредством введения в уравнение дополнительной неотрицательной целочисленной переменной х 5:
Это уравнение включаем в исходную систему ограничений, причем х 5 будет третьей базовой переменной. На 4-ом этапе решаем задачу симплекс-методом (таблица 4.4). Таблица 4.4 Исходная таблица для новой системы ограничений
Для этого случая, не обращая внимания на отрицательность оценок Приравнивая свободные переменные к нулю, получим недопустимое базисное решение ( Таблица 4.5
|
)
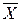; х 2опт= 
; fmax (
(умножим на «-1»).
; х 2= 
.
х 3- 
х 4= 
{ 
x 2
-2/5
и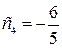 
, выбираем в качестве разрешающего столбца – столбец х 3 (или х 4), а в качестве разрешающей строки – строку х 5, чтобы исключить дополнительную переменную х 5 из дальнейшего рассмотрения.
